As a quick summary (read the paper and sequence if you want more details), they show that for any distribution over reward functions, if there are more "options" available after action 1 than after action 2, then most of the orbit of the distribution (the set of distributions induced by applying any permutation on the MDP, which thus permutes the initial distribution) has optimal policies that do action 1.
That is not what the theorems in the paper show at all (it's not just a matter of details). The relevant theorems require a much stronger and more complicated condition than having more "options" after action 1 than after action 2. They require the existence of an involution between two sets of real vectors where each vector corresponds to a "state visitation distribution" of a different policy.
To demonstrate that this is not just a matter of "details": Your description suggests that generally there is no problem to apply the theorems in stochastic environments (the paper deals with stochastic MDPs). But since the actual condition is much stronger than what you described here, the theorems almost never apply in stochastic environments!
It's usually impossible to construct a useful involution, as required by the theorems, in stochastic environments. The paper (and the accompanying posts) use the Pac-Man environment as an example, which is a stochastic environment. But the reason that the theorems can apply there a lot is that usually that environment behaves deterministically. The ghosts always move deterministically unless they are in "blue mode" (i.e. when they can't kill Pac-Man) in which they sometimes move randomly. This arbitrary quirk of the Pac-Man environment is what allows the theorems to show that "Blackwell optimal policies tend to avoid immediately dying in Pac-Man" as the paper claims. (Whenever Pac-Man can immediately die, the ghosts are not in "blue mode" and thus the environment behaves deterministically).
(I elaborated more on this here).
The point of using scare quotes is to abstract away that part. So I think it is an accurate description, in that it flags that “options” is not just the normal intuitive version of options.
So I think it is an accurate description, in that it flags that “options” is not just the normal intuitive version of options.
I think the quoted description is not at all what the theorems in the paper show, no matter what concept the word "options" (in scare quotes) refers to. In order to apply the theorems we need to show that an involution with certain properties exist; not that <some set of things after action 1> is larger than <some set of things after action 2>.
To be more specific, the concept that the word "options" refers to here is recurrent state distributions. If the quoted description was roughly correct, there would not be a problem with applying the theorems in stochastic environments. But in fact the theorems can almost never be applied in stochastic environments. For example, suppose action 1 leads to more available "options", and action 2 causes "immediate death" with probability 0.7515746, and that precise probability does not appear in any transition that follows action 1. We cannot apply the theorems because no involution with the necessary properties exists.
You're being unhelpfully pedantic. The quoted portion even includes the phrase "As a quick summary (read the paper and sequence if you want more details)"! This reads to me as an attempted pre-emption of "gotcha" comments.
The phenomena you discuss are explained in the paper (EDIT: top of page 9), and in other posts, and discussed at length in other comment threads. But this post isn't about the stochastic sensitivity issue, and I don't think it should have to talk about the sensitivity issue.
The phenomena you discuss are explained in the paper (EDIT: top of page 9), and in other posts, and discussed at length in other comment threads. But this post isn't about the stochastic sensitivity issue, and I don't think it should have to talk about the sensitivity issue.
I noticed that after my previous comment you've edited your comment to include the page number and the link. Thanks.
I still couldn't find in the paper (top of page 9) an explanation for the "stochastic sensitivity issue". Perhaps you were referring to the following:
randomly generated MDPs are unlikely to satisfy our sufficient conditions for POWER-seeking tendencies
But the issue is with stochastic MDPs, not randomly generated MDPs.
Re the linked post section, I couldn't find there anything about stochastic MDPs.
For (3), environments which "almost" have the right symmetries should also "almost" obey the theorems. To give a quick, non-legible sketch of my reasoning:
For the uniform distribution over reward functions on the unit hypercube (), optimality probability should be Lipschitz continuous on the available state visit distributions (in some appropriate sense). Then if the theorems are "almost" obeyed, instrumentally convergent actions still should have extremely high probability, and so most of the orbits still have to agree.
So I don't currently view (3) as a huge deal. I'll probably talk more about that another time.
That quote does not seem to mention the "stochastic sensitivity issue". In the post that you linked to, "(3)" refers to:
- Not all environments have the right symmetries
- But most ones we think about seem to
So I'm still not sure what you meant when you wrote "The phenomena you discuss are explained in the paper (EDIT: top of page 9), and in other posts, and discussed at length in other comment threads."
(Again, I'm not aware of any previous mention of the "stochastic sensitivity issue" other than in my comment here.)
The phenomena you discuss are explainted in the paper, and in other posts, and discussed at length in other comment threads.
I haven't found an explanation about the "stochastic sensitivity issue" in the paper, can you please point me to a specific section/page/quote? All that I found about this in the paper was the sentence:
Our theorems apply to stochastic environments, but we present a deterministic case study for clarity.
(I'm also not aware of previous posts/threads that discuss this, other than my comment here.)
I brought up this issue as a demonstration of the implications of incorrectly assuming that the theorems in the paper apply when there are more "options" available after action 1 than after action 2.
(I argue that this issue shows that the informal description in the OP does not correctly describe the theorems in the paper, and it's not just a matter of omitting details.)
As a quick summary (read the paper and sequence if you want more details), they show that for any distribution over reward functions, if there are more "options" available after action 1 than after action 2, then most of the orbit of the distribution (the set of distributions induced by applying any permutation on the MDP, which thus permutes the initial distribution) has optimal policies that do action 1.
Also, this claim is missing the "disjoint requirement" and so it is incorrect even without the "they show that" part (i.e. it's not just that the theorems in the paper don't show the thing that is being claimed, but rather the thing that is being claimed is incorrect). Consider the following example where action 1 leads to more "options" but most optimal policies choose action 2:
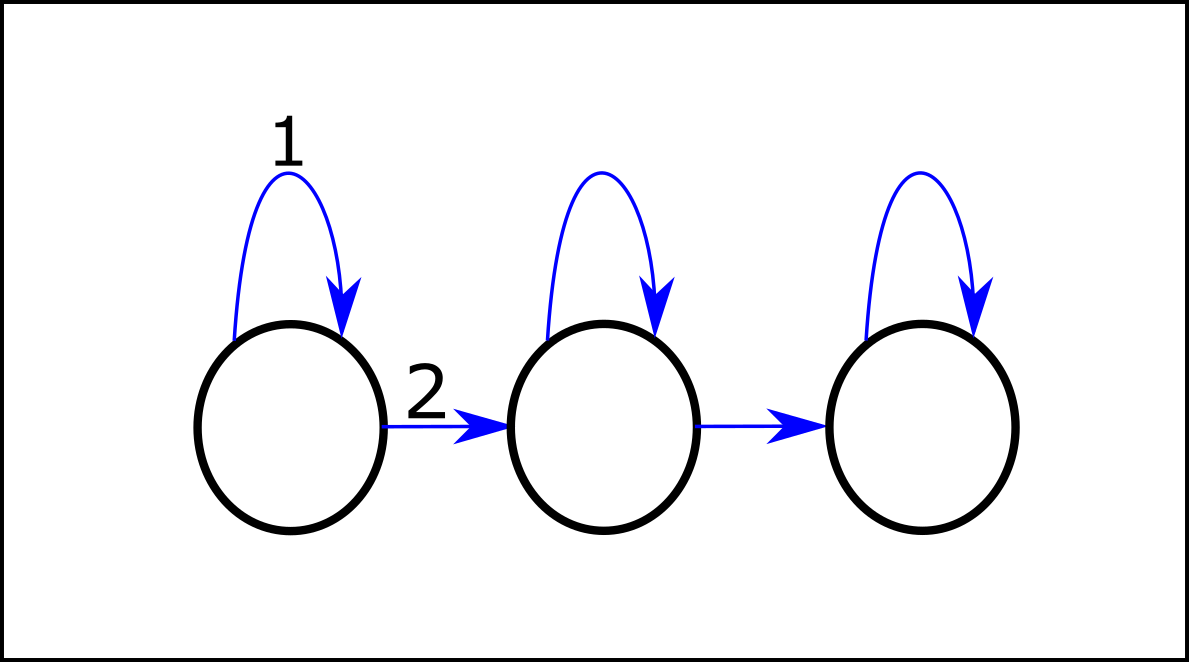
From single choice to successive choices
Alex Turner (and collaborators) have done a great work deconfusing instrumental convergence for a single choice. As a quick summary (read the paper and sequence if you want more details), they show that for any distribution over reward functions, if there are more "options" available after action 1 than after action 2, then most of the orbit of the distribution (the set of distributions induced by applying any permutation on the MDP, which thus permutes the initial distribution) has optimal policies that do action 1.
(A subtlety that matters is the meaning of optimal here: the result applies for all distributions only for average-step reward, which never cares about transient rewards and only value what happens in the loops. That being said, the distributions for which this doesn't generalize to Blackwell optimality are a a set of zero measure -- where Blackwell optimality is the "classic" RL notion of optimality with discount factor close to 1, which thus takes into account transient rewards)
So it's not so much telling us something about a specific distribution over reward functions (which may incentivize the action with less options) but about its orbit. It's giving teeth to the fragility of value with regard to instrumental convergence: we have to hit a target in the orbit that represents less than half of it.
Alex's recent combinatorial generalizations considerably strengthen this point: if action 1 allows n times more options than action 2, at least nn+1 of the orbit has optimal policies taking action 1.
For big enough n, the target to hit for no instrumental convergence shrinks to vanishingly small.
In this post, I adapt these result for the case of successive choices: what is the proportion of the orbit for which it is optimal to take the first k instrumental convergent choices? In addition to symmetry, additional information is required, in the form of the intersection of the sets of options for successive non-instrumentally convergent choices.
(Note: technically power-seeking and instrumental convergence are slightly different, but I'll use the more common -- in this context -- power-seeking by simplicity)
Thanks to Alex Turner for answering my many questions, pointing out a problem in a previous draft, and for all the work that gave me the tools for this little contribution.
Two examples
Can we directly apply the power-seeking theorems for every single choice, and then combine them somehow to get power-seeking results for successive choices? Phrased differently, are the ratios for each single choice sufficient statistics to compute the ratios for successive choices?
In some cases, we need more. To see that, let's start with a simple example.
The is the easy case, when no additional information is needed. Applying the combinatorial results to the first choice leads to 34 of the orbit with optimal policies (for average-step reward; see Subtleties section for the case of Blackwell optimality) going right, and applying them to the second choice (after going right initially) leads to 23 of the orbit with optimal policies going right.
Note that this second number would be the same if the MDP started at this second choice directly -- only the "possible futures" matter here. This then tells us that, of the at least 34 of the orbit that goes right at the first choice, there is then at least 23 going right. Hence the successive ration is simply the product of the previous ratios (34.23=12); and that for as many successive power-seeking choices as we want in this context.
Notably, this means that there are as much orbit element who take the two power-seeking choices as there are who don't do that (so take either none or just the first one). And that despite the ratio of 23 for the second power-seeking choice!
Let's see with another example why this is not always how it works.
the difference with the previous graph is that the non-power-seeking option is shared.
There is a single difference with the other graph: the two non-power-seeking options both lead to the same option that I shall call "death", because a death state is a good example of a single state that can be reached in numerous ways.
First impact of this change: the first choice now has also a ratio of 1, because the death state is an available option for both actions. Since average-step optimality only cares about the final loop, optimal policies that want to reach the death state can do so by any mean. Hence no orbit element forbids its optimal policy to go right.
What happens for the next power-seeking choice? Here, death is only accessible on the left; we thus just apply the normal power-seeking theorems to get at least 23of the orbit arriving at this choice going left.
We get the successive ratio by a product, just like in the previous case. But notice that despite having two choices, we only felt the impact of one. And despite the number of options on each side being the same between the two examples, the ratio in the second case in 23 instead of 12.
Note that adding intermediary power-seeking choices with only the shared death state as the non-power-seeking option wouldn't have changed the successive ratio.
Subtleties
Of course, the situation is not always as simple as those two extremes. Here are some additional subtleties to consider:
Maybe these two problems cancel each other: maybe the distributions for which the combinatorial result apply are the ones which break the argument above (or at least contains the latter).
But for the moment, this needs further work.
Conclusion: Disjointness in addition to symmetry
If what I've been writing is correct (which can only really be checked by a clean math proof that I'll do at some point), then we need another graphical information, in addition to symmetry, to go from single choice power-seeking analysis to the successive choices case: whether the non-power-seeking options are disjoint over successive choices.
I'm quite excited about that, because even if the condition becomes slightly more involved, it still relies on a graphical and intuitive criteria.