This is Part 3a of my «Boundaries» Sequence on LessWrong.
Here I attempt to define (organismal) boundaries in a manner intended to apply to AI alignment and existential safety, in theory and in practice. A more detailed name for this concept might be an approximate directed (dynamic) Markov blanket.
Skip to the end if you're eager for a comparison to related work including Scott Garrabrant's Cartesian frames, Karl Friston's active inference, and Eliezer Yudkowsky's functional decision theory; these are not prerequisites.
Motivation
In Part 3b, I'm hoping to survey a list of problems that I believe are related, insofar as they would all benefit from a better notion of what constitutes the boundary of a living system and a better normative theory for interfacing with those boundaries. Here are the problems:
- AI boxing / Containment — the method and challenge of confining an AI system to a "box", i.e., preventing the system from interacting with the external world except through specific restricted output channels (Bostrom, 2014, p.129).
- Corrigibility — the problem of constructing a mind that will cooperate with what its creators regard as a corrective intervention (Soares et al, 2015).
- Mild Optimization — the problem of designing AI systems and objective functions that, in an intuitive sense, don’t optimize more than they have to (Taylor et al, 2016).
- Impact Regularization — the problem of formalizing "change to the environment" in a way that can be effectively used as a regularizer penalizing negative side effects from AI systems (Amodei et al, 2016).
- Counterfactuals in Decision Theory — the problem of defining what would have happened if an AI system had made a different choice, such as in the Twin Prisoner's Dilemma (Yudkowsky & Soares, 2017).
- Mesa-optimizers — instances of learned models that are themselves optimizers, which give rise to the so called inner alignment problem (Hubinger et al, 2019).
- Preference Plasticity — the possibility of changes to the preferences of human preferences over time, and the challenge of defining alignment in light of time-varying preferences (Russell, 2019, p.263).
- (Unscoped) Consequentialism — the problem that an AI system engaging in consequentialist reasoning, for many objectives, is at odds with corrigibility and containment (Yudkowsky, 2022, no. 23).
Also, in the comments after Part 1 of this sequence, I asked commenters to vote on which of the above 8 topics I should write a deeper analysis on; here's the current state of the vote:
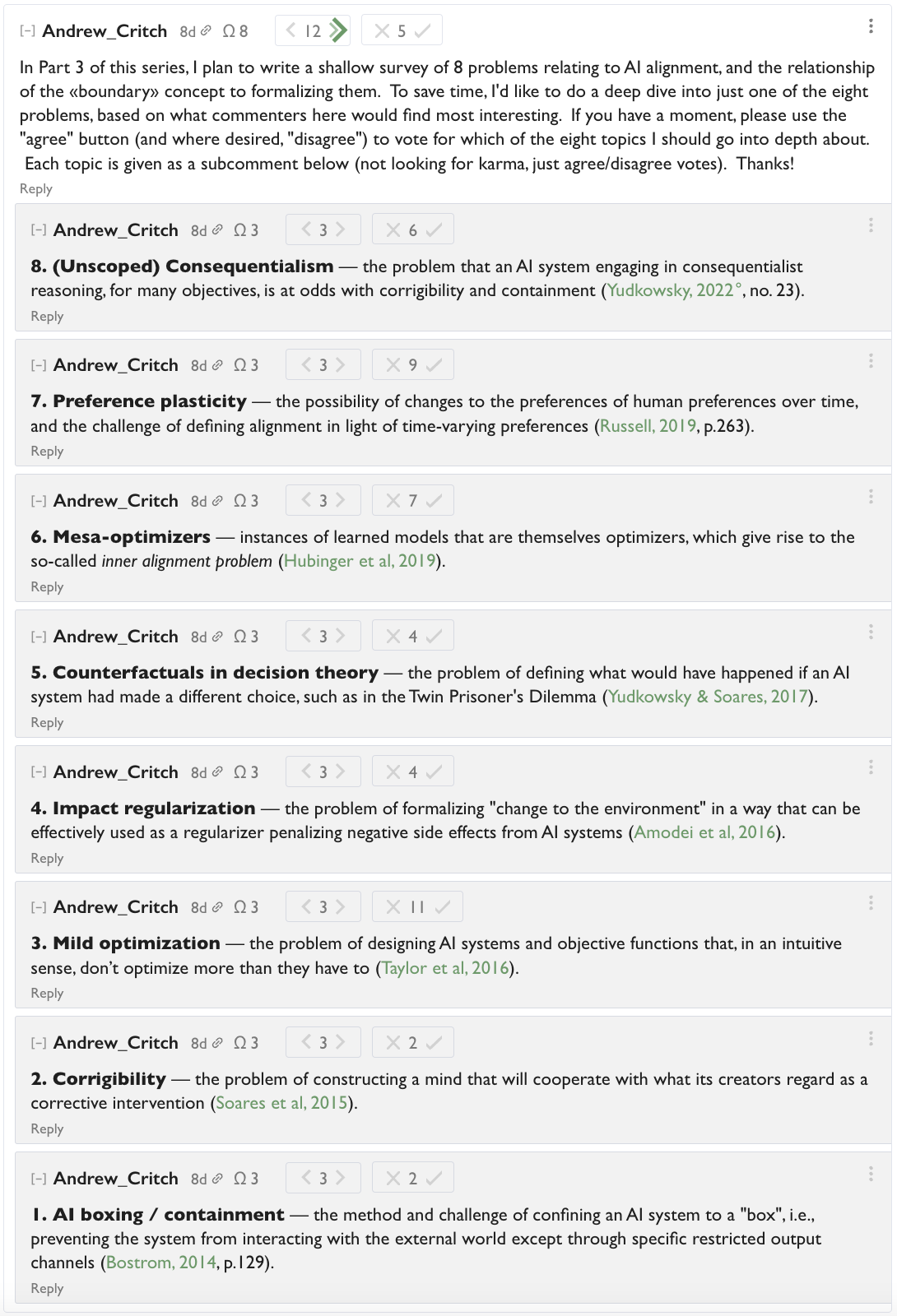
Go cast your vote, here! Or read this part first and then vote :)
Boundaries, defined
Boundaries include things like a cell membrane, a fence around yard, and a national border; see Part 1. In short, a boundary is going to be something that separates the inside of a living system from the outside of the system. More fundamentally, a living system or organism will be defined as
- a) a part of the world, with
- b) a subsystem called its boundary which approximately causally separates another subsystem called its viscera from the rest of the world,
where - c) the boundary state decomposes into active and passive features that direct causal influence outward and inward respectively, such that
- d) the boundary and viscera together implement a decision-making process that perpetuates these four defining properties.
One reason this combination of properties is interesting is that systems that make decisions to self-perpetuate tend to last longer and therefore be correspondingly more prevalent in the world; i.e., "survival of the survivalists".
But more importantly, this definition will be directly relevant both to x-risk and to individual humans. In particular, we want the living system called humanity to use its model of itself to perpetuate its own existence, and we want AI to be respectful of that and hopefully even help us out with it. It might seem like continuing our species is just an arbitrary subjective preference among many that humanity would espouse. However, I'll later argue that the preservation of boundaries is a special kind of preference that can play a special role in bargaining, due to having a (relatively) objective or intersubjectively verifiable meaning.
To get started, let's expand the concise definition above with more mathematical precision, one part at a time. Eventually my goal is to unpack the following diagrams:
Definition part (a): "part of the world"
First, let's define what it means for the living system boundary to be a part of the world. For that, let's represent the world as a Markov chain (definition:Wikipedia), which intuitively just means the future only depends on the past via the present.
- the set of possible fully-detailed states of the entire world, including all details of the world, which will include the living system in question, and its boundary. A world state is not a compressed or simplified model of the world the agent lives in; it's a fully detailed description of the entire world.
- is the set of all possible sequences of world states, i.e., complete world histories. In future work we can add a parameter for the resolution of time steps, but I don't think that's crucial here.
- is a (stochastic) transition function, defining the probability that the world will transition to state in the next time step, given that it is in state . By modeling the world as a linear time series like this, I'm knowingly omitting considerations of special relativity (where time is relative), general relativity (where time is curved), a quantum mechanics (where wave amplitudes are more fundamental than probabilities). I don't think any of these omissions render useless the concept of boundaries developed here.
- is a specified initial distribution on worlds at the start of time or earliest time of interest (), which defines a distribution over all possible histories from that time forward.
- is the natural map which, given a distribution over world states , returns a distribution over futures obtained by repeated application of over time.
- denotes, for any world state , the future of the Dirac (100% concentrated) distribution on the world state .
- denotes the distribution over futures by in the initial distribution .
- is the state of the world at time , as a random variable, obtained by projecting onto its component,
- is the sequence of states of the world prior to time (as a random variable).
- is the sequence of states of the world after time .
Since the world at each time is generated purely from the previous moment in time, it follows that history satisfies the temporal Markov property: . In other words, the future is independent of the past, conditional on the present.
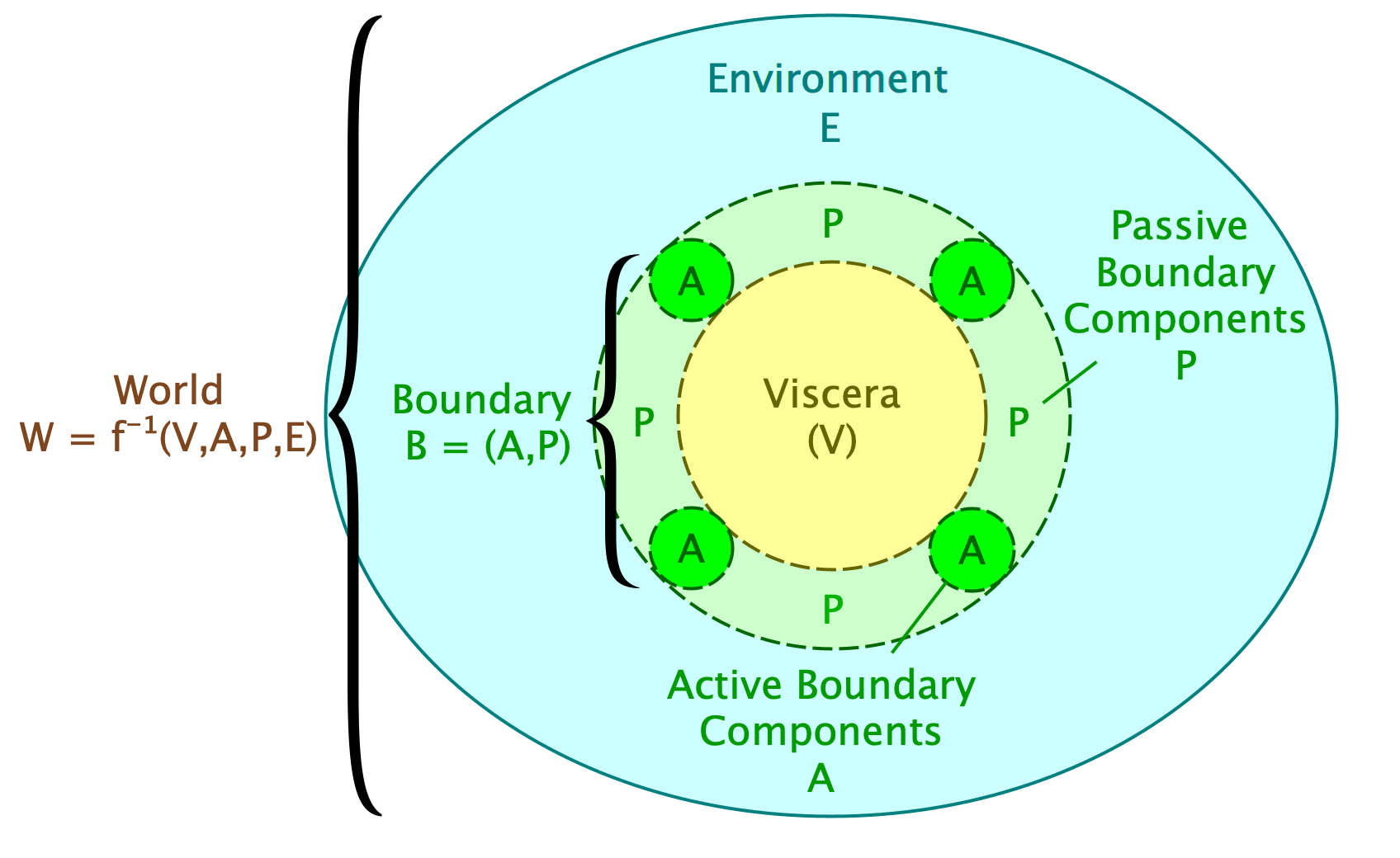
Now, for the living system to exist "within" the world, the world should be factorable into features that are and are not part of the living system. In short, the state (W) of the world should be factorable into an environment state (E), the state of the boundary of the living system (B), and the state of the interior of the living system, which I'll call its viscera (V).
Definition parts (b) & (c): the active boundary, passive boundary, and viscera
We're going to want to view the system as taking actions, so let's assume the boundary state can be further factorable into what I'll call the active boundary, A — the features or parts of the boundary primarily controlled by the viscera, interpretable as "actions" of the system— and the passive boundary, P — the features or parts of the boundary primarily controlled by the environment, interpretable as "perceptions" of the system. These could also be called "input" and "output", but for later reasons I prefer the active/passive or action/perception terminology.
To formalize this, I want a collection of state spaces and maps, like so:
- the set of world states (includes everything)
- the set of viscera states
- the set of boundary states
- the set of states of the active boundary
- the set of states of the passive boundary
- , , , , ,
,
.... which fit nicely into a diagram like this:

For each time , we define a state variable for each state space, from :
Each of these factorizations are assumed to be bijective, in the sense of accounting for everything that matters and not double-counting anything, i.e.,
- is bijective;
- is bijective;
- is bijective (which follows from the above two).
These decompositions needn't correspond to physically distinct or conspicuous regions of space, but it might be helpful to visualize the world — if it were laid out in a physical space — as being broken down into a disjoint union of parts, like this:
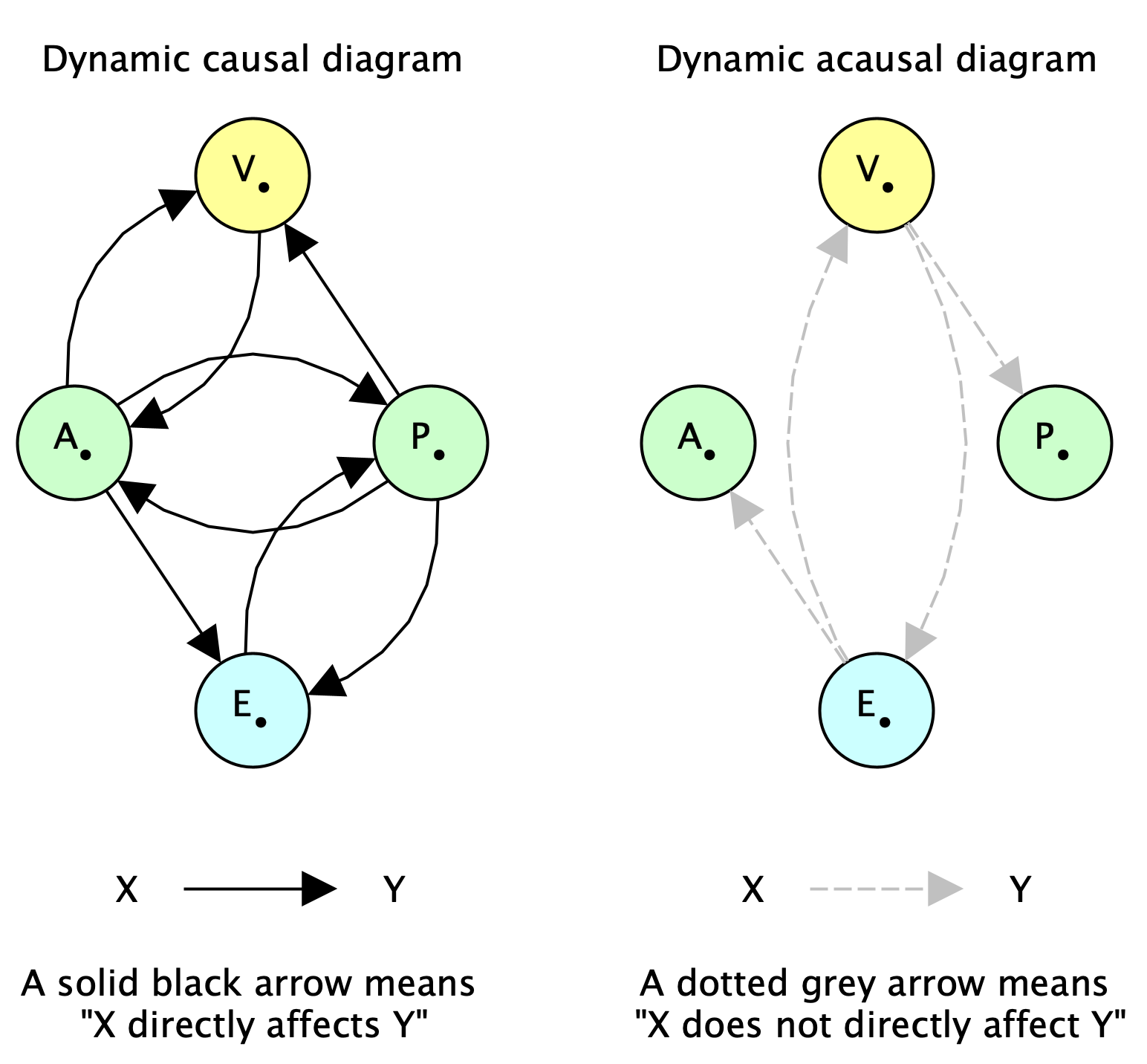
Now, when I say the boundary or its decomposition approximately causally separates the viscera from the environment, I mean that the following Pearl-style causal diagram of the world approximately holds:
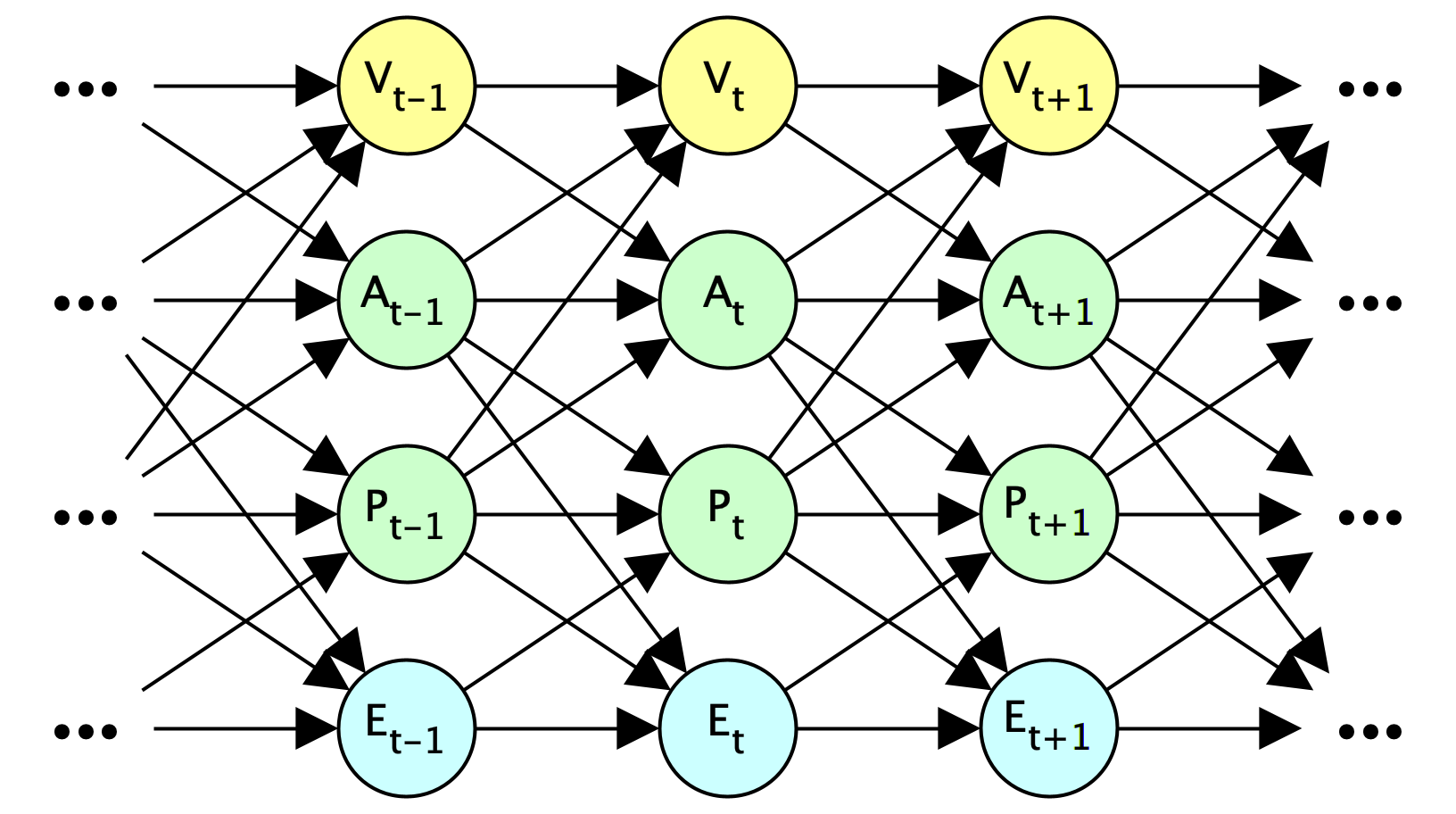
This diagram is easier to parse if we highlight the arrows that are not present from each time step to the next:

If we fold each horizontal time series into a single node, we get a much simpler-looking dynamic causal diagram (or dynamic Bayes net) and what I'll call a dynamic acausal diagram, as in the earlier Figure 1:

Since I only want to assume these causal relationships are approximately valid, let's describe the approximation quantitatively. Let denote the conditional mutual information of X and Y given Z, under any given distribution over world histories on which are defined. Let denote an aggregation function for aggregating quantities over time, like averaging, discounted averaging, or max. Define:
- "Infiltration" of information from the environment into the active boundary & viscera:
- "Exfiltration" of information from the viscera into the passive boundary & environment:
When infiltration and exfiltration are both zero, a perfect information boundary exists between in the (otherwise putative) inside and outside of the system, with a clear separation of perception and action as distinct directions of inward and outward causal influence.
With all of the above, a short yet descriptive answer to the question "what is a living system boundary?" is:
- an "approximate directed Markov blanket"
Why this phrase? Well, together the boundary (A,P) are:
- an approximate Markov blanket, meaning that A and P approximately causally separate V and E from each other, and the separation is
- "directed" in that there are discernible outward and inward channels, namely, A and P.
In the next section, infiltration and exfiltration will be related to a decision rule followed by the organism.
Definition part (d): "making decisions"
Next, let's formalize how a living system implements a decision-making process that perpetuates the defining properties of the system (including this one!). In plain terms, the system takes actions that continue its own survival. Somewhat circularly, the survival of the system as a decision-making entity involves perpetuating the particular sense in which it is a decision-making entity. So, the definition here is going to involve a fixed-point-like constraint; stay tuned 🙂
More formally, for each time step , we need to characterize the degree to which the true transition probability function
can be summarized by a description of the form "the system makes a decision about how to transform its viscera and action subject to some (soft) constraints". So, define a decision rule as any function of the form
- .
Notice how conditions on all of , while a decision rule will only look at as an input. Thus, using to predict implicates the imperfectly-accurate assumption that the system's "decisions" are not directly affected by its environment. This assumption holds precisely when the quantity is zero.
Dual to this we have what might be called a situation rule:
- .
The situation rule works well exactly when is zero. The rest of this post is focussed on , and dual statements will exist for .
As a reminder: these variables are not compressed representations. The states are not a simplified description of the world; they together describe literally everything in the world. In a later post I might talk about compressed versions of these variables that could be represented inside the mind of the organism itself or another organism, but for now we're not assuming any kind of lossy compression. Nonetheless, despite the map being lossless, probably every decision rule will be somewhat wrong as a description of reality, because by construction it ignores the direct causal influences of and on each other, of on , and of on .
Now, let's suppose we have some parametrized space of decision rules , i.e., a decision rule for every parameter in a parameter space . For example, if is defined by a neural net with a vector of weights, could be . Procedurally, could implement a process like "Compute a Bayesian-update by observing , store the result in , and choose action randomly amongst options that approximately optimize expected utility according to some utility function". More realistically, could be an implementation of a satisficing rule rather than an optimization. The particular choice of and its implementation are not crucial for this post, only the type signature of as a map .
Next, define a description error function to be a function that evaluates the error of a decision rule as a description of the true transition rule , from the perspective of anyone trying to predict or describe how the system behaves at time . For instance, we could use either of these:
- Example: , i.e., how surprising is if we predict samples from it using . Here denotes the (average) KL divergence (averaged over the value of that the two distributions are conditioned on).
Or: - Example: , where denotes an average Wasserstein distance, if there's a natural metric on , which there is for many applications.
As with the particular implementation of is not important for this post; only that it measures the failure of as a description of the system's true transition function , and in particular it should be zero precisely when agrees perfectly with . When no confusion will result, I'll write as shorthand for . Thus we have:
- Assumption: if and only if .
From this very natural assumption on the meaning of "description error", it follows that:
- Corollary: If for all , then .
In other words, for the decision rule to perfectly describe the system, there must be no infiltration, i.e., no inward boundary crossing.
Important: Note that negative description error, , is not a measure of how "optimally" the system makes decisions or predictions, it's measure of how well the rule predicts what the system will do.
Next, we need another function for aggregating description error over time, e.g., max or avg. Here may or may not be the same as the previous function, but there should be some relationship between them such that bounding one can bound the other (e.g., if they're both Avg or Max then this works). For any such function , define an aggregate description error function as
We say is a good fit for the time interval if is small. This implies several things:
- infiltration can't be too large in that time interval, i.e., the boundary remains fairly well intact;
- for each , do not destroy the present or subsequent validity of too badly, i.e., the system "makes sufficiently self-preserving choices"; and
Thus, if is a good fit, then 1 & 2 together say that the decisions made by will perpetuate the four defining properties (a)-(d) of the definition.
Dual to this, for a situation rule to work well requires that exfiltration is not too large, and for each , do not destroy the present or subsequent validity of too badly, i.e., the environment "is sufficiently hospitable". This may be viewed as a definition for a living system having a niche, a property I discussed as a subsection of Part 2 in the context of jobs and work/life balance.
Together, the survival of the organism requires both and to not violate the future validity of and too badly.
Discussion
Non-violent boundary-crossings
Real-world living systems sometimes do funky things like opening up their boundaries for each other, or even merging. For instance, consider two paramecia named Alex and Bailey. Part of Alex's decision rule involves deciding to open Alex's boundary in order to exchange DNA with Bailey. If Alex does this in a way that allows Bailey's decision rule to continue operating and decide for Bailey to open up, then the exchange of DNA has not violated Bailey's decision rule. In other words, while there is a boundary crossing event, one could say it is not a violation Bailey's boundary, because it respected (proceded in accordance with) Bailey's decision rule.
Respect for boundaries as non-arbitrary coordination norms
Epistemic status: speculation, but I think there's a theorem here.
In my current estimation, respect for boundaries as described above is more than a matter of Alex and Bailey respecting each other's "preferences" as paramecia. I hypothesize that, in the emergence of fairly arbitrary colonies of living systems, standard protocols for respecting boundaries tend to emerge as well. In other words, respect for boundaries may be a "Schelling" concept that plays a crucial role in coordinating and governing positive-sum interactions between living systems. Essentially, preferences that are easily expressed in broadly and intersubjectively meaningful concepts — like Shannon's mutual information and Pearl's causation — are more likely to be pluralistically represented and agreed upon than other more idiosyncratic preferences.
Incidentally, respect for human autonomy — the ability to make decisions — is something that many humans want to preserve through the advent of pervasive AI services and/or super-human agents. Interestingly, respect for autonomy is one of the most strongly codified ethical principles for how the scientific establishment — a kind of super-human intelligence — is supposed to treat experimental human subjects. See the Belmont Report, which is not only required reading for scientists performing human studies at many US universities, but also carries legal force in defining violations of human rights by the scientific establishment. Personally, I find it to be one of the most direct and to-the-point codifications of how a highly intelligent non-human institution (science) is supposed to treat human beings.
Comparison to related work
Cartesian frames
The formalism here is lot like a time-extended version of a Cartesian Frame (Garrabrant, 2020), except that what Scott calls an "agent" is further subdivided here into its "boundary" and its "viscera". I'm also not using the word "agent" because my focus is on living systems, which are often not very agentic, even when they can be said to have preferences in a meaningful way. After a reading of this draft, Scott also informed me that he'd like to reserve the use of the term "frame" when talking about "factoring" (in feature space), and "boundary" for when talking about "subdividing" (in physical space). I agree with drawing this distinction, but neither Scott nor I is currently excited about the word "frame" for naming the dual concept to "boundary".
Active inference
The physical ontology here is very similar to Prof. Karl Friston's view of living systems as dynamical subsystems engaging in what Friston calls active inference (Friston, 2009). Notably, Friston is one of the most widely cited scientists alive today, with over 300,000 citations on Google Scholar. Unfortunately, I find Friston's writings to be somewhat inscrutable regarding what does or doesn't constitute a "decision", "inference", or "action". So, despite the at-least-superficial philosophical alignment with Friston's perspective, I'm building things mathematically from scratch using Judea Pearl's approach of modeling causality with Bayes nets, which I find much more readily applicable in a decision-theoretic setting.
After finishing my second draft of this post, I found out about a book by two other authors trying to clarify Friston's active inference principle, with Friston as a co-author (Parr, Pezzulo, and Friston, 2022), which seems to have gained in popularity since I began writing this sequence. Unlike me, they assume the system is a "minimizer" of a free energy objective, which I think is a crucial mistake, on three counts:
- Many organisms are better described as satisficers than optimizers.
- The presumption of energy minimization fails to notice collective bargaining opportunities whereby organisms can conserve energy to spend on other (arbitrary/idiosyncratic) goals, effectively "combatting moloch" in the language of Scott Alexander (2014).
- Rather than minimizing surprise to their world models, I think real-world organisms are more likely to exist due to a tendency to perpetuate their functioning as decision-making entities.
Despite these differences, on page 44 they draw a decomposition nearly identical to my Figure 1, and refer to the separation of the interior from the exterior as a Markov blanket. They even talk about communities as having boundaries, as in Part 1 of this series: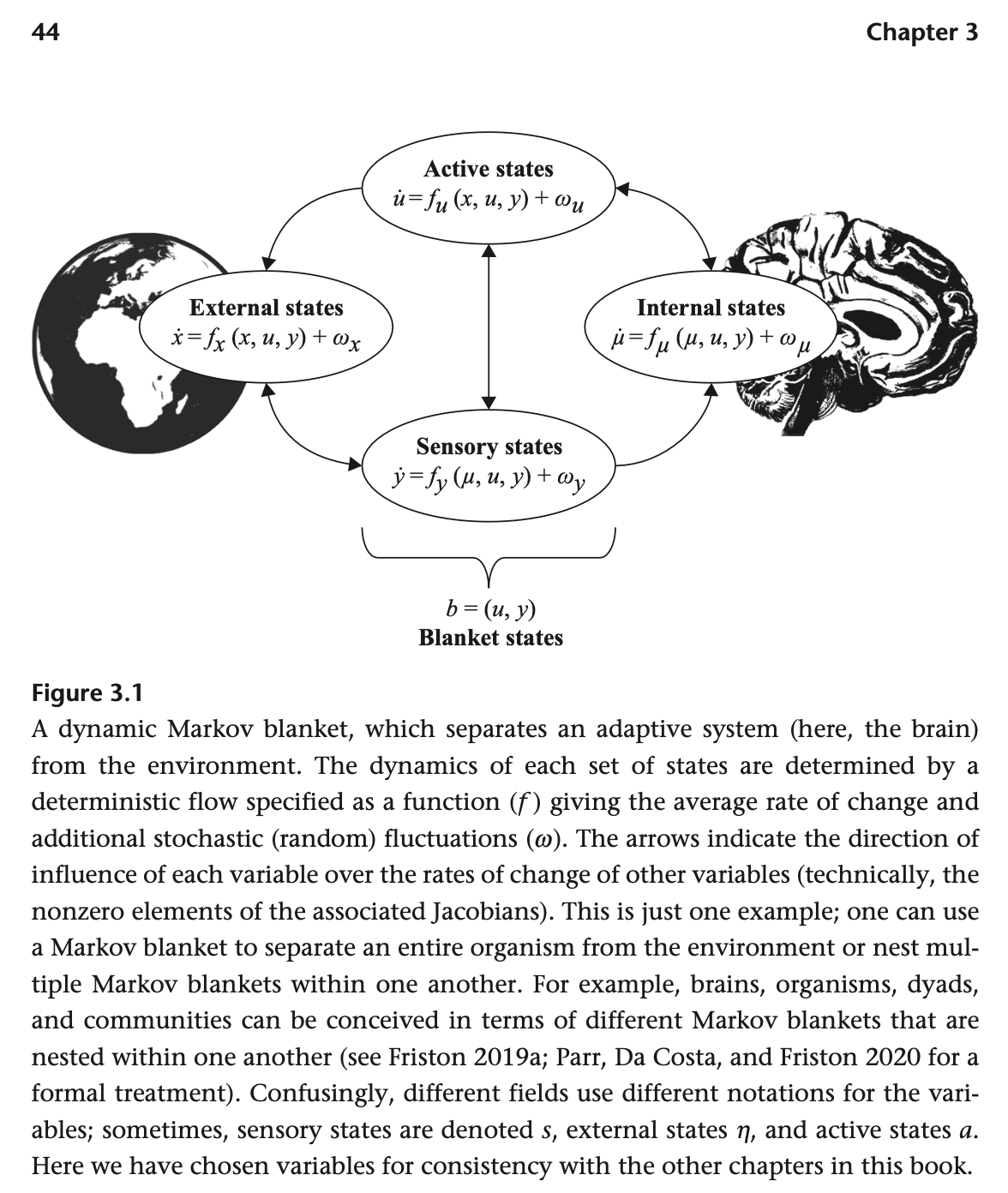
Overall, I find these similarities encouraging. After so many people being inspired by Friston's writings, it makes sense people are converging somewhat to try to clarify ideas in this space. On page ix, Friston humbly writes:
"I have a confession to make. I did not write much of this book. Or, more
precisely, I was not allowed to. This book’s agenda calls for a crisp and clear
writing style that is beyond me. Although I was allowed to slip in a few of my
favorite words, what follows is a testament to Thomas and Giovanni, their deep
understanding of the issues at hand, and, importantly, their theory of mind—in
all senses."
Functional decision theory (FDT)
FDT (Yudkowsky and Soares, 2017) presents a promising way for artificial or living systems in the physical world to coordinate better, by noticing that they're essentially implementing the same function and choosing their outputs accordingly. When an agent in the 3D world starts thinking like an FDT agent, it draws its boundary around all parts of world that are running the same function, and considers them all to be "itself". This raises a question: how do two identical or nearly identical algorithms recognize — or decide — that they are in fact implementing essentially the same function? I'm not going to go deep into that here, but my best short answer is that algorithms still need to draw some boundaries in some abstract algorithm space — e.g., in the Solomonoff prior or the speed prior — that delineate what are considered their inputs, their outputs, their internals, and their externals. So, FDT sort of punts the problem of where to draw boundaries, moving the question out of physical space and into the space of (possible) algorithms.
Markov blankets
Many other authors have elaborated on the importance of the Markov blanket concept, including LessWrong author John Wentworth, who I've seen presenting on and discussing the idea at several AI safety related meetings. I think for decision-theoretic purposes, one needs to further subdivide an organism's Markov blanket into active and passive components, for action and perception.
Recap
In this post, I delineated 8 problems that I intend to address in terms of a formal definitions of boundaries, and laid our the basic structure of the formal definition. A living system is defined in terms of a decomposition of the world (with state variable W) into an environment (state: E), active boundary (state: A), passive boundary (state: P), and viscera (state: V). The boundary state B=(A,P) forms an "approximate directed Markov blanket" separating the viscera from the environment, with A mediating outward causal influence and P mediating inward causal influence. This allows conceiving of the living system (V,A,P) as engaged in decision making according to some decision rule that approximates reality. In order to "survive" as an -following decision-making entity, the system must make decisions in a manner that does not bring an end to as an approximately-valid description of its behavior, and in particular, does not destroy the approximate Markov property of the boundary , and does not destroy the outward and inward causal influence directions of the passive boundary and active boundary . In other words, is assumed to perpetuate . This assumption is justified by the observation that self-perpetuating systems are made more noticeable and impactful by their continued existence.
From there, I argue briefly that non-violence and respect for boundaries are non-arbitrary coordination norms, because of the ability to define boundaries entirely information-theoretically, without reference to other more idiosyncratic aspects of individual preferences. Comparisons are drawn to Cartesian frames (which are not time-extended), functional decision theory (which conceives of decision-theoretic causation in a logical space rather than a physical space), and Friston's notion of active inference. After writing the definitions, a strong similarity was found to Chapter 3 of Parr (2022), in describing perception ("sensing") and action systems as constituting a Markov blanket, around both individual organisms and communities. However, Friston and Parr both characterize the living system in question as an optimizer, which specifically minimizes surprise to its world model. I consider both of these assumptions to be problematic, enough so that I don't believe the active inference concept is quite right for capturing respect for boundaries as a moral precept.
Reminder to vote
If you have a minute to cast a vote on which alignment-related problem I should most focus on applying these definitions to in Part 3b, please do so here. Thanks!