This post aims to quickly break down and explain the dominant mental models interpretability researchers currently use when thinking about how transformers work.
In my view, the focus of transformer interpretability research is teleological: we care about the functions each component in the transformer performs and how those functions interact to yield the capabilities we see in language models today. From a functional understanding of transformer internals, we then hope to be able to answer other important interpretability questions such as, “Where/How is knowledge stored?,” “Do transformers have beliefs?”, and “How do transformers reason?” As such, the mental models described in this post will be functional theories about how researchers think about transformer internals, and not hypotheses about other interpretability questions, like the ones mentioned above.
There are three main components at work in the transformer: the attention heads, the MLP, and the additive residual stream that connects all the layers. The functions that each play aren’t clear and are the subject of much research, and the mental models described below will be different ways of thinking about each main component. None of these mental models are mutually exclusive, and in reality, transformer internals probably look like a messy combination of many of these models.
This post assumes a working understanding of transformers. For a primer on the transformer architecture, I recommend The Illustrated Transformer, Transformers from Scratch, and The Annotated Transformer. Other works that this post draws greatly from are the logit lens, Transformer Feed-Forward Layers Are Key-Value Memories, ROME, and the Anthropic papers.
The Models
Residual Stream as Output Accumulation
The residual stream is simply the accumulation of all the stuff the transformer wants to say at the end of its inference step.
Clearly, the last residual hidden state is the transformer’s prediction (before it gets projected to the vocabulary), and all this mental model is suggesting is that the prior hidden states are less-refined versions of the final residual hidden state. The strongest version of this model states that the middle hidden states are the model’s nascent predictions, and the weaker version just states that the middle hidden states contain the model’s nascent predictions. This model seems pretty intuitive, and its weaker version seems pretty true to me.
The strongest source of evidence for this model currently is the logit lens. In a really neat trick, which they dubbed the logit lens, nostalgebraist found that by projecting the intermediate hidden states of GPT2 to the vocabulary matrix, the resulting logit distributions made a lot of sense. The logit lens might be a way to see what GPT believes at each time step in its processing, and with it, we can see some surprisingly coherent and logical “thought processes.”
How to read this table: The token at the bottom of each column is the last token in the input sequence; the token at the top of each column is the correct token; the tokens in-between are the projections of GPT2’s hidden states to the vocab.
When GPT2 is faced with an easy prediction task, such as induction (“Mr. Dursley”) or stop words (“director of”) — words that have super high bigram log likelihoods — the logit lens shows that it converges to that prediction rapidly, and when it’s faced with a harder task, we see that difficulty reflected accordingly in the flatness of its logit distribution. Additionally, GPT2’s intermediate projections make sense. If we just read the projections for the column with the input token as “the,” we read “same, first, only, youngest, only” which sounds like GPT2 thinks that the sentence is going to describe Mr. Dursley as an only child, youngest child, first-born, etc.
One common perspective in deep learning is the information bottleneck perspective, which states that deep learning models try to transform their input representations to encode as much information about the output as possible, while removing irrelevant information about the input. In the logit lens table above, we can see that by the first layer, the residual hidden state usually does not project out to the original input token. What this suggests is that GPT, and autoregressive transformers in general, immediately converts inputs to guesses about the output, working in an output-prediction space more than an input-compression space.
The strong version of this mental model, which specifically states that the residual hidden states are distributions over the output vocabulary, is also kind of intuitive. Weak evidence for the strong version of this mental model, that the intermediate hidden states are the model’s final prediction, is this quick PCA experiment I ran. If you run PCA on all of a model’s residual states for a given prediction, there’s a single direction that explains roughly 88% of the variance across all layers. And if you project this direction to the vocab, it’s usually (~77% of the time) the model’s final prediction.
Residual Stream as Communication Channel
Another way of thinking about the residual stream is that it’s a communication channel for individual components of the transformer to talk through. This perspective was introduced in Anthropic’s first paper about mechanistic interpretability and seems to be the group’s take on the residual stream in general. Importantly, thinking about the residual stream as a communication channel or as an accumulation of output is not mutually exclusive, and, in fact, the accumulation of information about the output, seen in the logit lens, is probably being communicated to components deeper in the transformer.
The nature of the residual stream is that it’s a linear, vector space that is being added to and read from by all layers. The attention heads and MLP will read from the space with a linear projection — with the query and key matrices and the first linear transformation in the MLP respectively — and then write to the residual by adding another linear transformation — the value and output matrices and second linear transformation in the MLP respectively — back into the residual. And since the residual doesn’t do any processing itself, it’s intuitive to think of it as the space where all the attention heads and MLP neurons communicate through.
There are a couple of components that have been found in transformers that seem to be doing communication-like things. The most notable component is, of course, induction heads. Induction heads are pairs of attention heads that seem to implement an induction-like algorithm, specifically an algorithm that completes the pattern AB … A -> B. They work by searching through the context, finding the present token, and then attending to the token that comes after the present token. Since these induction heads involve pairs of heads across layers, they communicate through the residual stream, where the first induction head copies information with its OV matrix about the present token, which the key matrix of the second induction head reads.
Anthropic also found evidence of neurons in the MLP and attention heads that seem to delete information from the residual stream. Specifically, the MLP neurons have input weights that have very high negative cosine similarity with their output weights, indicating that if a direction is present in the residual stream, the neuron will add in the negative of that direction into the residual stream. The attention heads had highly negative eigenvalues in their OV matrix and seemed to attend to the present token, indicating that they delete information about the present token.
MLP as Key-Value Pairs
The Feed-Forward (FF) in a transformer is defined as 2 linear transformations of the input with a non-linearity (ReLU, GeLU, etc.) in between, i.e:
In the paper, Transformer Feed-Forward Layers Are Key-Value Memories, Geva et al. propose a mental model for thinking about the MLP where the first linear transformation are keys and the second linear transformation are values. Together, they form key-value pairs or neural memories, which can be written as (omitting the biases):
where is some non-linearity
Since each key-value pair corresponds to columns in the MLP weights, we can rewrite the above as:
where is the coefficient of and is the MLP’s hidden dimension (typically 4 times the model embedding size)
The key-value pair mental model states that when a key is activated by "something", its corresponding value will be written strongly into the residual (since the coefficient will be high). This alone is pretty straightforward and seems right; the important thing is what you interpret this "something" as.
This "something" according to the key-value paper are patterns: each key is activated by textual patterns in its training data, and when a key is activated, its corresponding value will shift the residual’s logit distribution (with the mental model of the residual stream as output accumulation) towards a distribution that complements the logits that would typically appear after the textual pattern correlated with the key. This correlation between key and value is particularly noticeable in higher layers i.e. the key-value pairs in higher layers are more likely to contain semantic information, while lower layers contain shallow (syntactic or grammatical) information.
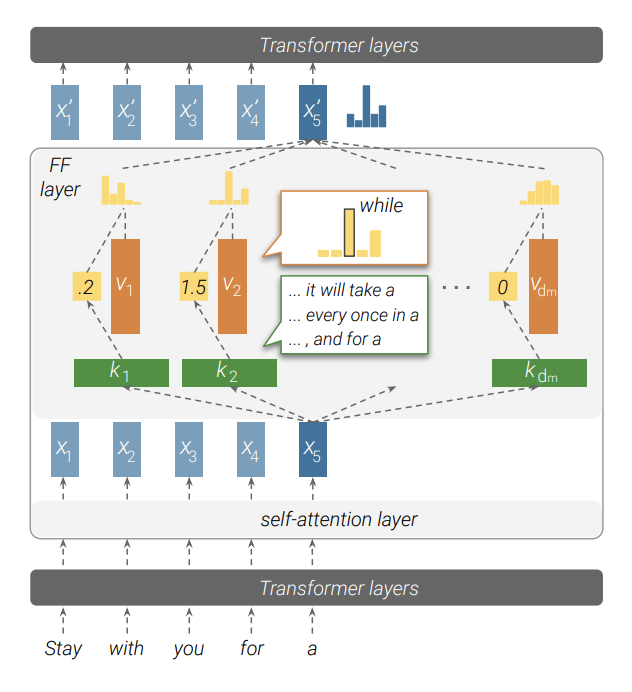
The key-value mental model suggests that the MLP is where knowledge is stored (since you can treat key-value pairs as a linear-associative memory). For example, maybe values contain knowledge and write that knowledge into the residual stream. Multiple knowledge editing methods have made use of this implication. In Rank-One-Model-Editing (ROME), they used the key-value model for their knowledge editing procedure, and the fact that ROME works really well supports the key-value model’s validity.
Attention as Information Movers
I think this mental model is the least controversial of all the ones mentioned in this post. The very structure of attention suggests that its function is centered around the context and the different relationships between tokens in a sequence. How else would information move across tokens?
Besides the intuitive-ness of this mental model, there’s a lot of empirical evidence that backs it up. Obviously, the existence of induction heads supports the mental model that attention heads move information across tokens. Additionally, in the ROME paper, their causal tracing method supports the idea that attention heads move information across tokens. Specifically, their causal tracing suggests that attention heads move factual knowledge about tokens that the MLP writes into the residual stream towards the prediction of the final token in the sequence. I’d just direct readers to the actual paper if they want to learn more about this stuff because it’s pretty cool.