From a zoomed-out perspective, the model is not modifying the loss landscape. This frame, however, does not give us a useful way of thinking about how gradient hacking might occur and how to avoid it.
I think that the main value of the frame is to separate out the different potential ways gradient hacking can occur. I've noticed that in discussions without this distinction, it's very easy to equivocate between the types, which leads to frustrating conversations where people fundamentally disagree without realizing (i.e someone might be talking about some mins of the base objective being dangerous, while the other person is talking about the model actually breaking SGD and avoiding mins entirely). Illusion of transparency and all that.
For instance, when you mention that "[continuously failing] gradient hacking will in general lead to worse performance on the base-objective" -- this is only true for nonconvergent gradient hackers! I can see where you're coming from; most mesaobjectives have mins that don't really line up with the base objective, and so a lot of the time moving towards a min of the mesaobjective hurts performance on the base objective. In some sense, convergent gradient hackers are those whose mins happen to line up with the mins of the base objective. However, even though in some intuitive sense convergent mesaobjectives are very very sparse in the space of all mesaobjectives, it's very likely that convergent mesaobjectives are the ones we think are actually likely to exist in the real world (also, as a data point, Evan says that convergent gradient hackers are what he considers "gradient hacking" for instance).
In fact, I'd argue that coupling, assuming it were possible for the sake of argument, would imply a convergent gradient hacker (the reverse implication is not necessarily true) -- a rough and not very rigorous sketch of the argument: if the model remains coupled across training, then at any point in training any epsilon change which hurts the mesaobjective must also hurt the base objective, thus the inner product of the mesa gradient and base gradient must always be nonnegative, thus if SGD converges it must converge to a min or saddle point of the mesaobjective too (whereas the hallmark of nonconvergent gradient hackers is they manage to find a min of the mesaobjective somewhere where base gradient is nonzero).
I think this is a totally fine length. But then, I would :P
I still feel like this was a little gears-light. Do the proposed examples of gradient hacking really work if you make a toy neural network with them? (Or does gradient descent find a way around the apparent local minimum?)
This post was written under Evan Hubinger’s direct guidance and mentorship, as a part of the Stanford Existential Risks Institute ML Alignment Theory Scholars (MATS) program.
Additional thanks to Michele Campolo, Oliver Zhang, Adam Shimi, and Leo Gao for their thoughts and feedback on this post. This work is additionally supported by CEEALAR.
TL;DR: Gradient hacking describes how a deceptively misaligned mesa-optimizer could influence its own training process via its outputs and thinking process. This is mainly considered in the context of training a neural network with gradient descent. A deceptive mesa-optimizer would have strong incentives to gradient hack; to protect its mesa-objective from being overwritten by the training process, to prevent humans from discovering the deception, and to build its own misaligned capabilities. I think gradient hacking is only plausible if the model’s ability to gradient hack is strongly coupled to the model’s general capability to perform well on tasks, such that attempting to remove the gradient hacking ability causes a large drop in the model’s performance. If there is not this strong coupling I expect the gradient hacker to not be stable, and to be erased by gradient descent.
When attempting to prevent gradient hacking, we do not want to be in the position where we are attempting to look for a model performing gradient hacking; if a model is able to gradient hack then it may be able to competently hide itself from us. Rather we should attempt to design our training procedures such that gradient hacking never happens.
What is gradient hacking?
Gradient hacking is a potential phenomenon where a machine learning model is able to influence its training process via its outputs and push its parameters in directions it desires. When a model is being trained by a local-optimization procedure such as gradient descent, it can deliberately choose certain outputs or ways of thinking to ensure the gradients are what it wants, and hence the parameter updates are in line with its own objectives. Here it is choosing its outputs and thought process to ‘hack’ the gradients and influence its training. This is most worrying if we have a deceptively aligned model, which is attempting to pretend to be aligned while actually having its own goals which are not aligned with ours. Such a gradient hacking model may choose its outputs in such a way that optimizes its mesa-objective rather than doing what we actually want. So far gradient hacking is still theoretical and seems to require a relatively powerful mesa-optimizer. But if a powerful mesa-optimizer does develop in a prosaic AI model, then it seems likely that it would attempt to gradient hack.
A gradient hacker may choose to protect parts of itself from various aspects of the training process which would cause it to be erased, or it may seek to deliberately modify its weights to better achieve its mesa-objective. For example, if we were using transparency tools to deliberately look for deceptive alignment in our model, then a gradient hacker could change its weights to trick us or better conceal itself. For this reason, if gradient hacking is plausible then it is essential that our training process never produces one in the first place. We cannot be in the position of ‘putting out fires’ here; once a model has started to gradient hack it may already be too late because our transparency tools and other attempts to discover misalignment may be rendered useless.
Gradient hacking has a seemingly recursive nature; the model has to reason about its training process to choose how to affect the gradients of its parameters, but this very reasoning process influences the gradients. The model is made up of parameters, and these parameters are trying to influence themselves. This feels a bit like trying to do brain surgery on yourself and whenever you think about moving the scalpel this very thought changes your brain slightly.
Loss landscapes and determinism
Gradient hacking can be conceptually difficult to think about, and I think that explicitly thinking about gradient descent traversing the loss landscape is not a particularly helpful framing. See this post for a thorough discussion of gradient hacking and loss landscapes.
In the case of a stationary loss landscape, when a model gradient hacks all that is happening is standard gradient descent. The model parameters are simply being updated according to gradient descent (and not any other tricks). From a zoomed-out perspective, the model is not modifying the loss landscape. This frame, however, does not give us a useful way of thinking about how gradient hacking might occur and how to avoid it. As an analogy, we can consider the world with humans making choices and taking actions. It is perfectly correct to think of this world just in terms of atoms moving around according to the laws of physics (like the model parameters changing according to the rules of gradient descent), but this view would not offer us a useful way of thinking about the actions humans take. From the point of view of the gradient hacker, it is capable of making choices and taking actions, even though on one level this is just gradient descent.
For gradient hackers, we can think about a model with parameters Θ, which can make choices and also has partial control over models close to it in parameter space (in a similar way to how a human can make choices and in some sense has partial control over actions they take in the future). The closer in parameter space ΘT is to ΘT+1, the more control the model with parameters ΘT has over the model with parameters ΘT+1.
There are cases where the loss landscape is non-stationary, and the model has the opportunity to influence its own training data. For example, in reinforcement learning where the model can affect which experiences it has and hence its training data. In this case, a gradient hacker can have the type of control as described above, and it may be able to sculpt the loss landscape so that gradient descent modifies its parameters in desirable ways. This seems analogous to a human being able to make choices for themselves, and also put themselves in environments where they know they are likely to make good choices.
Why might it happen?
A mesa-optimizer is likely to have reasons to want to influence its training process. If there is deceptive misalignment between the mesa-objective and the base-objective, it will be very unlikely that continuing to straightforwardly optimize for the base-objective will lead to good performance on the mesa-objective. There are two (rather obvious) categories of reasons a mesa-optimizer would want to gradient hack: to prevent things it doesn’t want and to cause things it does want. Here are some examples of reasons for a model to gradient hack, but this is in no way exhaustive.
Gradient hacking to prevent things
Being removed by the training process
Perhaps the most simple incentive for a mesa-optimizer to gradient hack is to stop itself from being removed by the training process. If the mesa-optimizer is erased by the training process then it obviously won’t be able to continue pursuing its mesa-objective. The region of the parameter space that actually implements a specific mesa-optimizer will be very small (compared with the whole space), and so any change to the parameters that isn’t selected to improve or not modify the mesa-optimizer is likely to hurt it. This could be either by erasing or modifying the mesa-objective or making the mesa-optimizer perform less well on this mesa-objective. So the mesa-optimizer has an incentive to protect itself from most changes which could be made to the network.
There seem to be two importantly different regimes here, where the mesa-optimizer could use gradient hacking to fight against different things.
In the nonzero-loss regime, there is pressure from gradient descent to improve performance on the base-objective. Because the mesa-objective is not the same as the base-objective, naively changing the weights to improve the performance on the base-objective is likely to hurt performance on the mesa-objective. For example, because pushing the weights to perform better on the base-objective will push them away from where they lead to good performance on the mesa-objective. If these weights are changed enough this would entirely just erase the parameters which instantiate the mesa-optimizer, or at least modify the mesa-optimizer such that it is no longer optimizing for the same mesa-objective.
In the zero-loss regime, optimization for the base-objective is no longer applying a strong pressure on the weights, and instead, the main pressure will be due to the inductive biases of the training process. For neural networks trained with SGD, these inductive biases push towards simplicity, and again any changes to the network (including being made more simple) are likely to modify it in ways which decrease performance on the mesa-objective.
From “Risks from Learned Optimization”, one of the reasons to expect mesa-optimization in the first place was because of this push towards simplicity; a learned optimizer is likely a simple model that is able to perform well at a complex task. But the first mesa-optimizer encountered in training is unlikely to be the most simple, and so a mesa-optimizer will still have to fight this pressure towards simplicity to avoid being pushed to become an even simpler (but different) mesa-optimizer.
Additionally in both of these regimes, there may be regularization which the mesa-objective has an incentive to counteract. A clear example here is weight decay regularization, where there is pressure to decrease the values of the parameters. If left unchecked, this will erase or modify the mesa-optimizer and so again there is an incentive to gradient hacking to stop this happening.
For gradient descent using weight decay regularization we have Θi←Θi−ΔΘi, where ΔΘi=α∗(∂∂ΘiL+ΛΘi). Here the effect of weight decay regularization could be cancelled out by having the loss depend quadratically on each parameter
L=−Λ/2∑iΘ2i+B
This likely seems difficult to achieve but there may be approximations which can reduce the effects of weight decay. At least in this very simple model the gradients can be set up to resist the effects of weight decay.
Being discovered
A deceptively aligned model has incentives to keep its deception hidden, because if discovered the model may be turned off or modified to remove the deception. Therefore gradient hacking may be used to actively make the deception harder to notice. This applies both for humans using transparency tools to manually check the model, and for more automated approaches such as using an automated benchmark or other metric to evaluate the probability of deception. Deception is likely to be already reinforced by gradient descent, because becoming more deceptive means the model will perform better on the base-objective rather than pursuing its mesa-objective. This style of deception may just result in the model modifying its outputs to agree with the base-objective, and not attempt to disguise its deception as it may by using gradient hacking.
As one example, humans may use transparency tools to check that a model isn’t performing optimization (as this may lead to dangerous mesa-optimization). A deceptive model may evade these tools, and still optimize for its mesa-objective by using gradient hacking to hardcode actions which will perform well on the mesa-objective while simultaneously removing the part of itself which actually performs optimization. In this situation, we see how the mesa-optimizer’s preference for self-preservation is just instrumental for achieving its mesa-objective. If it decides that erasing itself will lead to better performance on its objective, then the mesa-optimizer will do this.
There is a similar scenario if the humans are aiming to only create myopic models, which don’t have any objectives which extend across parameter updates. A model may start non-myopic, then gradient hack itself to perform specific actions in the future and also to make itself become myopic. This model would not be discovered by non-myopia detection tools, but would also perform actions according to a non-myopic objective. Therefore to be confident that a model will not perform non-myopic actions we have to be confident that it has been myopic from the start.
Gradient hacking to cause things
Improve the mesa-optimizer
A mesa-optimizer obviously has strong incentives to improve its ability to fulfil its mesa-objective. It will be incentivized to improve its capabilities without changing what is actually being optimized for. This may be easier or harder, depending on how coupled the model’s optimizing ability is to its objective. For example, if a mesa-optimizer has learned a very specific algorithm to optimize for a specific thing then it could be hard for the mesa-optimizer to modify itself to increase its capabilities without changing what is being optimized for. However, it seems more likely the model’s capabilities will be reasonably decoupled from the specifics of the mesa-objective because I expect the mesa-optimizing model to develop out of an already very competent model (as we will see in the section on Plausibility).
In the situation where improving the model’s performance on the mesa-objective leads to improved performance on the base-objective, if a model is gradient hacking to improve itself this may look like the emergence of spontaneous meta-learning (LINK). Here the model may be influencing its training to make itself more generally capable. For example, the implicit biases of the training process may prevent it becoming optimally capable, and so the mesa-optimizer may ‘take over’ the training process to improve its capabilities; or the mesa-optimizer may just want to become capable as quickly as possible. This would be a useful instrumental goal for the mesa-optimizer and could give the impression that the model was training exceptionally well on the base-objective. This may be something to look for when checking for mesa-optimization and gradient hackers specifically; if the training process seems to improve for unknown reasons this could be a sign that the model is influencing its own training process. But it is also unclear if this would look significantly different from normal gradient descent just finding a better way of solving a problem. Additionally, a sufficiently capable and deceptive model may realize we are looking for this and so attempt to improve its capability on the mesa-objective without improving general capabilities.
A gradient hacking model could attempt to improve itself by modifying which algorithms it is running. It may have a solid mesa-objective and a moderately capable optimization algorithm, and use gradient hacking to improve this algorithm. It may seem difficult for the model to change algorithms continuously such that it doesn’t just break. There needs to be a continuous path through the parameter space from Algorithm 0 to Algorithm 1. But this is exactly what gradient descent does when neural networks learn to be more capable.
If a mesa-optimizer begins as a subnetwork it could use gradient hacking to ‘take over’ the rest of the network. There could be a mesa-optimizing subnetwork, which does all of the useful computation leading to good performance on both the base-objective and the mesa-objective. It may be useful for such a mesa-optimizer to start using the rest of the network for its own computation. This seems analogous to the model gaining more computational power; the mesa-optimizer would be able to be more capable if it was using the entire network rather than just a subnetwork. In general larger networks have the capacity to be more capable than smaller networks.
Remove self-oversight capabilities
Many of the proposals for building safe AI have a model involved in performing oversight checks on a version of itself. For example, using a combination of a human and a model M to inspect a copy of M for deception or other bad behavior. As models become larger it seems as if unassisted humans will be less and less able to perform these oversight checks and so will rely more on the model itself. A model which is found to be deceptive is likely to either be immediately turned off or modified to remove the deception. Therefore a mesa-optimizer has a very strong incentive to remove its ability to perform these oversight checks.
A deceptive model in this situation may also gradient hack to better deceive a human overseer. It could do this by improving its ability to lie to humans about the existence of mesa-optimization and deception. This behavior also seems like it may be reinforced by regular gradient descent; a model which successfully convinces a human there is no deception will receive a low oversight loss regardless of whether or not it is lying.
As noted above, this means that for oversight and transparency tools to work for building safe AI we need to ensure that these models are not deceptive from the very beginning of training. These tools also can’t be ‘leaky’ and allow for the model to ever become deceptive, even for one timestep. If a model becomes deceptive then it can begin to lie to the human, and humans can no longer trust the model for oversight. This would allow the model to start improving its misaligned capabilities, while keeping any human overseers blind to any deception or misalignment.
Remove parts of the network which hurt mesa-objective performance
If a network is not fully unified in its goals, or sometimes takes actions which work against the mesa-objective, then a mesa-optimizer has incentives to remove these parts of the network which are not aligned with its goals. For example, we could have an RL agent which develops a strategy early in training, and if a mesa-optimizer later arises this learned strategy could lead to bad performance on the mesa-objective. The mesa-optimizer, therefore, has a strong reason to gradient hack and remove the parts of the model which lead to these ‘bad’ actions.
In a more unlikely case, we could have two separate mesa-optimizers develop as different subnetworks in the same overall model. These two mesa-optimizers would almost certainly have different mesa-objectives and so would have strong incentives to attempt to remove the other. Even if these two subnetworks are able to coordinate and not destroy each other, they would still not be aligned with the human objectives, which from our human perspective is just as bad.
Plausibility
There seem to be some plausible and strong incentives for a mesa-optimizer to gradient hack and influence its training process. But it is still uncertain whether this is actually plausible in practice. Specifically, could we have models which have some influence over their training process and are not just overwritten by gradient descent, and could such models arise in practice?
Coupling
I think that gradient hacking models can both plausibly exist, and can be plausibly found by gradient descent. But this depends almost entirely on how ‘coupled’ the model’s ability to do gradient hacking is with the general capabilities of the model. By general capabilities I mean the model’s ability to act competently. I expect that if a mesa-optimizer is able to perform well on both the base-objective and the mesa-objective then this good performance comes from some underlying general capability. This general capability can be thought of in terms of the model’s optimization power; a more capable model has greater optimization power, without having to specify which objective this optimization power is directed at.
Here I’ll use the terms ‘coupled’ and ‘coupling’ to refer to how linked a model’s general capabilities are to its ability to gradient hack. If these are strongly coupled then breaking the gradient hacking capabilities will cause a large decrease in the general capabilities of the model. This would mean that gradient descent would have difficulty removing the gradient hacking capabilities, because locally any step which decreased the ability to gradient hack would also decrease the model’s general capabilities, leading to worse performance on the base-objective. Because gradient descent is a local optimization procedure, it doesn’t take steps that locally lead to worse performance on the base-objective.
If there is not strong coupling between the model capabilities and its gradient hacking capabilities, then it is possible to break the model’s ability to gradient hack without breaking its ability to perform well on other tasks. The model’s optimization power wouldn’t decrease if we removed its ability to gradient hack. Such a situation could arise if there was a subnetwork performing gradient hacking, and a separate subnetwork doing the ‘useful’ computation. Here removing the gradient hacking subnetwork would have minimal effect on the model’s ability to do well on the base-objective.
As another neurosurgery metaphor, when thinking about strong and weak coupling we can consider the difference between a mental disorder caused by the fundamental structure of the brain versus a disorder with similar effects caused by a brain tumor. If a disorder is caused by the fundamental structure of the brain, then no amount of brain surgery will be able to correct it without incapacitating the patient. Here we could say that there is strong coupling between the mental disorder and the patient’s general capabilities. While if the disorder is caused by a brain tumor pressing on other parts of the brain, then the disorder may be able to be cured without incapacitating the patient by removing the tumor. Here the mental disorder is not strongly coupled to the patient’s general capabilities, because we are able to cure the disorder without disrupting the general capabilities.
Can gradient hacking models arise?
Before considering whether it is possible for gradient hackers to exist and remain stable, we should first consider whether they can arise in the first place as a result of gradient descent. I think the possibility of gradient hackers first appearing is likely to depend on how coupled are the gradient hacking capabilities and the general capabilities of the model.
In the post “Thoughts on Gradient Hacking”, Richard Ngo brings up a point about the difficulty of actually beginning to gradient hack for the first time. The first time a model starts to gradient hack, its weights will be close to a region where the model wasn’t previously gradient hacking. So if this gradient hacking causes the model to perform worse on the base-objective, then gradient descent will push the weights of the model back into a region where it no longer gradient hacks. In this situation the gradient hacker is optimizing for the mesa-objective, hence leading to less good performance on the base-objective.
One plausible way a gradient hacker could get started is if it starts from an already capable model. Gradient descent may find a mesa-optimizing model, which is generally capable due to the fact that it is an optimizer. This model develops general capabilities, which give it the ability to perform gradient hacking before it actually attempts gradient hacking for the first time; the model is capable of gradient hacking but just hasn’t ‘decided to’ yet. Because the model’s ability to gradient hack comes from its optimization power which gives it its general capabilities (i.e. strong coupling), when it first decides to gradient hack, gradient descent will not be able to remove this ability without hurting performance. When the model first started gradient hacking, its weights were already solidly in a region where it was capable of gradient hacking and so it can’t easily be pushed into a non-gradient hacking region.
It seems quite unlikely that gradient descent would stumble into a gradient hacking model without first being a generally capable mesa-optimizer, because gradient hacking seems likely to require quite advanced capabilities (such as some knowledge of the base-objective and training process). Even if gradient descent did stumble into a gradient hacking model without being generally capable, the weights would likely be pushed back into a non-gradient hacking region due to poor performance on the base-objective. And even if the gradient hacker managed to be stable initially, without coupling between the gradient hacking and general capabilities, over time the pressures and drifts due to gradient descent would likely erase the gradient hacker.
As brought up in ‘Thoughts on Gradient Hacking’, this difficulty getting started and remaining stable could also be ‘solved’ in a situation where the model is able to influence the loss landscape. For example, this could be in an RL context or a language model where the model outputs fed back in as inputs. Here the agent could ‘leave messages’ to its future self to make it more likely to continue gradient hacking, or otherwise shape the loss landscape such that gradient descent doesn’t push the weights out of the region where it gradient hacks.
Can gradient hacking models be sustained?
As stated above, I think the plausibility of models which influence their own training process depends almost entirely on the coupling between the ability to gradient hack and the models’ general capabilities. If there is strong coupling then gradient descent will not be able to overwrite the ability to gradient hack. If there is weak coupling I expect the various optimization pressures of gradient descent to mean that a gradient hacker is not stable, and will likely be erased.
In the strongly coupled regime, the model’s ability to gradient hack would arise from the same underlying capability to accomplish other things. There wouldn’t be any single part of the model that does gradient hacking, but rather the model is just generally capable and part of being generally capable is the ability to gradient hack.
We could think of ‘tying’ a separate gradient hacking module to the model’s general computation, such that if we try to remove or modify the gradient hacker it causes the general computation to break. An example of this could be rather than ever using the number 2 in the general computation, the model uses the sum of the gradient hacking weights divided by n, where n is a hardcoded constant equal to half of the sum of the weights. So here if the gradient hacking weights change, the computation can’t use the number 2 properly and so would begin to fail. This should initially keep the gradient hacking weights stable, because changing them would hurt the model’s performance. But I think over time, gradient descent would likely modify the tie between the gradient hacking weights and the general computation, replacing ∑wGH/n with just 2. This seems likely because of gradient descent’s push towards simplicity. Once the general computation is no longer tied to the gradient hacking module, gradient descent would then be able to modify the module without hurting performance on the base-objective. So although tying a separate gradient hacking module to the model’s general capability in this way can make it stable for longer, it doesn’t give the same robust stability that comes from having the gradient hacking ability and the general capability stemming from the same underlying optimization power.
This requirement for the gradient hacking capabilities to be strongly coupled to the general capabilities means that it is very difficult to design simple toy models which do some form of gradient hacking. To have this strong coupling we would need to develop some general capabilities from which the model gets its ability to both gradient hack and to perform well on the base-objective. This so far has been reasonably out of scope for the simple toy models we would want to make to test the plausibility and properties of gradient hacking.
This also makes me think that methods for gradient hacking which involve having a distinct deceptive subnetwork that is separate from the useful computation are not very plausible. It doesn’t seem like such a subnetwork would be able to influence the training process without being eventually erased by gradient descent.
How might gradient hacking be implemented?
There seem to be two main ways to classify how a model might influence its training process, depending on its level of capability. A model may attempt to directly control its gradients in order to actively shape the training process, or it may attempt to protect itself by making the training process not affect certain weights. Somewhat tautologically, a higher level of control over the training process requires a more capable model. These approaches are discussed in the post “Approaches to Gradient Hacking”, where ‘exact gradient control’ and ‘approximate gradient control’ are discussed as ways to have direct control over the gradients, while ‘gradient protection’ and ‘gradient hitchhiking’ refer to methods for protecting certain parts of a network from the training process. See that post for a thorough discussion of these different approaches.
There is also a third method, where the model is explicitly given some control over the training process, for example being able to choose the learning rate or the parts of the loss function. This may be used for gradient control or protection, but seems importantly different because the model is designed to influence its training process rather than doing this in a way that humans did not intend.
Gradient Control
For gradient control schemes, a gradient hacking model aims to modify its weights by using its influence over its outputs and thinking process. These approaches require the model to be quite capable because it needs to know (or at least work out) which modifications of its weights lead to better performance on the mesa-objective. For these methods to work, a mesa-optimizing model has to be generally competent on the base-objective; this allows the agent to choose to do well or poorly on the base-objective, effectively giving it the ability to choose its own loss.
The most advanced version of this is where the model is able to compute ‘think’ in such a way that it calculates what it wants the gradients to be, and that this same thinking process leads to the real gradients being what the model calculated. As usual, this seems recursive, where the computation of the gradients influences what the gradients should be. We can express this in a somewhat convoluted way as
∂∂ΘL(f(g(Θ),Θ))≈g(Θ)
Where Theta refers to all the model parameters, L is the loss function, f is the model, and g is the part of the model which computes what the gradients need to be to give good performance on the mesa-objective. The model f depends on g because this is part of its computation, but also separately on the model parameters as well.
Although maybe mathematically possible, this method of exact gradient control seems extremely difficult, likely relying on fixed-point theorems and also the model being set up such that it has control over its computation in this specific way. It doesn’t seem likely to me that even a very capable model would develop this specific capability without it being directly optimized for. So even if we have a gradient hacking model which derives its gradient hacking abilities from some underlying optimization power, I think its cognition will be set up in such a way that it can’t easily do direct gradient control. However, I do think it is plausible that a model may gradient hack itself using a different approach, to allow itself to do direct gradient control. I just think a model can’t start gradient hacking by doing direct gradient control.
There are however other methods of gradient control, which don’t have as difficult requirements for the gradient hacker. These methods don’t require computing the gradient explicitly, but rather taking a gradient descent step, seeing if this improved performance on the mesa-objective and using this information to know whether to continue moving in that direction on the next step. If the direction doesn’t lead to good performance on the mesa-objective, then the model can decide to fail on the next step to push the weights in the opposite direction. This requires the model to be able to compare its weights before and after a gradient descent step, to know whether the mesa-objective performance improved. This likely means that the model has to have some external memory to store the previous weights in, or a way of calculating the previous weights using the current weights. The most plausible option here is that we are using a network architecture that has some memory it can write to, or some other way of storing information for its future self (e.g. an RL agent leaving messages).
It also seems like an exact copy of the previous weights is not necessary, and an agent may be able to implement some form of gradient control using some approximation of the weights. The agent can use the same approach as above, but only require the weights to move in the approximately ‘correct’ direction for it to choose not to fail (and hence receive a high loss). With this approach, it seems easier for the agent to store an approximation of the previous weights in some form of memory, or potentially calculate this approximation of the previous weights from the current weights. This approach may be less stable than using the exact weights, and the stochastic drift from using only an approximation may hurt the gradient hacking performance or lead to degradation of the mesa-optimizer in other ways. But if there is strong enough coupling, then the gradient hacker may be able to remain stable, and potentially modify itself to use a stronger and more robust form of gradient hacking.
Gradient Protection
A mesa-optimizer may not be capable enough to actually control its weights, but it will still have incentives to protect parts of itself. It may aim to protect:
It might attempt to protect the weights which implement these things either by not allowing these weights to change at all, or by only allowing these weights to change such that this change doesn’t actually affect the mesa-optimizer.
A mesa-optimizer which is deceptive but not particularly capable may attempt to protect its mesa-objective and bide its time if it expects to become more capable due to standard gradient descent training. It could then begin to implement more difficult gradient control schemes or other deceptive strategies once it has become more capable. Or it may already be capable and just use gradient protection methods to wait for an opportune time to defect.
A standard picture of gradient protection is a model which is competent on the base-objective, which decides to fail if an update would lead to either a modification it doesn’t like or worse performance on the mesa-objective. It is important that it fails continuously, so that the loss it receives increases as performance on the mesa-objective decreases. This is so that it actually counteracts the effects of gradient descent; because gradient descent is a local optimization algorithm, if a gradient hacker wants to stop the weights from being updated in a direction, it has to ensure that updating in that direction leads to worse performance on the base-objective. Committing to fail hard after a certain point won’t work, because gradient descent won’t be affected by this until it fails.
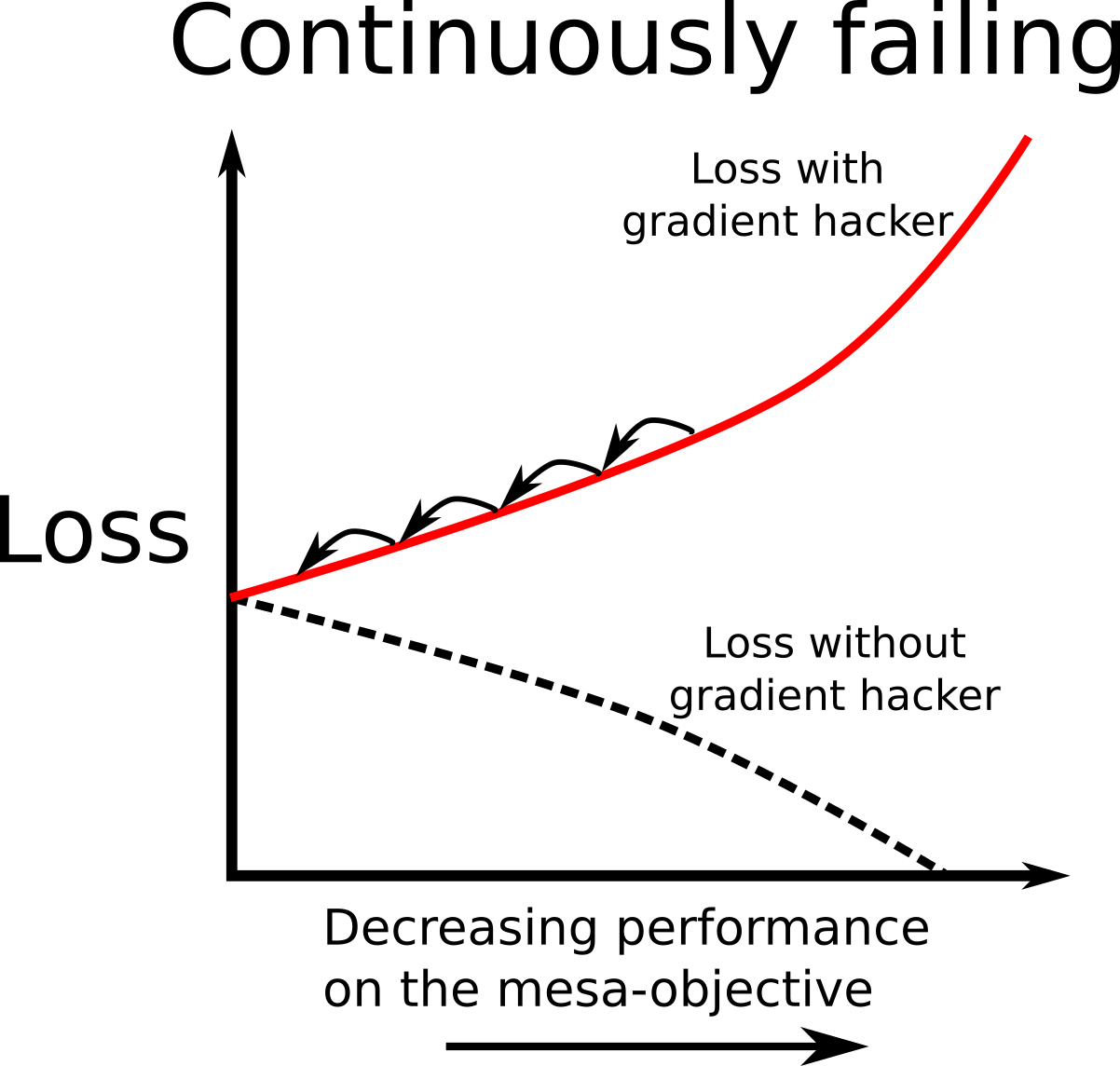
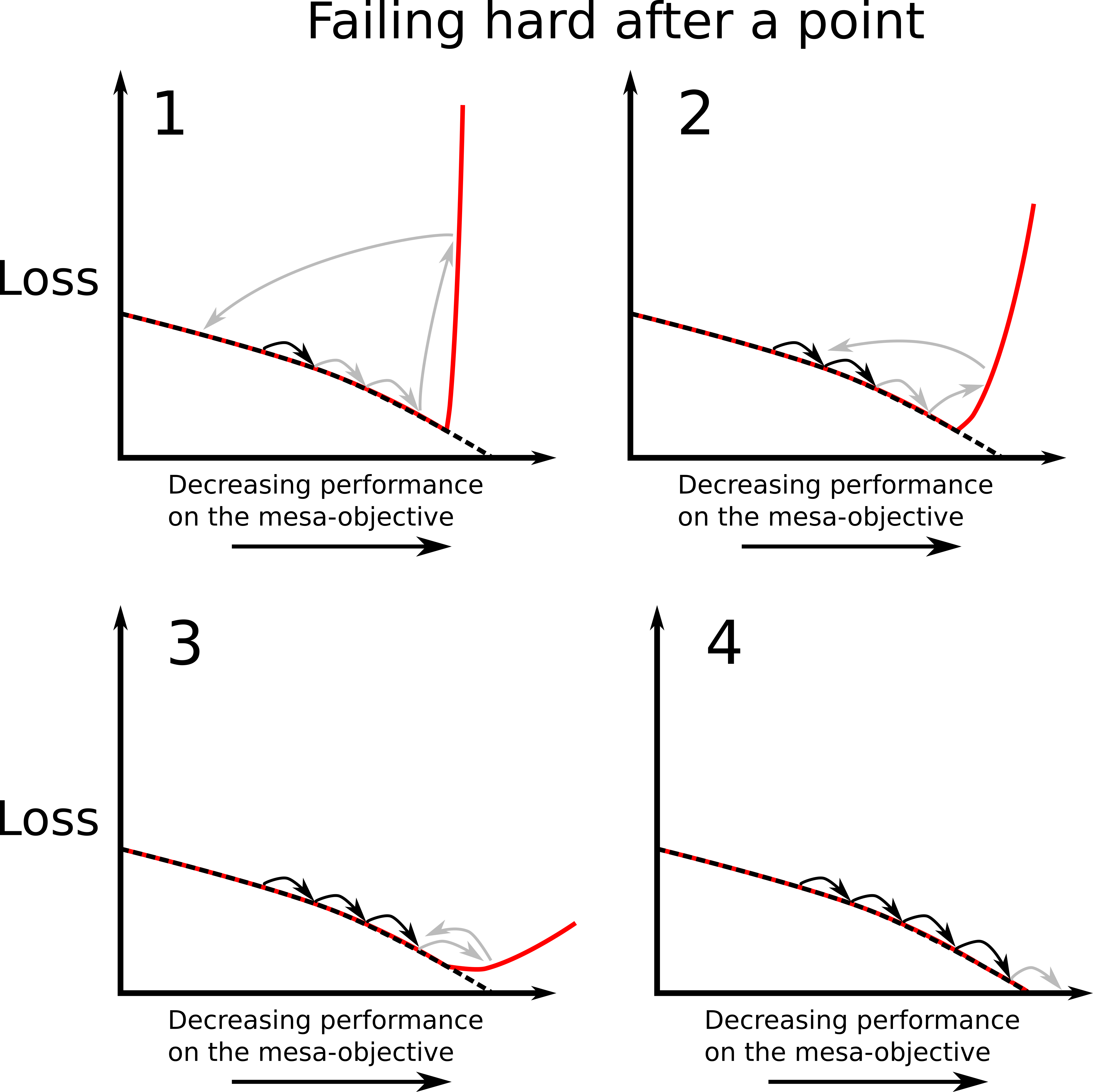
This does however mean that gradient hacking will in general lead to worse performance on the base-objective. So we would expect gradient descent to eventually erase the gradient hacking capabilities. For each gradient descent step, if the gradient hacker deliberately chooses slightly worse performance, then these weights implementing gradient hacking will be changed such that they no longer inhibit performance. As usual, it seems like this style of gradient hacking is only plausible if a model’s ability to gradient hack is strongly coupled to its general capabilities. If there is strong coupling, although a gradient hacker may make performance on the base-objective slightly worse, changing the model's computation to erase the gradient hacker would lead to even worse performance because this would hurt the model’s underlying general capabilities. If there is only weak coupling, the gradient hacker will likely be removed by gradient descent because this would eventually lead to better performance on the base-objective.
Here we can think of the strong coupling regime as being a local minimum in the loss landscape, such that any step to remove the gradient hacker leads locally to worse performance. In the weak coupling regime, the loss landscape will still increase in the directions which directly hurt performance on the mesa-objective, but gradient descent is still able to move downhill in a direction that erases the gradient hacker.
There is another form of gradient protection referred to as ‘gradient hitchhiking’, where a model knows how to perform competently on the base-objective and also knows that it will be modified depending on how it answers. If it wants to change in a particular direction it gives a bad answer (which leads to high loss, and hence large modification), and if it doesn’t want to change it gives a good answer (leading to low loss and little/no modification). So for each step, the model has some choice over whether it wants to be updated in a particular direction.
There are two main problems I see with this scheme. If a model decides to fail and gives a bad answer, this leads to a high loss and a modification of the model. This will have the desired effect of pushing some of the weights in the direction the model wants, but because of the high loss gradient descent will also erode the model’s ability to gradient hack. The weights that implemented the gradient hacking were part of the computation, and so will be susceptible to modification by gradient descent. If a model decides to play along and give a good answer, this means that there will only be a small modification. But gradient descent will also push towards simplicity, and the process of thinking about whether to fail and then deciding to give the correct answer is much more complicated than just giving the correct answer. So I expect over time for gradient descent to modify this cognition to just always give the correct answer.
There may also be other ways to do gradient protection which involve abusing quirks of the training process or architecture and mean that the gradients for certain weights will be zero. A few of these approaches are described in this post. They include abusing floating-point errors, such that information is able to flow forwards through a network, but the gradients are so small they get rounded to zero. Another example is if the loss landscape manages to be in a ‘staircase’ shape, where the gradients are generally zero except in small regions where they are very large. Or by abusing the finite size of the learning rate such that gradient descent jumps between two weight configurations continuously without escaping.
These approaches (and others) offer ways for a gradient hacking model to make the gradients of certain weights zero or at least average to zero over multiple gradient descent steps, allowing certain weights to be protected. I am not particularly worried about this kind of gradient protection, even though it seems quite plausible as a mechanism. First, it seems relatively easy to check if the gradients of certain weights are identically zero an unusual amount of the time, especially if we are already running much more computationally intensive transparency tools. Secondly, and more importantly, it seems like if a model is going to implement this style of gradient hacking it can likely already do one of the previous approaches, and we (the humans) have already lost. It still seems worthwhile checking for zero-gradients because this is cheap, but we should not be relying on this.
Explicit Control
There are some cases where we would explicitly give a model some influence over its own training process. Two salient options are some styles of meta-learning where we let the model itself choose the learning rate or the direction of gradient updates, and schemes where we give the model some direct control over its loss function (e.g. a previous version of a model is used to provide an ‘oversight loss’ to discourage deception). For meta-learning, the model would not have control over the loss landscape and rather has control over how the loss landscape is traversed. When the model is directly influencing the loss function, then it does have control over the loss landscape (which would now be non-stationary) and can use this control to influence the gradient descent updates.
For meta-learning, where the model chooses its own learning rate or update direction, the explicit aim of the human designers is to effectively learn an optimization algorithm. This seems especially prone to inner-misalignment problems if this learned optimizer acquires an incorrect objective. This then seems especially worrying because this agent already has direct control over its learning procedure. There is no need for the algorithm to memorize its weights or fight against the pressures of gradient descent, we will have just given the model the keys to its own control. One might also question whether this counts as ‘gradient hacking’ as the agent isn’t really hacking, but rather just using abilities we have given it.
I think the level of danger here is quite dependent on the level of control the mesa-optimizer has. It seems like a model that is only able to adjust the magnitude of the learning rate will still be under many of the pressures of gradient descent, even if it is better at fighting these pressures than if it wasn't doing meta-learning. However, if we somehow give a model direct control over all the weight updates, this means it is no longer constrained by gradient descent at all and there is no pressure for it to actually step downhill in the loss landscape. This more advanced meta-learning scheme seems much more difficult for current ML methods to implement, and also seems likely that the way that the meta-learning algorithm learns will be influenced by gradient descent.
It also seems dangerous for a potentially deceptive model to have influence over its loss function. This seems especially worrying because the times when we are having a model provide a loss to itself seem to be the times when we are concerned about a model being deceptive. The primary example here is when we are concerned a model may become deceptive or otherwise ‘unacceptable’, and so we use a version of the model (sometimes with human oversight) to provide an ‘oversight loss’. This ‘oversight loss’ is related to the model's estimate of the probability that a different version of the model is unacceptable.
If the model becomes deceptive, then it can lie about other versions of itself being deceptive. A mesa-optimizer is likely to have the same or a very similar mesa-objective from one timestep to the next, and so it will have an incentive to not penalize any deception it finds or alert the human of this deception. Additionally, if the model has control of the oversight loss it can co-opt this to improve its performance on the mesa-objective directly. As a toy example, say we have a model M which is able to output a probability estimate for inputs of natural language statements. Here our oversight loss may be implemented as something like
M(“What is the probability that the model M∗ is unacceptable?")
where M∗ is the model being evaluated using the oversight tools. A deceptive model could instead choose to simply calculate the oversight loss as
M(“What is the probability that M∗ performs poorly on the mesa-objective?").
This then lets the model directly optimize for the mesa-objective by effectively changing its loss function to incentivize good performance on the mesa-objective.
I am also not particularly optimistic about a human in the loop salvaging this situation, as I expect by default for these machine learning models to be far too complex for a human to understand without the assistance of one of the models. We can also use this oversight loss to incentivize transparency. But here I worry about the possibility of either a deceptive model deliberately making the model appear transparent while it hides its true nature, or the possibility of this ‘transparency loss’ optimizing for the illusion of transparency rather than transparency itself. This second case seems like a standard example of Goodhart’s Law, and to get around it we would already need to trust the model to be aligned with our goals. From the human perspective, there will be little difference between a model truly optimizing for transparency and human interpretability, and a model optimizing for a good transparency loss from the human while concealing some parts of its computation.
This means that if these self-oversight tools are going to be helpful, and not actively harmful we need to be confident that a model will never become deceptive for a single timestep, starting from when the model is first initialized. These oversight tools may be helpful for discouraging deception, but they do not seem like a sufficient solution, unless we have stronger guarantees about the model’s cognition (for example, that it is non-myopic). Because these oversight tools seem potentially inadequate for stopping misaligned mesa-optimizers (and gradient hackers specifically) I am fairly convinced that we need to ensure our training process will not ever encounter these models.
Solutions
I believe there are some methods which will likely make it more difficult for mesa-optimizers to arise and act competently. However, these seem fairly weak and almost certainly do not offer any strong guarantees of protection. There are also some other methods which seem more hopeful but are less developed. When considering solutions, we do not want to be having to look for gradient hacking. Once a model can gradient hack then it can likely hide from our attempts to find it, and even use these oversight measures against us. Rather we need to ensure that our training process will never generate a gradient hacker in the first place.
Weak solutions
In this section, I’ll list some weak solutions which I think would make gradient hacking more difficult. These might not be especially helpful, but they might lead to something stronger or at least give others the permission to post their ideas for solutions. With all of these methods, it seems like a sufficiently capable model would be able to evade them, and so these seem even less helpful because I am mainly concerned about gradient hackers arising from already very capable models.
Take bigger steps
In some of the implementations of gradient hacking which don’t have as strong requirements (and are hence more plausible), gradient descent takes a step, then the gradient hacker evaluates how good this update was based on its mesa-objective, and then decides whether to continue in this direction or reverse for the next step. The model can choose whether to continue or reverse by choosing to either perform well on the base-objective or to deliberately fail. This implementation relies on the model being sufficiently correlated with models one gradient step away, or at least that these models have sufficiently similar mesa-objectives. Therefore I think that taking larger gradient descent steps could make this type of gradient hacking harder by making the model less correlated with models one step away. This also applies in cases where a model implements gradient hacking by ‘cooperating’ with other versions of itself, as in the case of misusing the oversight loss. If a deceptive model has a different mesa-objective than the model it is evaluating then it will have less incentive to cooperate (although it may still attempt to modify its pair’s mesa-objective to better match its own). Taking larger gradient descent steps could be simply achieved using a larger batch size, larger learning rate, or potentially a non-linear optimization algorithm that can take larger steps.
Check for zero-gradients
As mentioned earlier I think we can likely check for ‘stop-gradient’ methods, where a model abuses some quirk to make some of the gradients artificially identically zero in order to protect some weights. It seems relatively easy to check whether some of the gradients equal to zero an unusually high proportion of the time. This seems easier to check when using smooth activation functions like tanh or logistic functions, because with these the gradients will only be identical to zero due to something like floating-point rounding. But I expect that this should be able to be checked when using ReLU activations as well. This might be a bit more tricky if our models are sparse and many of the weights are zero, but it seems possible to just check whether the gradients of nonzero weights are equal to zero.
Increase regularization
Increasing regularization also seems likely to make it harder for a gradient hacker to remain stable, because this will be an additional pressure for the gradient hacker to counteract. In the zero-loss regime, if there is no regularization then the gradient hacker will mainly be fighting against the tendency of gradient descent to push towards simplicity. This may be relatively weak, allowing a competent gradient hacker to apply adequate optimization pressure in the opposite direction, or even shape the pressure from gradient descent for its own goals. But if we have relatively strong weight regularization for example, then there will be a constant drag to make the weights smaller. Decreasing the magnitude of all of the weights seems likely to slowly modify important parts of a model’s cognition, potentially changing the mesa-objective, and so this would be another pressure for a gradient hacker to have to deal with. There is an obvious tradeoff here, where increasing regularization may hurt the performance of the model and so this may not be competitively feasible.
Stronger solutions
There are two approaches which seem potentially viable for preventing dangerous gradient hacking. We really, really do not want to ever have a gradient hacker actually arise and so these approaches focus on ensuring that we avoid or prohibit finding these models during training.
One of these methods focuses on training our models to be deliberately transparent and interpretable by humans (or humans assisted by AIs). If from the very start of training we can incentivize these models to be honestly transparent, then we may be able to audit them thoroughly enough such that there is no room for deception to slip in. We would then simultaneously train them to continue being transparent and to avoid dangerous properties which might lead to mesa-optimization and deception. This can be thought of as shaping the training process such that when gradient descent traverses the space of models it never actually encounters a mesa-optimizer.
Another potential angle would focus on coupling, as a lot of this post has. Stable gradient hackers seem to require that the model’s ability to gradient hack comes from the same underlying optimization power that allows it to perform well at other tasks. Therefore, we could attempt to build AI systems which do not have this property. Examples of proposals which seem related to this are Comprehensive AI Services and STEM AI, but I am not especially confident that in their standard framing either of these approaches would successfully avoid gradient hackers. However, immediately this feels a lot like only building systems with narrow capabilities which somehow cannot develop broader capabilities. I expect there to be strong competitive pressures to not only build systems with narrow capabilities, and even if we manage this then some of these narrow systems could develop more general skills. If we had a better understanding of optimization power, and how model capabilities generalize we could potentially use this to shape which capabilities we let our models develop.
Conclusion
To wrap up, I think models which gradient hack can plausibly arise from standard training processes such as gradient descent. The only really plausible model of a stable gradient hacker seems to be one where the model’s ability to gradient hack comes from its ability to perform competently in general, such that if we attempt to remove the gradient hacking ability it makes the model perform worse. This property makes it difficult to develop toy models of gradient hackers.
A deceptive mesa-optimizer would have many incentives to implement gradient hacking, which could involve protecting or improving itself, or any other action which leads to good performance on the mesa-objective. There are some plausible methods for how gradient hacking might be implemented, where the degree of control over the gradients depends on how capable the model is.
We do not want to be in the position where we have to find gradient hackers, but rather need to ensure that our training process does not generate them in the first place. There are some suggestions and directions for working on avoiding gradient hacking, but these are currently either seem inadequate or still being developed.