This post is part of my hypothesis subspace sequence, a living collection of proposals I'm exploring at Refine. Preceded by an interlude.
Thanks Adam Shimi, @artaxerxes, Herbert Jaeger, Tamsin Leake, and Ze Shen for discussion informing this post.
Intro
In the previous post, I explored a grammar of alignment proposals based on (what I later learned could be referred to as) coupled dynamical systems. To help you get a sense of this view, one family of proposals tackles the alignment problem by having human researchers optimize a trainer (e.g. oversight leagues) which optimizes a trainer (e.g. SGD across model space employing empirical risk as heuristic) which optimizes a model (e.g. LLM) which optimizes a world (e.g. text). Other families have different numbers of optimization levels (e.g. True Name partially obviates the need for trainer), integrate feedback loops (e.g. human amplification), or extend the optimization stack in some other way. In this, the focus moves from what to point an AI at, to how to move towards the associated trainer state (e.g. using heuristics across trainer space and above, similar to empirical risk as heuristic across model space). A shift from targets to processes for reaching said targets.
From this level of abstraction, one can identify issues which systematically plague entire families of proposals. For instance, there's still a bounded human at the top guiding downstream optimization (e.g. on trainer). In the current post, I aim to explore how two notions from dynamical systems apply at different levels of optimization, and how those might help alleviate systematic issues. The two notions are:
- Stability. A region of the state space of a dynamical system is deemed stable if slight perturbations to objects in that region don't result in the object permanently leaving the region. For instance, a tiny asteroid which crashes into Earth won't cause Earth to leave its orbit around the Sun, because Earth's orbit is stable. In contrast, the smallest gust of wind blowing on a pencil balanced on its tip will cause it to leave that region of state space behind, as it's not stable. Note: While stability is mathematically defined only for such regions of state space, I'll stretch the term "stable" for the purpose of this post to also describe the dynamical system which in turn contains reachable stable solutions. This reading of stability can also be described as "the region of plausible initial conditions is contained within the basin of attraction of a single attractor." I purposefully avoided the related reading of "sensitive to initial conditions" due to its chaotic connotations.
- Structural Stability. While the previous property touches mostly on perturbations of objects inhabiting a state space, structural stability touches on perturbations of the dynamical system itself. For instance, the map "implemented" by the laws of physics across world states would be deemed structurally stable if slight changes in the values of fundamental physical constants wouldn't radically change the states towards which the world converges. You might still get planets orbiting around stars making up galaxies. In contrast, if the laws of physics across world states would turn out not to be structurally stable, the slightest change to the fundamental physical constants would yield radically unfamiliar universes.
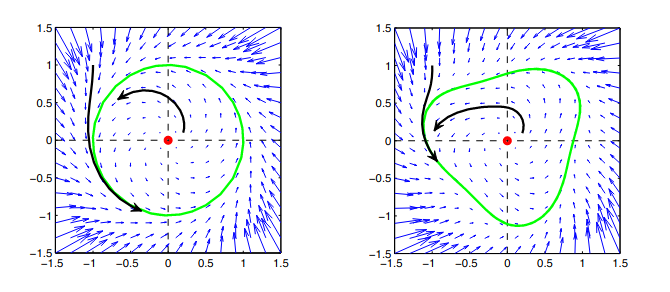
Instances
1. Model
Let's explore the notions of stability and structural stability in the context of different levels of the optimizer stack. First, if a model is stable (according to the stretched definition), then the particular state the world is initially in doesn't have much of an influence on the state of the world the world will get in through its optimization. For instance, the fine-tuned version of VPT can spawn in a random Minecraft world and bring it in a state in which it possesses a diamond pickaxe. The attractor could be seen as a high-dimensional manifold of worlds-where-I-have-a-diamond-pickaxe. Alternatively, a prompted DALL-E can start with any noisy image and reliably optimize it towards being meaningful. Sure, there is some path dependency, in that DALL-E strikes the manifold from different angles and yields slight variations, but overall it's pretty stable.



Now, what about structural stability at the model level? Do slight perturbations to the model parametrization itself lead to qualitatively different behavior? Dropout and DropConnect are two instances of such perturbations, where a tiny proportion of either nodes or edges in the scalar version of the computational graph of an ML model get mutated. In practice, while Dropout and DropConnect do reduce performance slightly (during training, as they're usually disabled during inference), it's often not a big hit, especially as the model's trainer gradually moves it towards parametrizations which are structurally stable (e.g. states from which a 0.3-Dropout sway across model space doesn't hurt empirical risk much).
II. Trainer
Let's now go a step above and explore the same two notions in the context of the trainer. What does it mean for a trainer to be stable? Well, a stable trainer should be able to take in model parametrizations scattered across model space and reliably move them towards high-performance states. Given the fact that virtually all training procedures start with a random initialization of model parameters, most trainers can be described as quite stable, as they can reliably take in random parametrizations and optimize them successfully. Even when a model has internalized very particular dynamics during a previous training stage, subsequent training on a different task can unfortunately make away with all that complexity via catastrophic forgetting and efficiently repurpose representational resources for solving the present task.
Now, what about the structural stability of trainers? Do slight variations in the hyperparameters which define them (e.g. learning rate, dataset informing hill-climbing heuristics) lead to qualitatively different behavior downstream? An interesting talking point here is momentum, which seems to significantly broaden the range of learning rates which enable good trainer performance. In a sense, this feature crafted into the trainer from a level above by the human researcher improves its structural stability. It doesn't matter that much what learning rate settings you plug in then, as the trainer still behaves in a similar way.
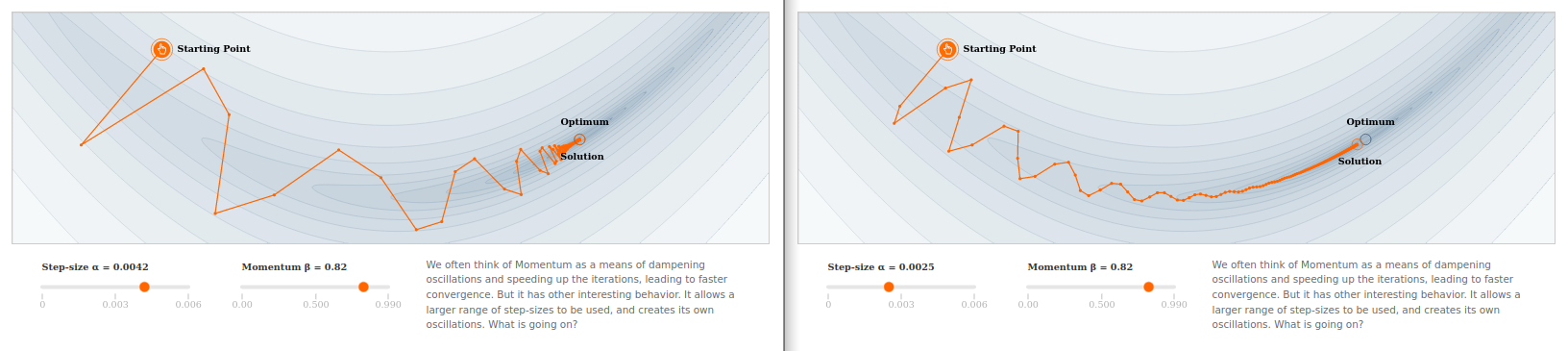
III. Trainer
Let's now explore the two notions in the context of the trainer. If an oversight league as a trainer was stable, then the particular positive examples specified by humans might not be that impactful on the resulting trainer. If an ideological inference engine as a trainer was stable, then the small print of the seed knowledge base specified by humans might not be that impactful on the resulting trainer being crafted. If representational tethers were to be stable, then the initial conceptual framework employed by the ML model would be washed out. If CIRL were to, the agent's initial estimate of the human objective would be transient. If PreDCA were to, the system's initial candidates for precursors and their objectives wouldn't influence the final solutions much.
Right, and how about structural stability? Do tiny changes in those proposals lead to qualitatively different effects across the optimizer stack? Here I lack existing instances of such variations, but again the presence of structural stability would make the exact choice of trainer implementation details relatively inconsequential.
IV. Human
How about the human researchers optimizing the trainer? A stable researcher (in the same sense as above) would be able to start with a largely arbitrary version of a trainer before being able to successfully move it towards a state which exhibits good downstream performance. In contrast, an unstable researcher (again try to suspend connotations) would be driven more by path-dependence in their search across trainer space, rather than leaving the idiosyncratic initial conditions behind and converging towards suitable trainer trainers.
Predictably, structural stability of a researcher would describe the limited influence of perturbations to their method of downstream optimization. Slightly different versions of them might end up optimizing the trainer in the same way. Methodological therapy might need to be particularly strong a perturbation in order to have an effect in the case in which researchers are structurally stable. However, this need not be the case, as researchers might themselves cross bifurcation points and radically change their approach to optimization.
(Structural) Stability & Alignment
While it's certainly satisfying to find such patterns — especially when recursively nested as in the case of optimizer stacks — where does that lead us in terms of making progress on the alignment problem?
Measuring Stability
We might be interested in developing trainer trainers which consistently nudge trainers towards the same kinds of trainers, similar to how DALL-E nudges images towards the same kinds of images. However, a trainer which simply nudges trainers towards the same outcomes isn't equivalent to a trainer which nudges trainers towards good trainers in particular. That said, I think good trainer trainers (i.e. those which can find trainers which produce aligned models) are more likely to lead to consistent kinds of trainers than bad trainer trainers, similar to how a simplicity heuristic might be handy in crossing things off. This intuition is based on the observation that human values appear relatively stable across time and space (though cultural and trainer fields might not necessarily be close). Western and Eastern cultures are unlikely to casually swap ideologies from one decade to the next. A slight memetic sway across the US is unlikely to prevent it from coming back to its mainstream ideals soon after. In contrast, if invoking the Anna Karenina principle, disturbed versions of human values are unlikely to form large unified basins of attraction, because they'd be fundamentally incompatible with each other. In other words, the stability of a region in trainer space might slightly conditionally boost the probability that said region leads to aligned models.
Given this, how could we measure the stability of a trainer? In order to see whether different initial states consistently get nudged towards a tightly-knit region of trainer space, we could... simply try running a trainer on different initial trainers and measure the spread of the result. Bootstrapping (stats sense) the dataset used for informing hill-climbing heuristics across model space might be an easy way to achieve that sampling of trainers for certain proposals. For instance, one could try to sample-with-replacement the initial positive examples used to kickstart an oversight league, and get different evaluators at the end, where each evaluator could be incorporated into unique trainers as a heuristic for navigating model space. Alternatively, one could try to "wiggle" the initial trainer across specific dimensions and sample initial conditions this way. For instance, one could try to systematically paraphrase parts of the seed knowledge base in ideological knowledge engines and see whether the inference algorithm takes the variants towards wildly different places.
The "start with different inits and see how things go collectively" can be visualized as ensembles across state space being swayed around in unison as deformed areas, as opposed to single individual points moving around:
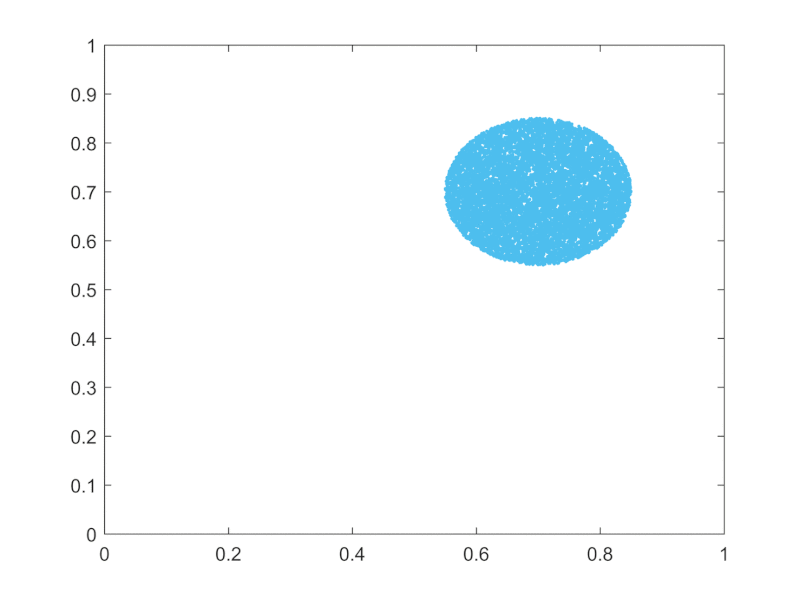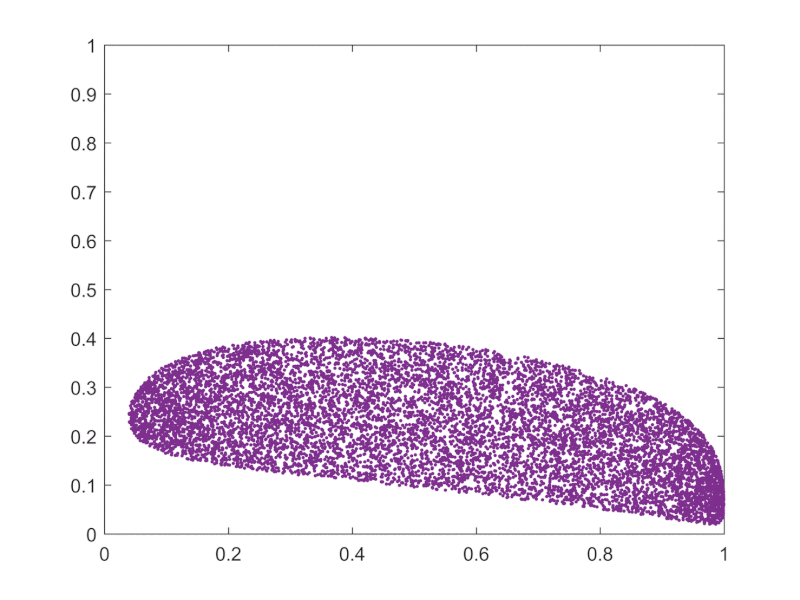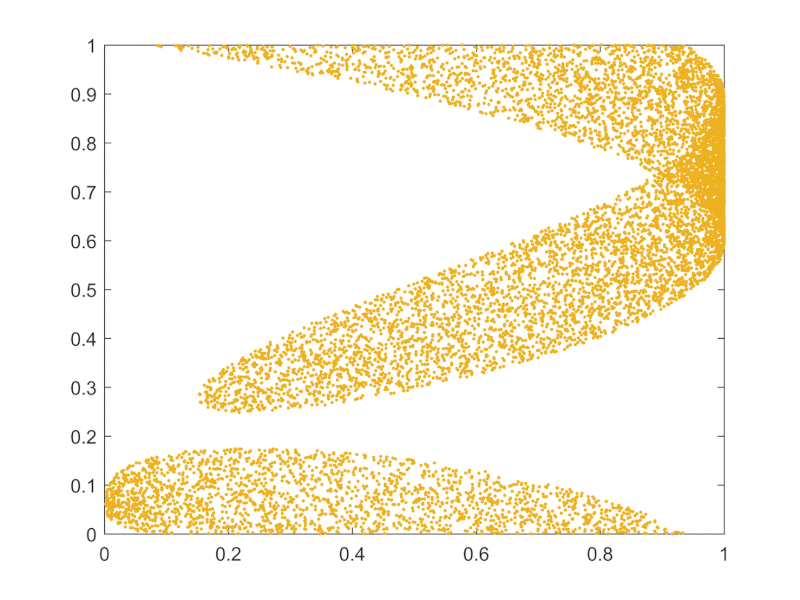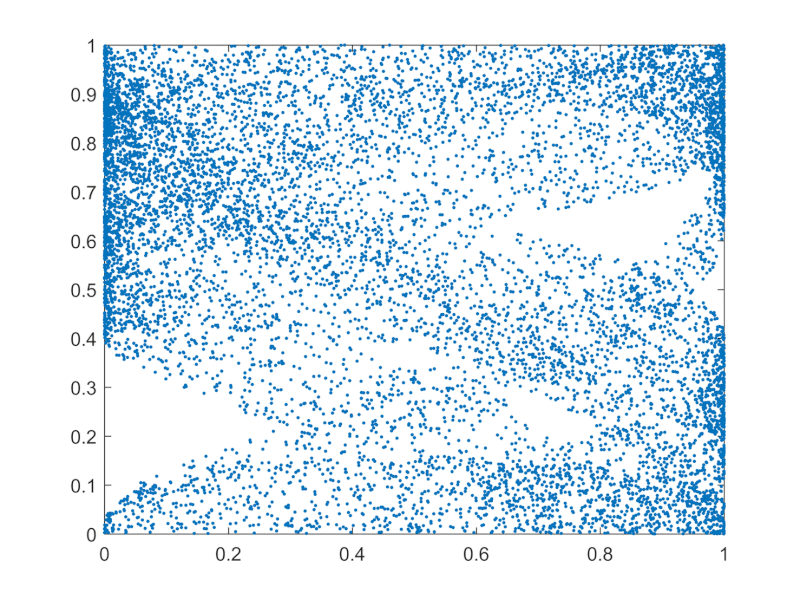
But say we tried running a trainer forward starting with different initial trainers. We got a set of optimized trainers. How do we actually gauge whether they populate the same region in trainer space? For instance, it is non-trivial to infer whether the different variants of the "Girl with a Pearl Earring" painting generated by DALL-E share family resemblence. In terms of pixel-wise distances, the images are quite different, so what brings them together? We might consider the two trainers similar if they bring about structurally stable models, and in doing so tackle challenges of measuring one kind of stability with another. Fortunately, the problem is defined somewhat better for models. For instance, the KL-divergence across output distributions of two different models in a shared context is often used as a proxy for the distance between the two dynamics being implemented. It's decently successful in keeping a model being fine-tuned on a meaningful "leash" from its original location, so that it doesn't deviate too much, as seen in RLHF.
Unfortunately, KL-divergence is naively used as a measure of difference between two fields across world space at a specific location. "Starting in this given world state, how do those two models take it from here?" Sampling contexts across the entirety of world space would be intractable as a way of establishing the similarity of two models. There could always be hidden edge cases where the two radically disagree. Here's a glimmer of how one mighy efficiently measure how much two ML-implemented fields agree at every location across world state at once, maybe. First, compose the two models into a larger computational graph, where the same input feeds into both, and their outputs feed into a difference operator. Second, optimize the input, rather than the model, so that it elicits a high difference, similar to DeepDream or contrastive dreaming. Third, try to analogize the provable criteria used in robust ML in order to get definitive bounds on the difference between models at any given point without sampling. Even crazier, it might be possible to also obtain bounds on field differences at levels above the model, assuming differentiability. For instance, the future exploitation of oversight leagues hints at being able to differentiate through trainer training itself. Ditto for learning to learn by gradient descent by gradient descent (G.pt anyone?). Those are currently very rough thoughts.
There's also an anthropic angle on this whole gauging of stability thing. If we can reasonably bootstrap (stats sense again) our way towards the distribution of initial conditions we might have started optimization with and we analyze the nature of possible outcomes resulting from those, how should that influence our particular choice of seed in high-stakes runs? What if we stick to the majority of seeds approaching a shared region together? If that stable outcome actually turns out to be inappropriate, whole timelines hopping on the stability train would go south, for instance.
Improving Stability
Propagating an ensemble of trainers through the ebbs and flows exerted by the trainer might give us a sense of how reliably it nudges towards a consistent region. This might allow for the ranking of different hand-crafted designs of trainer trainers, assuming that's where the human-artificial interface lies in the optimization stack. However, besides being able to compare trainer trainers with different architectures, measuring stability might also enable the systematic improvement of a given trainer in that sense.
If stability is defined here as the containment of plausible initial conditions in a basin of attraction across trainer space, then selecting the initial conditions themselves might provide a relevant degree of freedom. Concretely, if perturbations of initial conditions along certain dimensions are more likely to interfere with the convergence of solutions than others, then it might make sense to focus human optimization on those aspects of the seed to which the trainer is particularly sensitive to. For instance, if paraphrased variations of a certain dictum included in the seed knowledge base of an ideological inference engine cause important variations in the expanded versions, then it might be useful to focus human optimization on specifying it well, rather than some less brittle ones. Similarly, if the exclusion of certain kinds of samples in the dataset used to kickstart an oversight league cause a high spread of outcomes, it might perhaps be useful to focus on documenting it more extensively. In other words, conducting a sensitivity analysis on the trainer might enable active-learning on its part, where human feedback could be requested to optimally reduce uncertainty in the nature of the trainers being approached through trainer training.
However, there might also be issues with selecting for trainer trainers which consistently get us a certain type of trainers. A stable region of trainers obtained through trainer training might be tied to value lock-in in the models yielded downstream, a situation in which human meta-values would be compatible with object-level ones shifting around, but in which the trainer trainer wouldn't succeed in enabling that shift. Yet another issue is that the very extension of the optimizer stack upwards comes with an inevitable trade-off between unfortunate human-model distancing and fortunate aiding of base-level implementation (similar to hand-crafting GPT-3 versus employing a trainer to navigate model space using heuristics). The framing shifts the problem from localization of aligned regions across model space to means of gradually reaching said regions, in the hope that specifying guidance (e.g. vector fields across spaces) might be more feasible than specifying targets. In this context, the two notions of stability are meant to help select guidance systems (i.e. find trainer trainers). However, we might also stumble across dangerous territory in the process of reaching desired targets.
Outro
Organizing proposals through the lens of coupled optimizers surfaces systematic issues. For instance, there's still a bounded human at the top guiding downstream optimization (e.g. on trainer). Exploring how classic notions from coupled dynamical systems translate to alignment might help uncover systematic solutions through (1) provable guarantees of stability (e.g. getting bounds on stability of trainer), and (2) active-learning procedures making optimal use of human optimization in reducing model uncertainty.