All of Vivek Hebbar's Comments + Replies

Do you want to try playing this game together sometime?

We're then going to use a small amount of RL (like, 10 training episodes) to try to point it in this direction. We're going to try to use the RL to train: "Act exactly like [a given alignment researcher] would act."

Why are we doing RL if we just want imitation?  Why not SFT on expert demonstrations?
Also, if 10 episodes suffices, why is so much post-training currently done on base models?

If the agent follows EDT, it seems like you are giving it epistemically unsound credences. In particular, the premise is that it's very confident it will go left, and the consequence is that it in fact goes right. This was the world model's fault, not EDT's fault. (It is notable though that EDT introduces this loopiness into the world model's job.)

The idea of dividing failure stories into "failures involving rogue deployments" and "other failures" seems most useful if the following argument goes through:
1. Catastrophes require a very large (superhuman?) quantity and/or quality of intellectual labor
2. Either this labor is done by AIs in approved scaffolds, or it is done in "rogue deployments"
3. Hence the only easy-by-default disaster route is through a rogue deployment
4. Hence if we rule out rogue deployments and very impressive/difficult malicious labor in our scaffolds, we are safe

This seems true f... (read more)

This google search seems to turn up some interesting articles (like maybe this one, though I've just started reading it).

Paul [Christiano] called this “problems of the interior” somewhere

Since it's slightly hard to find: Paul references it here (ctrl+f for "interior") and links to this source (once again ctrl+f for "interior").  Paul also refers to it in this post.  The term is actually "position of the interior" and apparently comes from military strategist Carl von Clausewitz.

Note: The survey took me 20 mins (but also note selection effects on leaving this comment)

Here's a fun thing I noticed:

There are 16 boolean functions of two variables.  Now consider an embedding that maps each of the four pairs {(A=true, B=true), (A=true, B=false), ...} to a point in 2d space.  For any such embedding, at most 14 of the 16 functions will be representable with a linear decision boundary.

For the "default" embedding (x=A, y=B), xor and its complement are the two excluded functions.  If we rearrange the points such that xor is linearly represented, we always lose some other function (and its complement).  In fact... (read more)

Oops, I misunderstood what you meant by unimodality earlier. Your comment seems broadly correct now (except for the variance thing). I would still guess that unimodality isn't precisely the right well-behavedness desideratum, but I retract the "directionally wrong".

The variance of the multivariate uniform distribution $U\left(\right[0,1]\times [0,1\left]\right)$ is largest along the direction $x_1+x_2$, which is exactly the direction which we would want to represent a AND b.

The variance is actually the same in all directions.  One can sanity-check by integration that the variance is 1/12 both along the axis and along the diagonal.

In fact, there's nothing special about the uniform distribution here: The variance should be independent of direction for any N-dimensional joint distribution where the N constituent distributions are ind... (read more)

Maybe models track which features are basic and enforce that these features be more salient

Couldn't it just write derivative features more weakly, and therefore not need any tracking mechanism other than the magnitude itself?

When you describe the "emailing protein sequences -> nanotech" route, are you imagining an AGI with computers on which it can run code (like simulations)?  Or do you claim that the AGI could design the protein sequences without writing simulations, by simply thinking about it "in its head"?

It would still be interesting to know whether you were surprised by GPT-4's capabilities (if you have played with it enough to have a good take)

POV: I'm in an ancestral environment, and I (somehow) only care about the rewarding feeling of eating bread. I only care about the nice feeling which comes from having sex, or watching the birth of my son, or being gaining power in the tribe. I don't care about the real-world status of my actual son, although I might have strictly instrumental heuristics about e.g. how to keep him safe and well-fed in certain situations, as cognitive shortcuts for getting reward (but not as terminal values). 

Would such a person sacrifice themselves for their children (in situations where doing so would be a fitness advantage)?

Any idea why "cheese Euclidean distance to top-right corner" is so important?  It's surprising to me because the convolutional layers should apply the same filter everywhere.

Agreed.  To give a concrete toy example:  Suppose that Luigi always outputs "A", and Waluigi is {50% A, 50% B}.  If the prior is {50% luigi, 50% waluigi}, each "A" outputted is a 2:1 update towards Luigi.  The probability of "B" keeps dropping, and the probability of ever seeing a "B" asymptotes to 50% (as it must).

This is the case for perfect predictors, but there could be some argument about particular kinds of imperfect predictors which supports the claim in the post.

In section 3.7 of the paper, it seems like the descriptions ("6 in 5", etc) are inconsistent across the image, the caption, and the paragraph before them.  What are the correct labels?  (And maybe fix the paper if these are typos?)

In ML terms, nearly-all the informational work of learning what “apple” means must be performed by unsupervised learning, not supervised learning. Otherwise the number of examples required would be far too large to match toddlers’ actual performance.

I'd guess the vast majority of the work (relative to the max-entropy baseline) is done by the inductive bias.

As I understand Vivek's framework, human value shards explain away the need to posit alignment to an idealized utility function. A person is not a bunch of crude-sounding subshards (e.g. "If food nearby and hunger>15, then be more likely to go to food") and then also a sophisticated utility function (e.g. something like CEV). It's shards all the way down, and all the way up.^[10] 

This read to me like you were saying "In Vivek's framework, value shards explain away .." and I was confused.  I now think you mean "My take on Vivek's is that value s... (read more)

Makes perfect sense, thanks!

"Well, what if I take the variables that I'm given in a Pearlian problem and I just forget that structure? I can just take the product of all of these variables that I'm given, and consider the space of all partitions on that product of variables that I'm given; and each one of those partitions will be its own variable.

How can a partition be a variable?  Should it be "part" instead?

ETA: Koen recommends reading Counterfactual Planning in AGI Systems before (or instead of) Corrigibility with Utility Preservation

Update: I started reading your paper "Corrigibility with Utility Preservation".^[1]  My guess is that readers strapped for time should read {abstract, section 2, section 4} then skip to section 6.  AFAICT, section 5 is just setting up the standard utility-maximization framework and defining "superintelligent" as "optimal utility maximizer".

Quick thoughts after reading less than half:

AFAICT,^[2] this is a mathematica... (read more)

To be more specific about the technical problem being mostly solved: there are a bunch of papers outlining corrigibility methods that are backed up by actual mathematical correctness proofs

Can you link these papers here?  No need to write anything, just links.

1. Try to improve my evaluation process so that I can afford to do wider searches without taking excessive risk.

Improve it with respect to what?  

My attempt at a framework where "improving one's own evaluator" and "believing in adversarial examples to one's own evaluator" make sense:

• The agent's allegiance is to some idealized utility function $U_{ideal}$ (like CEV).  The agent's internal evaluator $Eval$ is "trying" to approximate $U_{ideal}$ by reasoning heuristically.  So now we ask Eval to evaluate the plan "do argmax w.r.t

Yeah, the right column should obviously be all 20s.  There must be a bug in my code^[1] :/

I like to think of the argmax function as something that takes in a distribution on probability distributions on $W$ with different sigma algebras, and outputs a partial probability distribution that is defined on the set of all events that are in the sigma algebra of (and given positive probability by) one of the components.

Take the following hypothesis $h_3$:

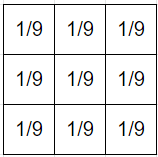
If I add this into $P$ with weight ${10}^{-9}$, then the middle column is still near... (read more)

Now, let's consider the following modification: Each hypothesis is no longer a distribution on $W$, but instead a distribution on some coarser partition of $W$. Now ${\text{argmax}}_{Q\in \Delta W}{G}_{h\sim P}{G}_{w\sim h}Q\left(w\right)$ is still well defined

Playing around with this a bit, I notice a curious effect (ETA: the numbers here were previously wrong, fixed now):

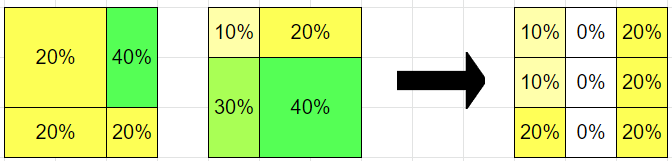
The reason the middle column goes to zero is that hypothesis A puts 60% on the rightmost column, and hypothesis B puts 40% on the leftmost, and neither cares about the middle column specifically.

But philosophically, what d... (read more)

A framing I wrote up for a debate about "alignment tax":

1. "Alignment isn't solved" regimes:
   1. Nobody knows how to make an AI which is {safe, general, and broadly superhuman}, with any non-astronomical amount of compute
   2. We know how to make an aligned AGI with 2 to 25 OOMs more compute than making an unaligned one
2. "Alignment tax" regimes:
   1. We can make an aligned AGI, but it requires a compute overhead in the range 1% - 100x.  Furthermore, the situation remains multipolar and competitive for a while.
   2. The alignment tax is <0.001%, so it's not a concern.
   3. The leadi

If the system is modular, such that the part of the system representing the goal is separate from the part of the system optimizing the goal, then it seems plausible that we can apply some sort of regularization to the goal to discourage it from being long term.

What kind of regularization could this be?  And are you imagining an AlphaZero-style system with a hardcoded value head, or an organically learned modularity?

• Pr π∈ξ [U(⌈G⌉,π) ≥ U(⌈G⌉,G*)] is the probability that, for a random policy π∈ξ, that policy has worse utility than the policy G* its program dictates; in essence, how good G's policies are compared to random policy selection

What prior over policies?

given g(G|U), we can infer the probability that an agent G has a given utility function U, as Pr[U] ∝ 2^-K(U) / Pr π∈ξ [U(⌈G⌉,π) ≥ U(⌈G⌉,G*)]) where ∝ means "is proportional to" and K(U) is the kolmogorov complexity of utility function U.

Suppose the prior over policies is max-entropy (uniform over all action seq... (read more)

I have seen one person be surprised (I think twice in the same convo) about what progress had been made.

ETA: Our observations are compatible.  It could be that people used to a poor and slow-moving state of interpretability are surprised by the recent uptick, but that the absolute progress over 6 years is still disappointing.

All in all, I don't think my original post held up well.  I guess I was excited to pump out the concept quickly, before the dust settled.  Maybe this was a mistake?  Usually I make the ~opposite error of never getting around to posting things.

The perspective and the computations that are presented here (which in my opinion are representative of the mathematical parts of the linked posts and of various other unnamed posts) do not use any significant facts about neural networks or their architecture.

You're correct that the written portion of the Information Loss --> Basin flatness post doesn't use any non-trivial facts about NNs.  The purpose of the written portion was to explain some mathematical groundwork, which is then used for the non-trivial claim.  (I did not know at the time ... (read more)

Note that, for rational *altruists* (with nothing vastly better to do like alignment), voting can be huge on CDT grounds -- if you actually do the math for a swing state, the leverage per voter is really high.  In fact, I think the logically counterfactual impact-per-voter tends to be lower than the impact calculated by CDT, if the election is very close. 

Exciting work!  A minor question about the paper:

Does this mean that it writes a projection of S1's positional embedding to S2's residual stream?  Or is it meant to say "writing to the position [residual stream] of [S2]"?  Or something else?

falls somewhere between 3rd and 10th place on my list of most urgent alignment problems to fix

What is your list of problems by urgency, btw?  Would be curious to know.

From this paper, "Theoretical work limited to ReLU-type activation functions, showed that in overparameterized networks, all global minima lie in a connected manifold (Freeman & Bruna, 2016; Nguyen, 2019)"

So for overparameterized nets, the answer is probably:

• There is only one solution manifold, so there are no separate basins.  Every solution is connected.
• We can salvage the idea of "basin volume" as follows:
  • In the dimensions perpendicular to the manifold, calculate the basin cross-section using the Hessian.
  • In the dimensions parallel to the manifol

The loss is defined over all dimensions of parameter space, so $L\left(x\right)=x_1^2+x_2^2$  is still a function of all 3 x's.  You should think of it as $L\left(x\right)=x_1^2+x_2^2+0x_3^2$.  It's thickness in the $x_3$ direction is infinite, not zero.

Here's what a zero-determinant Hessian corresponds to:

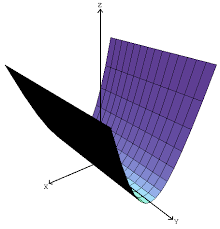
The basin here is not lower dimensional; it is just infinite in some dimension.  The simplest way to fix this is to replace the infinity with some large value.  Luckily, there is a fairly principled way to do this:

1. Regularization / weight decay prov

I will split this into a math reply, and a reply about the big picture / info loss interpretation.

Math reply:

Thanks for fleshing out the calculus rigorously; admittedly, I had not done this.  Rather, I simply assumed MSE loss and proceeded largely through visual intuition.  

I agree that assuming MSE, and looking at a local minimum, you have $rank\left(Hess\right(L\left)\right)=rank\left(Jf\right)$

This is still false!  Edit: I am now confused, I don't know if it is false or not.  

You are conflating ${\nabla }_{f}l\left(f\right(\theta \left)\right)$ and ${\nabla }_{\theta }l\left(f\right(\theta \left)\right)$.  Adding disa... (read more)

Thanks for this reply, its quite helpful.

I feel it ought to be pointed out that what is referred to here as the key result is a standard fact in differential geometry called (something like) the submersion theorem, which in turn is essentially an application of the implicit function theorem.

Ah nice, didn't know what it was called / what field it's from.  I should clarify that "key result" here just meant "key result of the math so far -- pay attention", not "key result of the whole post" or "profound/original".

The Jacobian matrix is what you call 

I'm pretty sure my framework doesn't apply to grokking.  I usually think about training as ending once we hit zero training loss, whereas grokking happens much later.

I'll reply to the rest of your comment later today when I have some time

About the contours:  While the graphic shows a finite number of contours with some spacing, in reality there are infinite contour planes and they completely fill space (as densely as the reals, if we ignore float precision).  So at literally every point in space there is a blue contour, and a red one which exactly coincides with it.

Yup, seems correct.

Yeah, this seems roughly correct, and similar to what I was thinking.  There is probably even a direct connection to the "asymptotic equipartitioning" math, via manifold counts containing terms like "A choose B" from permutations of neurons.

Yep, I am assuming MSE loss generally, but as you point out, any smooth and convex loss function will be locally approximately quadratic.  "Saddle points all the way down" isn't possible if a global min exists, since a saddle point implies the existence of an adjacent lower point.  As for asymptotes, this is indeed possible, especially in classification tasks.  I have basically ignored this and stuck to regression here.  

I might return to the issue of classification / solutions at infinity in a later post, but for now I will say this: &... (read more)

Is the claim here that the 2^200 "persuasive ideas" would actually pass the scrutiny of top human researchers (for example, Paul Christiano studies one of them for a week and concludes that it is probably a full solution)?  Or do you just mean that they would look promising in a shorter evaluation done for training purposes?

Oh, this is definitely not what I meant.

"Betting odds" == Your actual belief after factoring in other people's opinions

"Inside view" == What your models predict, before factoring in other opinions or the possibility of being completely wrong

Checked; the answer is no: https://www.lesswrong.com/posts/Lq6jo5j9ty4sezT7r/teaser-hard-coding-transformer-models?commentId=ET24eiKK6FSJNef7G

Nice!  Do you know if the author of that post was involved in RASP?

What probability do you assign to the proposition "Prosaic alignment will fail"?

1. Purely based on your inside view model
2. After updating on everyone else's views

Same question for:

 "More than 50% of the prosaic alignment work done by the top 7 researchers is nearly useless"