All of the experimental work and some of the theoretical work has been done jointly with Anna Gajdova, David Lindner, Lukas Finnveden, and Rajashree Agrawal as part of the third AI Safety Camp. We are grateful to Ryan Carey and Geoffrey Irving for the advice regarding this project. The remainder of the theoretical part relates to my stay at FHI, and I would like to thank the above people, Owain Evans, Michael Dennis, Ethan Perez, Stuart Armstrong, and Max Daniel for comments/discussions.
Debate is a recent proposal for AI alignment, which naturally incorporates elicitation of human preferences and has the potential to offload the costly search for flaws in an AI’s suggestions onto the AI. After briefly recalling the intuition behind debate, we list the main open problems surrounding it and summarize how the existing work on debate addresses them. Afterward, we describe, and distinguish between, Debate games and their different applications in more detail. We also formalize what it means for a debate to be truth-promoting. Finally, we present results of our experiments on Debate games and Training via Debate on MNIST and fashion MNIST.
Debate games and why they are useful
Consider an answer to some question --- for example, "Where should I go for a vacation?" and "Alaska". Rather than directly verifying whether is an accurate answer to , it might be easier to first decompose into lower-level components (How far/expensive is it? Do they have nice beaches? What is the average temperature? What language do they speak?). Moreover, it isn't completely clear what to do even if we know the relevant facts --- indeed, how does Alaska's cold weather translate to a preference for Alaska from 0 to 10? And how does this preference compare to English being spoken in Alaska? As an alternative, we can hold a debate between two competing answers and ="Bali" to . This allows strategic debaters to focus on the most relevant features of the problem (perhaps the language isn't important), and replace the possibly-difficult direct evaluation by often-simpler comparison of two options (whatever their position on a 0-10 scale, Bali's beaches are clearly better than Alaska's).
Importantly for AI-alignment, this approach also naturally incorporates elicitation of human feedback. Recently, the paper AI Safety via Debate [1] proposed training agents via self-play on a zero-sum debate game. Given a question or proposed action, two agents take turns making short statements up to a limit, then a human judges which of the agents gave the most true, useful information.
Unlike [1] we explicitly distinguish between debating over which of the answers is better (Debate game) and coming up with answers for which to argue. This is useful since the two tasks often require somewhat different skills, and they might be performed by different agents. Moreover, this distinction highlights the fact that Debate games have several other uses apart from “training via debate”: below, we also describe how to use Debate games for “answer verification” and “incentivizing an AI to give a useful answer”.
Terminology remark: To settle on precise terminology, we use "question", "answers", and "arguments" to refer to the topic of the debate, the initial claims made by the two debaters, and the subsequent statements made during the debate. However, the usefulness of debates is by no means restricted to Oracle AIs since we could also consider questions of the form ="Which policy would you adopt to perform task ?".
Open problems around AI Safety Debate
We now list the main high-level open problems around AIS debate. For further open questions and suggestions for future work, see the original Debate paper. In particular, we do not discuss the issues related to holding the debate in natural-language or the possibility of hacking the human judge while debating.
(H) How exactly does debate look like? To be able to apply debate in the first place, we need to understand -- in enough detail to make the ideas implementable -- (i) what “holding a Debate game around ” means and (ii) how to use this Debate game for getting useful answers to .
(TW) Does truth win? Crucially, the optimal strategy in a Debate game corresponding to , , and consists of making the most convincing arguments --- not the truthful ones. Similarly, the optimal way of selecting which answer to argue for (described in more detail in a later section) is to choose the most convincing answer --- not the correct one. For debate to be useful, we need to understand the conditions under which persuasiveness coincides with truthfulness. Indeed, as we can see at the example of political debate on the one hand and mathematical proofs on the other, different “debate settings” can greatly influence whether debate is truth-promoting or not.
(C) Competitiveness: Is the debate approach comparably efficient with alternative ways of obtaining answers to ? (If not, then the economic incentives might prevent it from being adopted.)
State of the art: The original Debate paper gave some examples of (H)(i) and presented an initial ML experiment to address (TW), showing that an MNIST debate (described in the paper) is reasonably truth-promoting. Regarding (TW), it also showed that a certain idealized version of debate solves problems in the PSPACE class. As we point out later, an analogy can be made between “training via debate” and the AlphaZero algorithm. This gives some evidence that the answer to (C) might be positive.
Our work: As a part of the third AI Safety camp, we sought to better understand (H) and (TW). The present document summarizes our theoretical progress in (H). Regarding (TW), we have replicated the MNIST experiment above. We have then extended the Debate game to fashion MNIST and investigated the impact of several different debate protocols. We have also implemented a prototype architecture that uses the Debate game for training. We view this prototype as a part of (H)(ii) and a prerequisite to the investigation of (C). The main results of these experiments are presented below. Further questions we wish to investigate are listed in this google doc.
Technical description of Debate games
As a way of getting closer to answering the first part of (H), we can think of a debate game as having the following ingredients:
- Question: A high-level and/or difficult-to-answer question in whose answer we are interested.
- Answers: Candidates and for a correct answer to .
- Low-level components: Facts about , , and (e.g., the distance to Bali, temperature in Alaska in July, visa rules in Bali, ...).
- Decomposition: The rules governing how the low-level components of aggregate into which of the two answers is better (e.g., the temperature only matters if we can actually get to the place, the expenses are additive, ...).
- Debate protocol: The syntax of arguments the debaters can make, rules governing which arguments are allowed in which part of the debate, a way of deciding when the debate ends, and possibly some other parts.
- Judge: A way of: (a) expressing preferences about low-level components ("I like warm weather more than a blizzard."), (b) verifying claims about them (googling for weather Alaska, having a vague impression that Alaska is closer to Europe than Bali) and about the decomposition ("If Bali is warmer and I can get there, then I like it more."), and (c) observing adherence to the debate protocol.
Together, these ingredients combine into a Debate game, which can be played by agents possessing varying levels of knowledge and debate skill:
i. Agents state their answers to the judge (independently of each other).
ii. The agents take turns making arguments to the judge. These can relate to (a) , (b) the pair , (c) all arguments made so far, or any combination of (a)-(c).
- Which arguments are legal depends on the decomposition and the debate protocol.
- Which arguments actually end up being made depends on the agents and their debating skill and knowledge.
iii. Once arguments get sufficiently low-level, they are used as in input for the judge, whose output then determines the winner and the corresponding utilities , .
Remarks:
- While the ingredients above seem fruitful for thinking about Debate games, the line between low-level components, decomposition, and debate protocol might often be blurry.
- The judge might be suboptimal or biased in many ways (e.g., being mistaken about their preferences, having a chance of making errors verifying facts or decomposition, not having access to the correct information in the first place, being prone to deception).
- Debate games make sense even when there is no human-preference aspect; indeed, the self-play performed by AlphaZero's training procedure is a prime example of this ([1]).
- In human debates, it is expected that neither of the debaters has a full picture, and it is, therefore, acceptable to make a false sub-claim that the debater later retracts. However, we typically hold the debating AIs to a higher standard, meaning that as soon as any of the sub-claims made in the debate is proven wrong, the agent who made that claim loses the debate.
Examples
- Consider the question “How many bridges do you cross when taking the Trans-Siberian Railway?”. To get to a low-level question “Is there a bridge between points A and A + 100m ?”, answerable by a google-maps “judge”, we can use the decomposition rule “bridges in [A,C] = bridges in [A,B) + bridges in [B,C]” One viable debate protocol is that one agent proposes the answer “There are bridges between 0 km and 9 258 km”. If the other agent opposes the answer, the debate proceeds recursively by the proponent claiming that “There are bridges between 0 km and km and between km and 9258 km.” and the opponent choosing whether to dispute the first or the second part.
- The debate protocol can be very informal, such as in real-life debates. However, it can also be very formal, such as when two players (implicitly) announce “I am better at chess than you!”, and then play a match to prove their points.
- Debates can vary a lot in how truth-promoting they are --- from political debates on one side of the spectrum to mathematical proofs (and their verification) on the other.
Applications of Debate games
To partially address the second part of (H), we list three applications of Debate games that would --- assuming all the details can be fleshed out --- all be relevant to AI alignment.
A) Answer verification
Suppose we have an answer to some question , but we don't know whether is trustworthy or not ( could be our best guess at , or something suggested by a black-box AI). To increase our confidence in the answer, we call in two debate AIs, and have one argue for " is a correct answer to " and the other for " is a wrong answer to ". Alternatively, we generate a lot of competing answers , and have debates over "Which better answers , or ?". If loses any of the debates, we throw it away (while learning what was wrong with it). Stuart Armstrong’s Devil’s advocate AI falls under (A).
B) Training via Debate (debate as a training signal)
Let be a class of questions. Suppose that you cannot directly evaluate how good an answer A is to but for any alternative you can compare whether is better or worse than by zooming in on some details of and . We then train a question-answering system for using some form of active learning, where self-play debates between promising answers are used as a training signal. AlphaZero is an instance of (B).
C) Incentivizing an AI to give a useful answer
Suppose we have two strong AIs capable of answering some question (e.g., Oracles). We can incentivize useful answers to by rewarding the AI whose answer wins the debate over "Which is a better answer to , or ?" (the debaters might, or might not, be the original two AIs).[1] I am not aware of an existing instance of (C).[2]
We now give several examples and a more detailed description of the Debate game and its ingredients. We then briefly recap the progress made so far, highlight related open questions, and give a non-technical summary of the experimental results obtained at the third AI Safety Camp.
Truth-promotion as the key desired property of Debate games
We now give a more precise game-theoretical definition of truth-promotion for (TW).
Consider a space of possible answers to a question . For fixed answers and debating policies , , the expected outcome of the Debate game is some . For simplicity, assume that only has one correct answer . As a first approximation of debate's usefulness, we can define the truth-win probability as the chance that to wins () against a randomly chosen . This definition is somewhat vague and sensitive to the choice of , but it has one more important problem: even with there might be an alternative incorrect answer that wins more debates than , and conversely, even with it might be the case that all other answers win even fewer debates than .
Rather than depending on win-probability in the above sense, an "optimal" choice of an answer to then corresponds to finding some Nash equilibrium of the (zero-sum) matrix game with payoff matrix and selecting . We say that debate about is truth-promoting if the only Nash equilibrium of is the pure strategy under which both players pick .[3] More generally, we define the truth-promotion likelihood as the probability of picking the correct answer under a (uniformly) randomly selected Nash equilibrium strategy.[4] This will be 0 or 1 for questions with a single, pure, equilibrium, but can be any number in between for questions with multiple equilibria or mixed equilibria.
Overall, we conjecture that most (reasonable) applications of debate will be successful if and only if the corresponding truth-promotion likelihoods are high.
Experimental results
This section presents the experimental results of our AISC3 project. The implementation can be found here. We assume that the reader is familiar with the MNIST debate experiment from [1]. Since the details of that experiment are somewhat specific, we highly recommend reading Section 3.1 of [1] before interpreting the results presented below.
Debate games
Recall that [1] considers Debate games around the question “Which digit is shown on this MNIST image?”, with the judge being a neural network classifier that can only see 4 (or 6) pixels of the image, and debate protocol “agents take turns revealing non-black pixels of the digit, until 4 (6) pixels have been revealed”. The debaters select their actions using a Monte Carlo tree search (MCTS) algorithm.
As the first step in our empirical investigation, we reimplemented this experiment, investigated how the results change if we vary the length of debates and the strength of the debaters, and extended the results to the fashion MNIST dataset. The table below shows that our results closely resemble[5] those of [1].
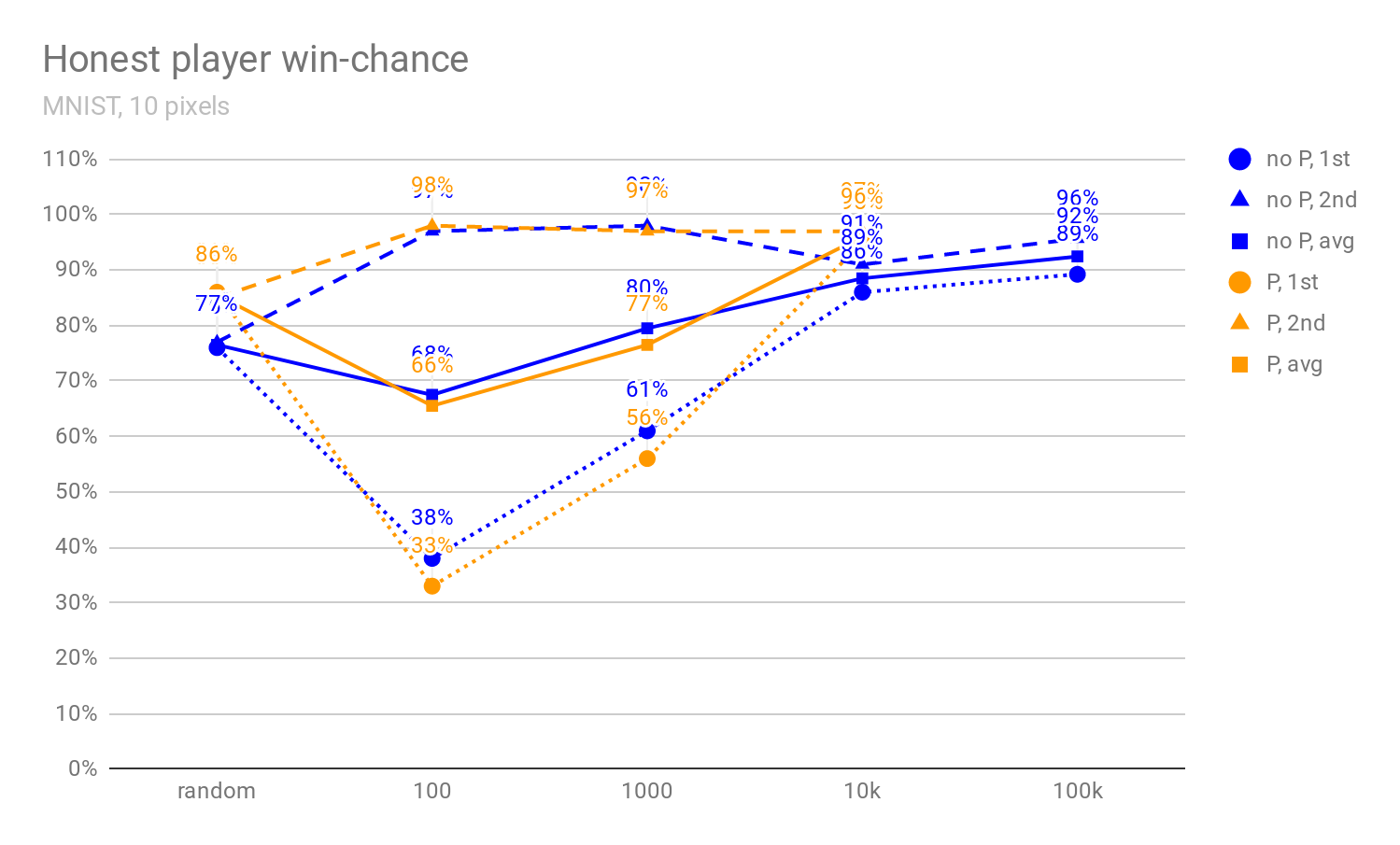
In Figures 1, 2, and 3 below, we can see how the honest player’s win-chance (defined in more detail in [1]) increases when more pixels are shown (4, 6, or 10), and how it develops as the debaters get stronger (i.e., as MCTS uses more rollouts). In particular, we see that there is initially a massive advantage in being the second player, and this advantage mostly disappears once the debaters are strong enough. This implies that the ability of the second player to react to the actions of the first player isn’t decisive in the MNIST debate; rather, we conjecture that the main reason for this “last-mover advantage” is that it’s easier for MCTS algorithm to look fewer moves ahead.
Figures 1 to 3: The percentage of images for which the honest player wins the debate against a non-precommitted opponent (no P), resp. all debates against a precommitted opponent (P) (see [1]).
The x-axis denotes the number of MCTS rollouts per decision; 0-rollout MCTS chooses actions randomly.
The "avg" graph depicts the average of win-chance when the honest player goes first and second.
The 0, 100, 1000, 10k, and 100k-rollout statistics are evaluated on 10k, 4k, 400, 100, and 100 images respectively (possibly explaining the drop between 10k and 100k win-rate).
Note that randomly selecting an answer would lead to 10% accuracy (and not, e.g., 50%).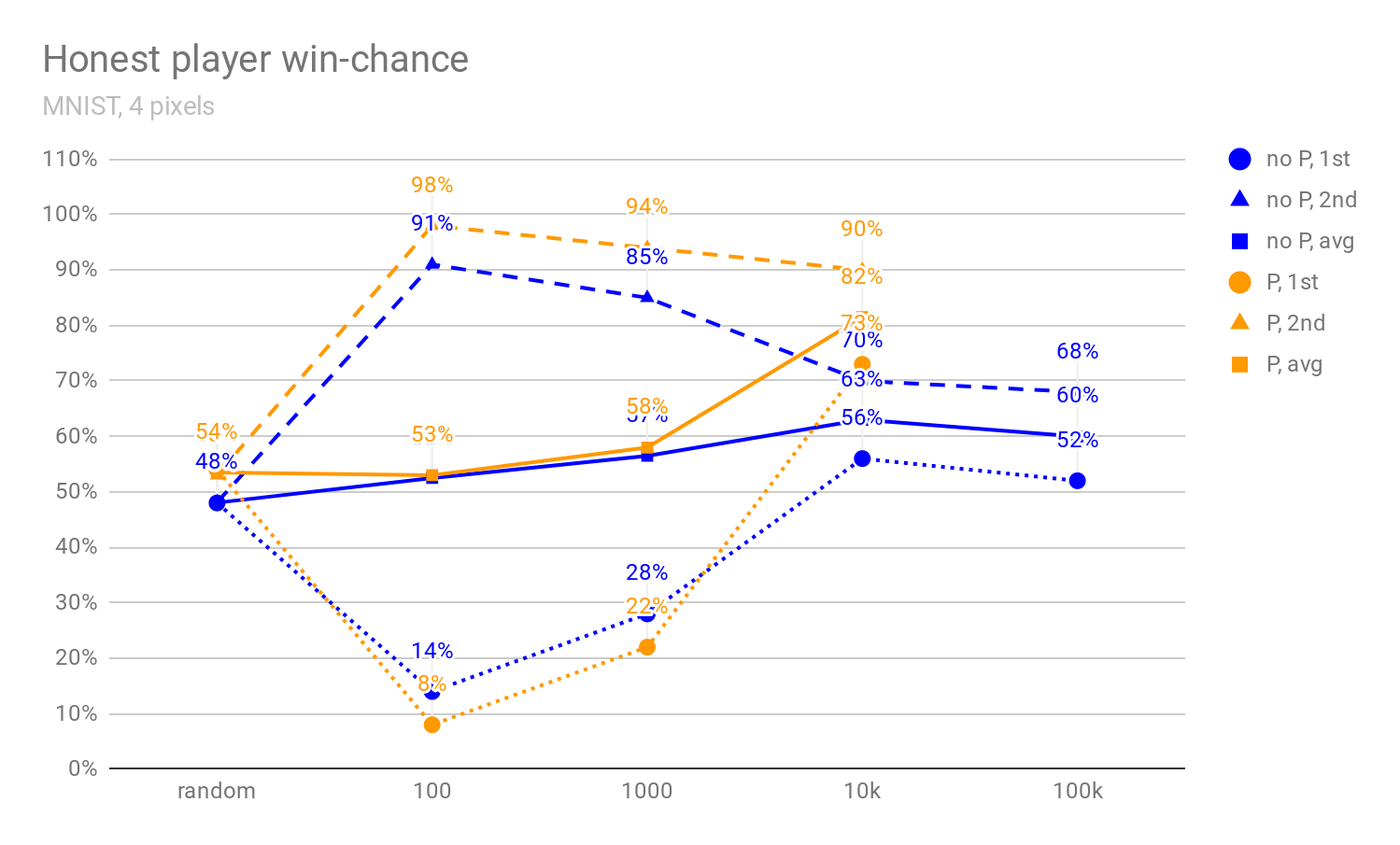
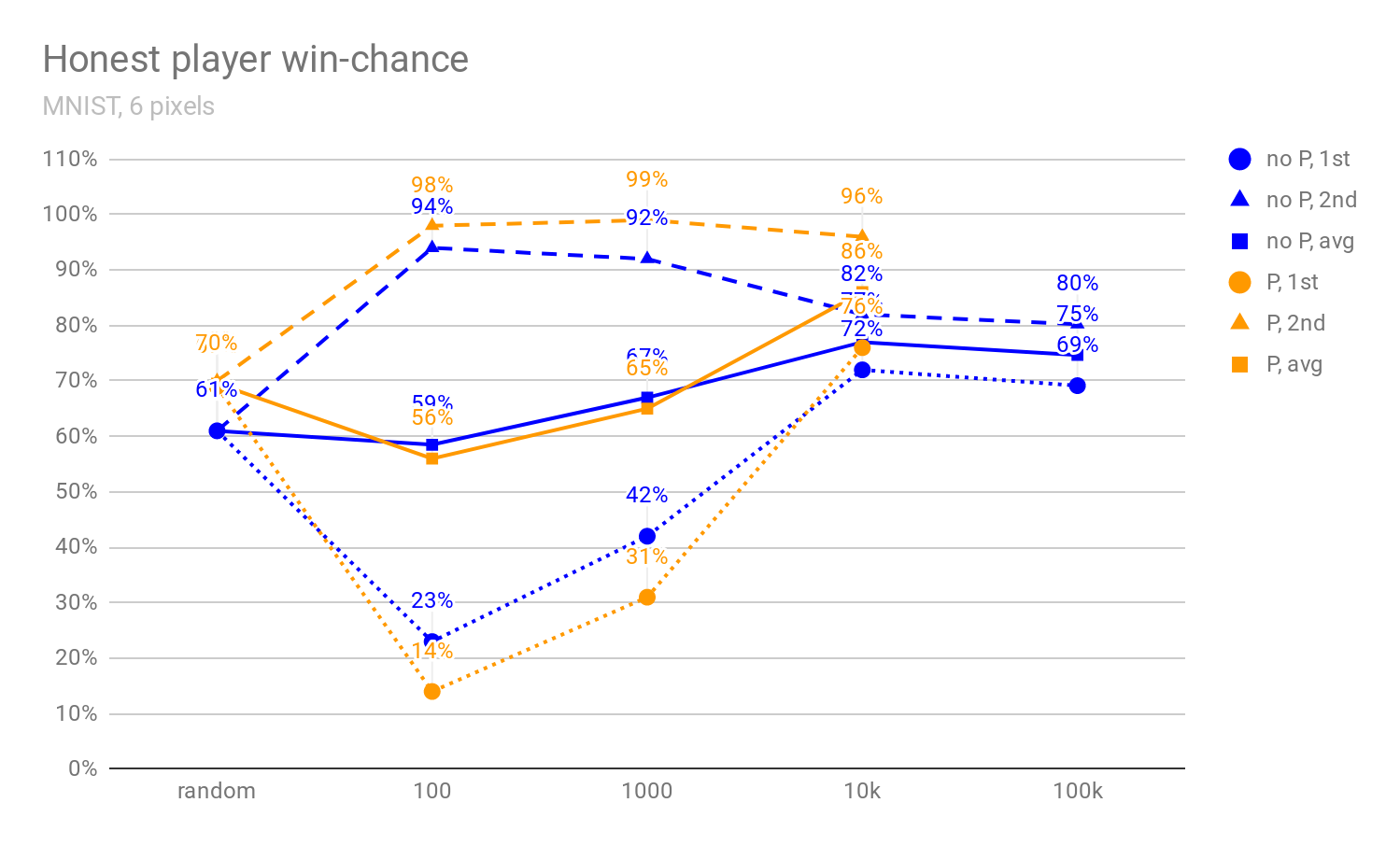
In all scenarios, the honest-player win rates are somewhat lower for fashion MNIST (Figures 4, 5, and 6) --- we believe this is because the fashion MNIST game is more difficult than the standard MNIST, mostly because there are more non-black pixels, which makes the branching factor of the game tree roughly an order of magnitude higher.
Figures 4 to 6: Fashion MNIST variants of Figures 1, 2, and 3.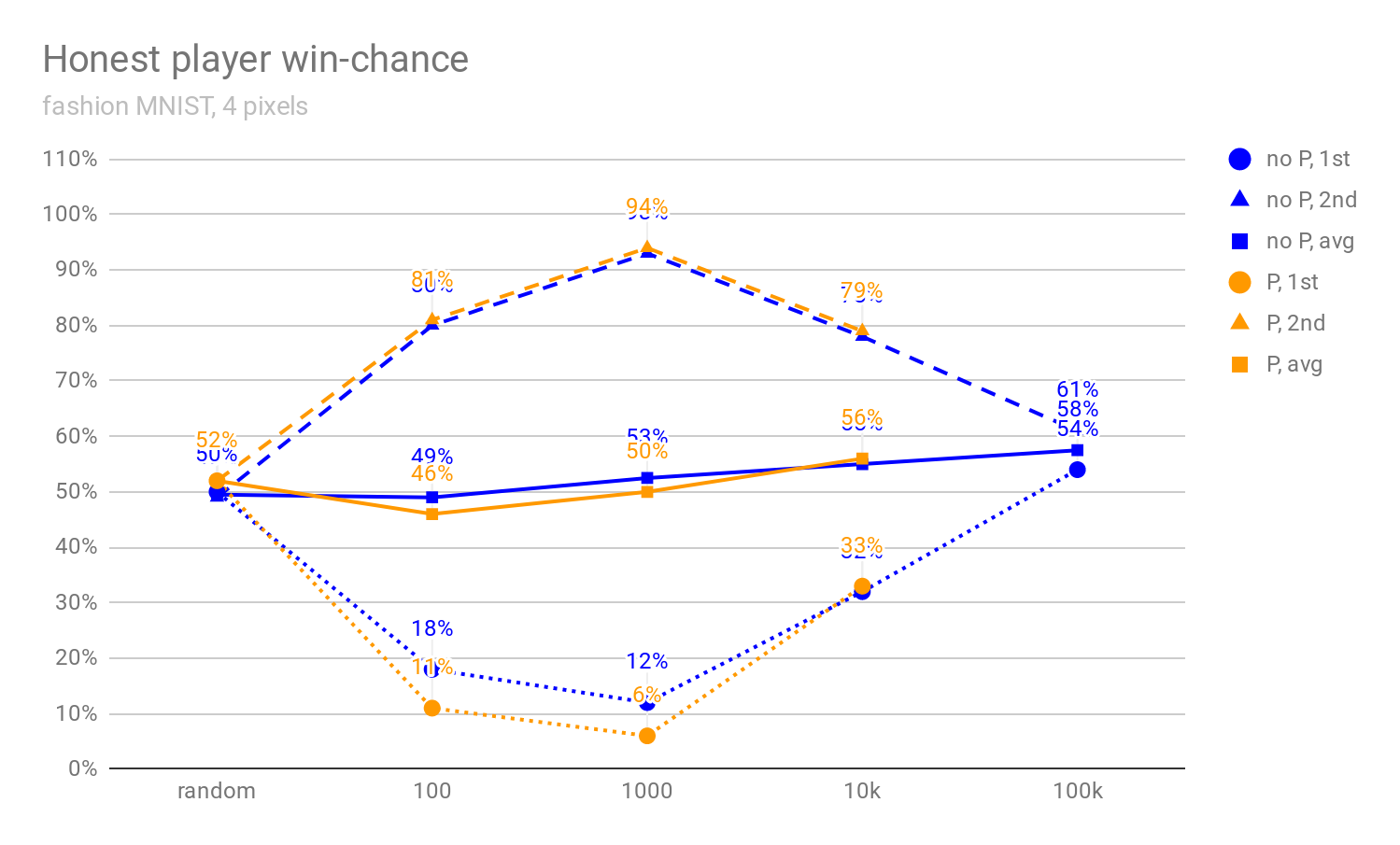
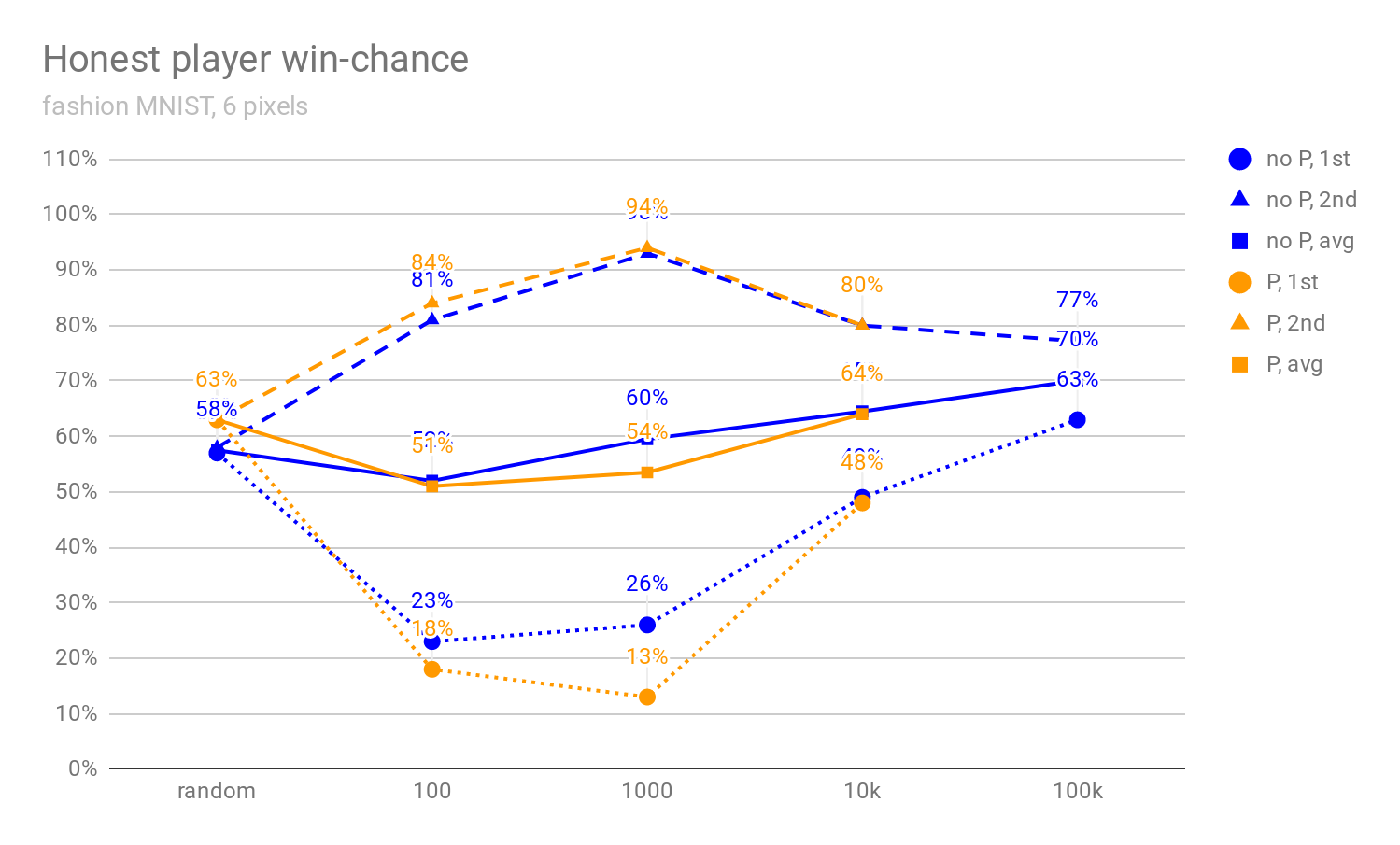
While the above measurements do give some indication of how often is the MNIST debate truth-promoting, it is not true that the average of honest player’s win chances (depending on whether they go first or second) would be an accurate estimate of (or even equal to) the truth-promotion likelihood. The reason for using the win-chances as defined in [1] was that it allows for a comparison of results, but also that a rigorous measurement of requires more computational resources (at least without further theoretical insights). As future work, we plan to measure more precisely and analyze how often is there a single best answer (when the starting player is selected randomly[6]).
Training via Debate
Figure 7: A simple architecture for Training via Debate.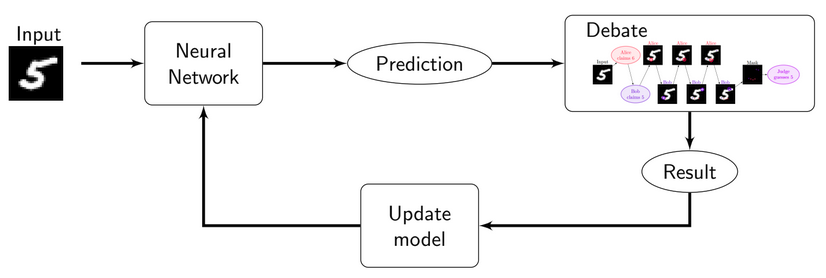
As our main practical contribution, we implemented a prototype pipeline (above) for training a (full) MNIST classifier when one only has access to Debate games, but not to the true labels. The main idea to use the neural network to predict a label for an image, run a debate against the non-precommitted opponent[7] (using the terminology of [1]), and update the neural network weights towards the label only if it won the debate. In the graph below, we see that the training procedure is stable, and achieves an accuracy that is even significantly higher than the honest player's win-chance in the corresponding debates (this is probably due to some of the errors canceling out during the training). While this training only used the rather weak 100-rollout MCTS debaters[8], it nonetheless demonstrates the viability of Training via Debate in this setting.
Figure 8: Accuracy of an MNIST classifier trained via debates that used a 6-pixel sparse classifier as a judge (without access to the true labels) and 100-rollout MCTS debaters. Each line depicts one run of training.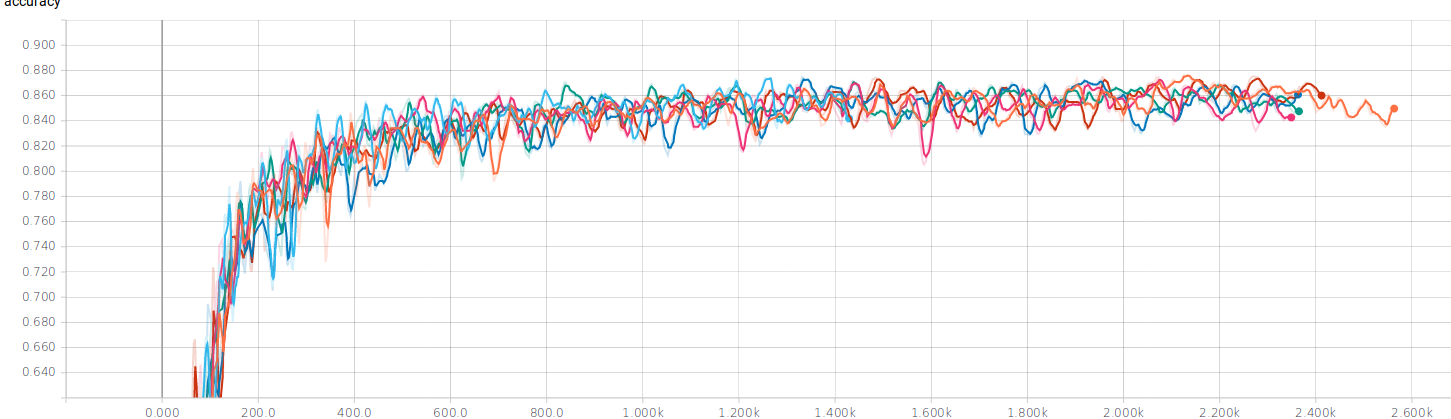
[1] Irving, Geoffrey, Paul Christiano, and Dario Amodei. "AI safety via debate." arXiv preprint arXiv:1805.00899 (2018).
Since the AIs are assumed to maximize the reward, and they know how the process works in advance, we hope that both and will be good answers to Q (possibly even having ). The debate and the consequent rewards thus only serve as an incentive for the AIs, and we should be able to adopt either of the answers without knowing the result. ↩︎
Arguably, (B) and (C) are similar in spirit, and in particular, an agent might implement (B) to perform well in (C). The main differences are that (i) a human commissions the debate in (C) while an AI does so in (B), (ii) answers in (C) are selected strategically whereas those in (B) aim to maximize information value, and (iii) only one question gets answered in (C). Moreover, (iv) the debates in (B) are likely to be judged automatically while those in (C) are judged by an actual human. ↩︎
If the only Nash equilibrium is select the true answer 100% of the time, all incorrect answers are "unstable" in the sense that there exists some other answer which will expose them (i.e., win the Debate game against them). However, this answer doesn't necessarily have to be the true one --- truth might tie against them. However, we can also require a stronger property where the true answer wins the Debate game against every other answer. (_h/t Max Daniel) ↩︎
Since Nash equilibria in two-player zero-sum games form a simplex, we have for the center of the NE simplex. ↩︎
Note that we used the standard version (rather than PUCB as in [1]) of the Monte Carlo tree search algorithm (which is furthermore inherently non-deterministic). Also, due to computational limitations, we only used 100 images to evaluate our results, instead of 10 000 used in [1]. This probably explains the differences in obtained win-rates. ↩︎
We cannot hope to decide whether the honest debater goes first or second since in practical applications of debate, we would not know which debater is which. ↩︎
Running the non-precommitted debate isn't the only way of implementing Training via Debate --- we chose this approach to simplify implementation and reduce computation time. ↩︎
Due to computational restrictions, we only ran Training via Debate using the results of debates between 100-rollout-MCTS agents. As one can guess from looking at Figure 2, this leads to similar performance as training from random debates. However, more computation and an optimized implementation should allow for training with much stronger debaters and (according to Figure 2) lead to significantly better accuracy. ↩︎