TL;DR: In this post, I distinguish between two related concepts in neural network interpretability: polysemanticity and superposition. Neuron polysemanticity is the observed phenomena that many neurons seem to fire (have large, positive activations) on multiple unrelated concepts. Superposition is a specific explanation for neuron (or attention head) polysemanticity, where a neural network represents more sparse features than there are neurons (or number of/dimension of attention heads) in near-orthogonal directions. I provide three ways neurons/attention heads can be polysemantic without superposition: non-neuron aligned orthogonal features, non-linear feature representations, and compositional representation without features. I conclude by listing a few reasons why it might be important to distinguish the two concepts.

Epistemic status: I wrote this “quickly” in about 12 hours, as otherwise it wouldn’t have come out at all. Think of it as a (failed) experiment in writing brief and unpolished research notes, along the lines of GDM or Anthropic Interp Updates.

Introduction

Meaningfully interpreting neural networks involves decomposing them into smaller interpretable components. For example, we might hope to look at each neuron or attention head, explain what that component is doing, and then compose our understanding of individual components into a mechanistic understanding of the model’s behavior as a whole.

It would be very convenient if the natural subunits of neural networks – neurons and attention heads – are monosemantic – that is, each component corresponds to “a single concept”. Unfortunately, by default, both neurons and attention heads seem to be polysemantic: many of them seemingly correspond to multiple unrelated concepts. For example, out of 307k neurons in GPT-2, GPT-4 was able to generate short explanations that captured over >50% variance for only 5203 neurons, and a quick glance at OpenAI microscope reveals many examples of neurons in vision models that fire on unrelated clusters such as “poetry” and “dice”.

One explanation for polysemanticity is the superposition hypothesis: polysemanticity occurs because models are (approximately) linearly representing more features^[1] than their activation space has dimensions (i.e. place features in superposition). Since there are more features than neurons, it immediately follows that some neurons must correspond to more than one feature.^[2] 

It’s worth noting that most written resources on superposition clearly distinguish between the two terms. For example, in the seminal Toy Model of Superposition,^[3] Elhage et al write:

Why are we interested in toy models? We believe they are useful proxies for studying the superposition we suspect might exist in real neural networks. But how can we know if they're actually a useful toy model? Our best validation is whether their predictions are consistent with empirical observations regarding polysemanticity.

(Source)

Similarly, Neel Nanda’s mech interp glossary explicitly notes that the two concepts are distinct:

Subtlety: Neuron superposition implies polysemanticity (since there are more features than neurons), but not the other way round. There could be an interpretable basis of features, just not the standard basis - this creates polysemanticity but not superposition.

(Source)

However, I’ve noticed empirically that many researchers and grantmakers identify the two concepts, which often causes communication issues or even confused research proposals. 

Consequently, this post tries to more clearly point at the distinction and explain why it might matter. I start by discussing the two terms in more detail, give a few examples of why you might have polysemanticity without superposition, and then conclude by explaining why distinguishing these concepts might matter.

A brief review of polysemanticity and superposition

Neuron polysemanticity

Neuron polysemanticity is the empirical phenomenon that neurons seem to correspond to multiple natural features.

The idea that neurons might be polysemantic predates modern deep learning – for example, the degree of polysemanticity of natural neurons is widely discussed in the neuroscience literature even in the 1960s, though empirical work assessing the degree of polysemanticity seems to start around the late 2000s. ML academics such as Geoffrey Hinton were talking about factors that might induce polysemanticity in artificial neural networks as early as the early 1980s.^[4] That being said, most of these discussions remained more conceptual or theoretical in nature.

Modern discussion of neuron polysemanticity descends instead from empirical observations made by looking inside neural networks.^[5] For example, Szegedy et al 2013 examines neurons in vision models, and find that individual neurons do not seem to be more interpretable than random linear combinations of neurons. In all of Nguyen et al 2016, Mu and Andreas 2020, and the Distill.pub Circuits Thread, the authors note that some neurons in vision models seem to fire on unrelated concepts. Geva et al 2020 found that the neurons they looked at in a small language model seemed to fire on 3.6 identifiable patterns on average. Gurnee et al 2023 studies the behavior of neurons using sparse linear probes on several models in the Pythia family and finds both that many neurons are polysemantic and that sparse combinations of these polysemantic neurons can allow concepts to be cleanly recovered. And as noted in the introduction, out of 307k neurons in GPT-2, GPT-4 was able to generate short explanations that captured over >50% variance for only 5203 neurons, a result that is echoed by other attempts to label neurons with simple concepts. I'd go so far as to say that every serious attempt at interpreting neurons in non-toy image or text models has found evidence of polysemantic neurons.
 

The reason neuron polysemanticity is interesting is that it’s one of the factors preventing us from mechanistically interpreting neural networks by examining each neuron in turn (on top of neurons just being completely uninterpretable, with no meaningful patterns at all in its activation). If a neuron corresponds to a simple concept, we might hope to just read off the algorithm a network implements by looking at what features of the input neurons correspond to, and then attributing behavior to circuits composed of these interpretable neurons. But if neurons don’t have short descriptions (for example if they seem to be best described by listing many seemingly unrelated concepts), it becomes a lot harder to compose them into meaningful circuits. Instead, we need to first transform the activations of the neural network into a more interpretable form.^[6] 

Superposition

Superposition occurs when a neural network linearly represents more features than its activations have dimensions.^[7] The superposition hypothesis claims that polysemanticity occurs in neural networks because of this form of superposition.

There are two important subclaims that distinguish superposition from other explanations of polysemanticity. In the superposition hypothesis, features both 1) correspond to directions (and are approximately linearly represented) and 2) are more plentiful than activation dimensions.

The true environment could have 10 million “features”,^[8] but the model with width 10,000 may not care and represent only 10 of them instead of placing a much larger number into superposition. In the case where the model represents only 10 features, you might hope to find a linear transformation that recovers these features from the model’s activations. In contrast, when the network represents 1 million of the 10 million features, no orthogonal transformation exists that recovers all the “features” encoded in the MLP activations (respectively, attention heads) because there are more features than the model has dimensions.

The standard reference for discussions of superposition is Anthropic’s Toy Model of Superposition, which mainly considers superposition in the toy cases of storing disentangled sparse features in a lower dimensional representation, such that the features can then be ReLU-linearly read off – that is, you can reconstruct the (positive magnitude of) features by a linear map followed by a ReLU – and secondarily the case of using a single fully connected layer with fewer neurons than inputs to compute the absolute value of features. Recently, Vaintrob, Mendel, and Hänni 2024 proposed alternative models of computation in superposition based on small boolean operations that MLPs and attention heads can implement.

There are two key factors that coincide to explain why superposition happens inside of neural networks. Different explanations or models emphasize one reason or the other, but all models I’m aware of assume some form of both:

1. High dimensional space contains many near orthogonal directions. In general, there are $2^{\Theta \left(d{\epsilon }^2\right)}$ (that is, exponentially many) unit vectors in ${\text{R}}^d$ with inner product at most epsilon.^[9] This means that you can have many features that have a small inner product, and thus don’t interfere much with each other. In fact, these vectors are easy to construct – it generally suffices just to take random corners of a centered d-dimensional hypercube. 
2. “Features” are sparse in that only few are active at a time. Even if every other feature is represented by a direction that only interferes with any particular feature a tiny amount, if enough of them are active at once, then the interference will still be large and thus incentivize the model representing fewer features. However, if only a few are active, then the expected interference will be small, such that the benefit of representing more features outweighs the interference between features. In fact, you can get superposition in as few as two dimensions with enough sparsity (if you allow large negative interference to round off to zero)!^[10] As a result, models of superposition generally assume that features are sparse.^[11]

Polysemanticity without superposition

In order to better distinguish the two (and also justify the distinction), here are some alternative reasons why we might observe polysemanticity even in the absence of superposition.

Example 1: non–neuron aligned orthogonal features

There’s a perspective under which polysemanticity is completely unsurprising – after all, there are many possible ways to structure the computation of a neural network; why would each neuron correspond to a unique feature anyways?

Here, the main response is that neurons have element-wise activation functions, which impose a privileged basis on activation space. But despite this incentive to align representations with individual neurons, there are still reasons why individual neurons may not correspond to seemingly natural features, even if the MLP activations are linearly representing fewer features than neurons.

1. Neural networks may implement low-loss but suboptimal solutions: Optimal networks may have particular properties that networks that Adam finds in reasonable time starting from standard network initializations do not.^[12] Even for problems where there's a single, clean, zero-loss global minima, there are generally low-loss saddle points featuring messy algorithms that incidentally mix together unrelated features.^[13]  I think that this is one of the most likely alternatives to superposition for explaining actual neuron polysemanticity. 
   
   Feature sparsity exacerbates this problem: when features are sparse (as in models of superposition), interference between features is rare. So even when the minimum loss solution has basis-aligned features, the incentive toward aligning the features to be correct on the cases where both features are present will be at a much lower expected scale than the incentive of getting the problem correct in cases where only a single feature is present, and may be swamped by other considerations such as explicit regularization or by gradient noise.^[14] 
2. Correlated features may be jointly represented: If features x and y in the environment have a strong correlation (either positive or negative), then the model may use a single neuron to represent a weighted combination of x and y instead of using two neurons to represent x and y independently.^[15] It's often the case that datasets contain many correlations that are hard for humans to notice. For example, image datasets can contain camera or post-processing artifacts and many seemingly unimportant features of pretraining datsets are helpful for next-token prediction. It seems possible to me that many seemingly unrelated concepts actually have meaningful correlation on even the true data distribution. 
   
   That being said, this does not explain the more obvious cases of polysemanticity that we seem to find in language models, where the features the neurons activate strongly on features that are almost certainly completely unrelated.
3. The computation may require mixing together “natural” features in each neuron: The main reason we think any particular neuron is polysemantic is that the features do not seem natural to interpretability researchers. But it might genuinely be the case that the optimal solution does not have neurons that are aligned with “natural” features!
   
   For example, the “natural” way to approximate x * y, for independent x and y, with a single layer ReLU MLP, is to learn piecewise linear approximations of $(x+y{)}^2/4$ and $(x-y{)}^2/4$, and then taking their difference.^[16] A naive interpretability researcher looking at such a network by examining how individual neurons behave on a handcrafted dataset (e.g. with contrast pairs where only one feature varies at a time) may wonder why neuron #5 fires on examples where x or y are both large.^[17] No superposition happens in this case – the problem is exactly two dimensional – and yet the neurons appear polysemantic.
   
   Arguably, this is a matter of perspective; one might argue that x+y and x-y are the natural features, and we’re being confused by thinking about what each neuron is doing by looking at salient properties of the input.^[18] But I think this explains a nonzero fraction of seemingly polysemantic neurons, even if (as with the previous example) this reason does not explain the more clear cases of polysemanticity inside of language models.

The fact that there are fewer features than neurons makes this case meaningfully distinct from superposition, because there exists an orthogonal transformation mapping activations onto a basis made of interpretable features, while in the superposition case no such transformation can exist.

Example 2: non-linear feature representations

Neural networks are not linear functions, and so can make use of non-linear feature representations.

For example, one-layer transformers can use non-linear representations and thus cannot be understood as a linear combination of skip tri-gram features due to the softmax allowing for inhibition. In Anthropic’s January 2024 update, they find empirically that forcing activations of a one-layer transformer to be sparse can lead to the network using non-linear representations via a similar mechanism. Outside of one-layer transformers, Conjecture’s Polytope Lens paper finds that scaling the activations of a single layer of InceptionV1 causes semantic changes later in the network.^[19] 

That being said, while I’d be surprised if neural networks used no non-linear feature representations, there’s a lot of evidence that neural networks represent a lot of information linearly. In casual conversation, I primarily point to the success of techniques such as linear probing or activation steering as evidence. It’s plausible that even if neural networks can and do use some non-linear feature representations, the vast majority of their behavior can be explained without referencing these non-linear features.

Example 3: compositional representation without “features”

More pathologically, neural networks have weights that allow for basically hash-map style memorization. For example, many of the constructions lower bounding the representation power of neural networks of a given size tend to involve “bit-extraction” constructions that use relus to construct interval functions that extract the appropriate bits of the binary representation of either the weights or the input.^[20] These approaches involve no meaningful feature representations at all, except insofar as it’s reasonable to use the exponentially many unique combinations of bits as your features.

The specific constructions in the literature are probably way too pathological to be produced by neural network training (for example, they often require faithfully representing exponentially large or small weights, in the dimension of the input, while any practical float representation simply lacks the precision required to represent these numbers). But it’s nonetheless conceptually possible that neural networks can represent something that’s better described as a dense binary representation of the input and not in terms of a reasonable number of linearly independent features, especially in cases where the neural network is trying to memorize large quantities of uniformly distributed data.^[21]

Conclusion: why does this distinction matter?

There’s a sense in which this post is basically making a semantic argument as opposed to a scientific one. After all, I don’t have a concrete demonstration of non-superposition polysemanticity in real models, or even a clear grasp of what such a demonstration may involve. I also think that superposition probably causes a substantial fraction of the polysemanticity we observe in practice.

But in general, it’s important to keep empirical observations distinct from hypotheses explaining the observations. As interpretability is a new, arguably pre-paradigmatic field, clearly distinguishing between empirically observed phenomena – such as polysemanticity – and leading hypotheses for why these phenomena occur – such as superposition – is even more important for both interpretability researchers who want to do and for grantmakers looking to fund impactful non-applied research.

In the specific case of polysemanticity and superposition, I think there are three main reasons:

Our current model of superposition may not fully explain neuron polysemanticity, so we should keep other hypotheses in mind

Polysemanticity may happen for other reasons, and we want to be able to notice that and talk about it.

For example, it seems conceptually possible that discussions of this kind are using the wrong notion of “feature".^[22] As noted previously, the form of sparsity used in most models of superposition implies a non-trivial restriction on what “features” can be. (It’s possible that a more detailed non-trivial model of superposition featuring non-uniform sparsity would fix this.^[23]) Assuming that polysemanticity and superposition are the same phenomenon means that it’s a lot harder to explore alternative definitions of “feature”.

Perhaps more importantly, our current models of superposition may be incorrect. The high dimensional geometry claim superposition depends on is that while there are only $d$ directions with dot product exactly zero (and $2d$ directions in $R^d$ with pairwise dot product $\le 0$), there are $O\left(2^{d{\epsilon }^2}\right)$ directions with dot production $\le \epsilon$. Presumably real networks learn to ignore sufficiently small interference entirely. But in Anthropic's Toy Model of Superposition, the network is penalized for any positive interference, suggesting that it may be importantly incorrect.^[24] 

In fact, after I first drafted this post, recent work came out from Google Deepmind that finds that SAEs that effectively round small positive interference to zero outperform vanilla SAEs that do not, suggesting that Anthropic’s Toy Model is probably incorrect in exactly this way to a degree that matters in practice. See the figure below, though note that this is not the interpretation given by the authors.

Attempts to “solve superposition” may actually only be solving easier cases of polysemanticity

In conversations with researchers, I sometimes encounter claims that solving superposition only requires this other concept from neuroscience or earlier AI/ML research (especially from junior researchers, though there are examples of very senior researchers also making the same error). But in almost every case, these ideas address polysemanticity that occurs from other reasons than superposition.

For example, disentangled representation learning is a large subfield of machine learning that aims to learn representations that disentangle features of the environment. But this line of work almost always assumes that there are a small number of important latent variables, generally much smaller than your model has dimensions (in fact, I’m not aware of any counter examples, but I’ve only done a shallow dive into the relevant literature). As a result, many of these approaches will only apply to the easier case where superposition is false and the features are represented as a non–neuron aligned basis, and not to the hard case where superposition occurs meaningfully in practice.

Clear definitions are important for clear communication and rigorous science

To be fully transparent, a lot of the motivation behind this post comes not from any backchaining from particular concrete negative outcomes, but instead a general sense of frustration about time wasted to conceptual confusions.

Poor communication caused in large part by confusing terminology is a real issue that’s wasted hours of my time as a grant-maker, and my own muddled thinking about concepts has wasted dozens if not hundreds of hours of my time as a researcher. It’s much harder to estimate the cost in good projects not funded or not even conceptualized due to similar confusions.

I’d like to have this happen less in the future, and my hope is that this post will help.

Acknowledgements

Thanks to Eleni Angelou, Erik Jenner, Jake Mendel, and Jason Gross for comments on this post, and to Dmitry Vaintrob for helpful discussions on models of superposition.

1. ^{^}

   I don't have a good definition of the word feature, and I'm not aware of any in the literature. I think the lack of a clear idea of what "good" or "natural" feature are lies behind a lot of conceptual problems and disagreements in mech interp. That being said, I don't think you can solve this problem by doing philosophy on it without running experiments or at least doing math. 

2. ^{^}

    For the sake of brevity, this post focuses primarily on superposition as an explanation for neuron polysemanticity, which is generally the type of polysemanticity that people study. Most of the claims straightforwardly apply to attention head superposition as well (both across attention heads and within a single attention head).

3. ^{^}

   After having read it in detail again for this post, I continue to think that Anthropic’s Toy Model of Superposition is an extremely well written piece, and would recommend at least reading the discussion and related work sections.

4. ^{^}

    See for example this 1981 paper from Hinton. 

5. ^{^}

    In fact, it’s pretty easy to replicate these results yourself without writing any code, by using e.g. OpenAI Microscope to look at neurons in vision models and Neel Nanda’s Neuroscope for neurons in text models.

6. ^{^}

   Polysemanticity is less of a concern for approaches that don’t aim to derive mechanistic understanding, e.g. linear probing does not care polysemanticity as long as the features you probe for are linearly represented.

7. ^{^}

   Jason Gross notes in private communication that originally, superposition (as used in quantum mechanics) did mean “features are not aligned with our observational basis” (in other words, superposition ~= polysemanticity):

   Superposition in quantum mechanics refers to the phenomenon that quantum systems can be in states which are not basis-aligned to physical observables, instead being linear combinations thereof.  For example, a particle might be in a superposition of being "here" and being "there", or in a superposition of 1/sqrt(2)(spin up + spin down), despite the fact that you can never observe a particle to be in two places at once, nor to have two spins at once.
   
   So if we stick to the physics origin, superposed representations should just be linear combinations of features, and should not require more features than there are dimensions.  (And it's not that far a leap to get to nonlinear representations, which just don't occur in physics but would probably still be called "superposition" if they did, because "superposition" originally just meant "a state where the position [or any other observable] is something other than anything we could ever directly observe it to be in")

   But “superposition” in the context of interpretability does mean something different and more specific than this general notion of superposition.

8. ^{^}

   Again, I'm intentionally leaving what a "feature" is vague here, because this is genuinely a point of disagreement amongst model internals researchers that this section is far too short to discuss in detail.

9. ^{^}

   Traditionally, this is shown by applying Johnson-Lindenstrauss to the origin + the standard basis in $R^m$ for m > d. You can also get this by a simple “surface area” argument – each unit vector “eliminates" a spherical cap on the unit hypersphere of exponentially decreasing measure in d (see this one-page paper for a concise mathematical argument), and so by greedily packing them you should get exponentially many near orthogonal unit vectors.

10. ^{^}

    Also, see any of the toy models in Anthropic’s TMS post, especially the 2 dimensional ones (like the one I included in this post). Note that while Anthropic’s TMS mentions both reasons, many of the toy models are very low-dimensional and mainly have superposition due to high sparsity + a slightly different definition of "linearly represented". 

11. ^{^}

     This is nontrivial (albeit fairly justifiable in my opinion) assumption: sparsity of this form rules out very compositional notions of feature; e.g. if books in your library can be fantasy, science fiction, and historical fiction, and then can each category can be English, Hindi, French, or Chinese, the corresponding sparse features would be of the form “is this book in English” or “is this the genre of this book fantasy” and not “language” or “fantasy”. As this example shows, these models imply by construction that there are many, many features in the world. Contrast this to latent variable-based definitions of features such as Natural Abstractions or representation learning, which tend to assume a small number of important “features” that are sparsely connected but almost always present.

12. ^{^}

     This is especially true if you didn’t initialize your network correctly, or used bad hyperparameters. Also, see the Shard Theory for a concrete example of how “optimized for X” may not imply “optimal for X”.

13. ^{^}

    I've checked this empirically on a few toy cases such as approximating the element-wise absolute value of sparse real-valued vectors or the pairwise and of boolean values, where the optimal solution given the number of neurons in the network is a basis aligned zero-loss solution. With many settings of hyperparameters (the main important ones that affect the results seem to be weight decay and sparsity), these one-layer MLPs consistently get stuck in low but non-zero loss solutions, even with large batch size and with different first-order optimizers. 
    
    Due to the small size of the networks, this specific result may be due to optimization difficulties. But even when the MLPs are made significantly wide, such that they consistently converge to zero loss, the networks do not seem to learn monosemantic solutions (and instead prefer zero-loss polysemantic ones). So I think there's some part of the explanation of this experimental result that probably involves learning dynamics and the inductive biases of (S)GD/Adam and how we initialize neural networks. 

14. ^{^}

     After drafting this post, I found this ICLR 2024 workshop paper that makes this case more strongly using a more thorough analysis of a slightly modified version of Anthropic’s Toy Model of Superposition, though I haven’t had time to read it in detail:

    [..] We show that polysemanticity can arise incidentally, even when there are ample neurons to represent all features in the data, a phenomenon we term \textit{incidental polysemanticity}. Using a combination of theory and experiments, we show that incidental polysemanticity can arise due to multiple reasons including regularization and neural noise; this incidental polysemanticity occurs because random initialization can, by chance alone, initially assign multiple features to the same neuron, and the training dynamics then strengthen such overlap.

15. ^{^}

     See e.g. this toy example in Anthropic’s Toy Model of Superposition.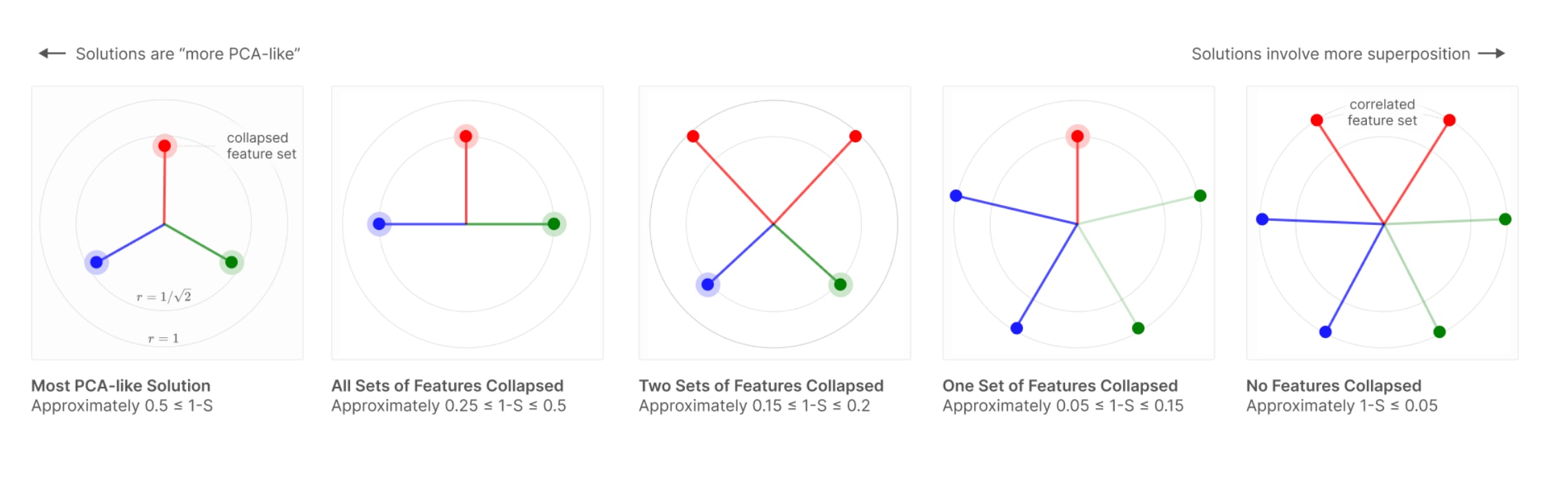 In this setting, the environment has 6 natural features by construction that occur in three correlated pairs. When features are sufficiently dense and correlated, the model learns to represent only 3 features, compared to the 4 signed directions in 2 dimensions. That being said, this example is more analogous to the residual stream than to MLP activations, and more importantly uses a different notion of "feature" than "linearly represented dimension". 

    I generally refer to these features as ReLU-linear and not linear. That is, you recover them by a linear transformation into a higher dimensional space, followed by a ReLU. This different definition of "feature" means the example is not perfectly analogous to the argument presented previously. (For example, interference between ReLU-linear features is zero as long as the inner product between features is at most zero, instead of being exactly equal to zero, so there are 2d such features in $R^d$: take any orthogonal basis and minus that basis.) 

16. ^{^}

     This uses the fact that $(x+y{)}^2-(x-y{)}^2=4xy$.

17. ^{^}

     This example isn’t completely artificial – it seems that this is part of the story for how the network in the modular addition work multiplies together the Fourier components of its inputs. Note that in this case, there is a low-dimensional natural interpretation that makes sense at a higher level (that the MLP layer linearly represents terms of the form cos(a)cos(b) and so forth), but looking at neurons one at a time is unlikely to be illuminating.

18. ^{^}

     I’m somewhat sympathetic to this perspective. For a more biting critique of interpretability along these lines, see Lucius Bushnaq’s “fat giraffe” example, though also see the discussion below that comment for counterarguments.

19. ^{^}

    That being said, note that Inception v1 uses Batch norm with fixed values during inference, so the results may not apply to modern transformers with pre-RMS norm.

20. ^{^}

     E.g. see the classic Bartlett et al 2019 for an example of extracting bits from the weights, and Lin and Jegelka 2018 which shows that 1 neuron residual networks are universal by extracting the appropriate bits from the input.

21. ^{^}

    Jake Mendel pointed out to me on a draft of the post that even if neural networks ended up learning this, none of our techniques would be able to cleanly distinguish this from other causes of polysemanticity. 

22. ^{^}

    Again, consider Lucius Bushnaq’s “fat giraffe” example as an argument that people are using the wrong notion of feature.

23. ^{^}

    For example, I think that you can keep most of the results in both Anthropic’s TMS and Vaintrob, Mendel, and Hänni 2024 if the feature sparsity is exponentially or power-law distributed with appropriate parameters, as opposed to uniform.

24. ^{^}

    There's another objection here, which goes along the lines of "why is large negative inference treated differently than positive interference?". Specifically, I'm not aware of any ironclad argument for why we should care about directions with pairwise dot product $\le \epsilon$ as opposed to directions with dot product $\in [-\epsilon ,\epsilon ]$. H/t Jake Mendel for making this point to me a while ago. 

    See Vaintrob, Mendel, and Hänni 2024 (of which he is a coauthor) for a toy model that does “round off” both small negative and small positive interference to zero. That being said, that model is probably also importantly incorrect, because the functions implemented by neural networks are almost certainly disanalogous to simple boolean circuits.