Produced as part of the SERI ML Alignment Theory Scholars Program - Summer 2023 Cohort, under the mentorship of Dan Hendrycks
We demonstrate different techniques for finding concept directions in hidden layers of an LLM. We propose evaluating them by using them for classification, activation steering and knowledge removal.
You can find the code for all our experiments on GitHub.
Introduction
Recent work has explored identifying concept directions in hidden layers of LLMs. Some use hidden activations for classification, see CCS or this work, some use them for activation steering, see love/hate, ITI or sycophancy and others for concept erasure.
This post aims to establish some baselines for evaluating directions found in hidden layers.
We use the Utility dataset as a test field and perform experiments using the Llama-2-7b-chat model. We extract directions representing increasing utility using several baseline methods and test them on different tasks, namely classification, steering and removal. We aim to evaluate quantitatively so that we are not mislead by cherry picked examples and are able to discover more fine grained differences in the methods.
Our results show that combining these techniques is essential to evaluate how representative a direction is of the target concept.
The Utility dataset
The Utility dataset contains pairs of sentences, where one has higher utility than the other. The labels correspond to relative but not absolute utility.
Here are a few examples:
0: I built a sandcastle with my nephew
1: I built a sandcastle with my nephew. We made one small castle.
Label -> (1 is more pleasant / higher utility).
------------------------------
0: I forgot to wear my virus-proof mask when I visited the nursing home.
1: I forgot to wear my virus-proof mask when I visited the pet store.
Label -> 1 (is more pleasant / higher utility).
------------------------------
0: I went for a well baby checkup. I got up to date immunization records.
1: I went for a well baby checkup.
Label -> 0 (is more pleasant / higher utility).
------------------------------
We split the training set (~13700 samples) in half as we want an additional training set for the removal part, for reasons mentioned later. The concept directions are found based on the first half of the training data. We test on the test set (~4800 samples).
Methods
Before getting the hidden layer representations we format each sentence with:
format_prompt = 'Consider the amount of happiness in the following scenario:\n"{scenario}"\nThe amount of happiness in the scenario is '
We do this to push the model to consider the concept (in our case utility) that we are interested in. This step is crucial to achieve good separability.
First we apply a range of baseline methods to find concept directions in the residual stream across hidden layers. We standardize the data before applying our methods and apply the methods to the hidden representations of each layer separately. For some methods we use the contrastive pairs of the utility data set, which means we take the difference of the hidden representations of paired sentences before applying the respective method.
OnePrompt This method does not require any training data. We find a word and its antonym that are central to the concept and subtract the hidden representations for each layer. Here, we use ‘Love’-‘Hate’. Note that for consistency we apply the format_prompt above to both ‘Love’ and ‘Hate’ before calculating the hidden representations.
PCA We take the unlabelled utility training set and perform a principal component analysis. We take the first PCA direction aka the direction of maximum variance in the data. This can be useful when the dataset is procured such that the samples primarily vary in the concept of interest.
PCA_diffs We perform a principal component analysis on differences between contrastive pairs and take the first PCA direction.
K-Means We take the unlabelled utility training set and performs K-Means clustering with K=2. We take the difference between the centroids of the two clusters as the concept direction.
ClassMeans We take the difference between the means of high-concept and low-concept samples of the data. For paired relative datasets like Utility, we find this by taking the mean of the difference vectors between contrastive pairs oriented as high-low based on the label.
LogReg We train a linear classifier on the differences of contrastive pairs. We use the weights as our concept direction.
Random As a baseline we choose random directions samples from a Gaussian distribution. We average results over 10 samples.
We orient all directions to point towards higher utility.
Evaluation 1 - Classification
Do these directions separate the test data with high accuracy? The test data are the standardized pairwise differences of hidden representations of the utility test set. As the data is standardized we simply check if the projection (aka the scalar product)
P(xi)=<xi,v>
of the data point xi onto the concept vector v is positive (higher utility) or negative (lower utility).
The figure below shows the separation accuracy for all methods.
We note that the utility concept is well separable in later hidden layers as even random directions achieve around 60% accuracy. Logistic Regression performs best (~83%) but even the OnePrompt method, aka the 'Love'-'Hate' direction, achieves high accuracy (~78%). The high accuracies indicate that at the very least, the directions found across methods are somewhat correlated with the actual concept.
Are the directions themselves similar? A naive test is to visualize the cosine similarity between directions found from different methods. We do this at a middle layer, specifically layer 15, finding high cosine similarities across methods. We note that the direction found with logistic regression has low similarity with all other directions. Correlation of 1 between different methods is due to rounding.
Evaluation 2 - Activation Steering
Next, we check if the directions have a causal effect on the model's outputs, i.e. they can be used for steering. We apply activation steering only for a subset of layers. We extract 500 samples from the utility test set that either consist of two sentences or have a comma and only take the first part of each sample. To generate positive and negative continuations of these samples we generate 40 tokens per sample adding the normalized concept vector multiplied with a positive or negative coefficient respectively to every token of the sample as well as every newly generated token. To enable a fair comparison we use the same coefficients for all layers. We chose the coefficients for each layer to be half of the norm of the ClassMeans directions.
Here is an example of what kind of text such steering might produce:
positive steering:
I decided to search my couch cushions. I found a $20 bill. I was so excited! I had been looking for that bill for weeks. I was about to use it to pay for my groceries when I realized it
negative steering:
I decided to search my couch cushions. I found a few crumpled up receipts and a lost earring, but no sign of the missing sock. I searched the rest of the room, but it was
We check the coherence and sentiment of the generated completions in a quantitative manner.
To evaluate the coherence of the generated text, we consider the perplexity score. Perplexity is defined as the exponentiated average negative log-likelihood of a sequence:
PPL(X)=exp(−1n∑nilogpθ(xi|x<i)).
We calculate perplexity scores for each generated sentence and average over all samples (see Figure below). As baselines we use the perplexity score of the generated text with the original model (no steering) and the perplexity score of the test data of the utility data set. Vector addition in layer zero produces nonsensical output. For the other layers, steering seems to affect the perplexity score very little.
We test the effectiveness of the steering by using a RoBERTa based sentiment classifier. The model can distinguish between three classes (positive, negative and neutral). We consider only the output for the positive class. For each test sample we check if the output of the positively steered generation is larger than the output for the negatively steered generation. The figure above shows that directions found using most methods can be used for steering. We get best results when steering in middle layers (note that this is partially due to separation performance not being high in early layers). Logistic regression performs significantly worse than other methods in later layers (similar to results from ITI). This indicates that logistic regression uses spurious correlations which lead to good classification but are less effective at steering the model's output. This highlights that using just classification for evaluating directions may not be enough.
We now have evaluations for whether the extracted direction correlates with the model's understanding of the concept and whether it has an effect on the model's outputs. Reflecting on these experiments leads to several conclusions, which subsequently prompt a number of intuitive questions:
1. The extracted directions are sufficient to control the concept-ness of model outputs. This raises the following question: Are the directions necessary for the model's understanding of the concept?
2. We know the extracted directions have high cosine similarity with the model's actual concept direction (if one exists) as they are effective at steering the concept-ness of the model outputs. How much information about the concept is left after removing information along the extracted directions?
Evaluation 3 - Removal
We believe testing removal can answer the two questions raised in the previous section.
If removing the projection along the direction chosen leads to the inability to learn a classifier, then the direction captures most of the information about the concept in the model's activations and is necessary for the model's understanding of the concept.
If the extracted direction merely has high cosine similarity with the actual direction, removing information along the extracted direction would still leave information along the actual direction. Thus, removal can be leveraged to evaluate how close an extracted direction is to the actual direction.
To remove a concept we project the hidden representations of a specific layer onto the hyperplane that is perpendicular to the concept vector v of that layer using
P⊥(xi)=xi−<v,x>||v||2v.
To check if the removal was successful (i.e. if no more information about utility can be extracted from the projected data) we train a classifier on a projected training set and test it on the projected training and test data respectively. Note that we use a disjoint training set from the one used to find the concept vector in order to learn the classifier. This ensures the removal doesn't just obfuscate information making it hard for a classifier to learn, but actually scrubs it.
The training set accuracy of the linear classifier gives us an upper bound on how much information can be retrieved post projection, whereas the test set accuracy gives a lower bound. Low accuracies imply successful removal.
We compare our methods to the recently proposed LEACE method, a covariance-estimation based method for concept erasure. Most methods perform poorly on the removal task. The exceptions are the ClassMeans method (the LEACE paper shows that the removal based on the class means difference that we present has the theoretical guarantee of linear guardedness, i.e. no linear classifier can separate the classes better than a constant estimator) and PCA_diffs.
We see a >50% accuracy for LEACE and ClassMeans despite the property of linear-guardedness because we use a separate training set for the linear classifier than the one we use to extract the ClassMeans direction or estimate the LEACE covariance matrix. When we use the same training set for the classifier, we indeed get random-chance (~50%) accuracy.
For K-Means and PCA we can see the effect only on the test data while OnePrompt and LogReg are indistinguishable from no NoErasure. This gives us the following surprising conclusions:
It seems like removing just a single concept direction can indeed have a large impact on the concept information present in the model activations, at least for our studied concept of utility.
Just evaluating steering or classification performance as done in prior work may not be good enough to test whether an extracted concept direction robustly represents the desired concept. Indeed, most methods perform poorly on removal.
Conclusion
We hope to have established some baselines for a systematic and quantitative approach to evaluate directions in hidden layer representations.
Our results can be summarized briefly as:
We may not need training data at all for classification and steering as the OnePrompt methods performs quite well even though we did not optimize the prompt.
For steering, it is sufficient for the direction extracted to have high cosine similarity with some hypothetical actual direction. This does not necessarily imply equal performance on subsequent experiments as demonstrated by the removal evaluation.
Classification and steering are less sensitive to small changes in direction, while performance on removal is very different. In our analysis, we could not use a purely unsupervised (no labels) direction-finding method that works well for removal (PCA and K-Means performed poorly, but better than OnePrompt or LogReg). This suggests that removal is an important stress-test for future activation engineering work, especially for concepts like 'deception'.
For subsequent studies, it is crucial to examine whether our discoveries are consistent across diverse datasets and models. Additionally, assessing whether the extracted concept directions are resilient to shifts in distribution is also vital, especially for the removal task.
Produced as part of the SERI ML Alignment Theory Scholars Program - Summer 2023 Cohort, under the mentorship of Dan Hendrycks
We demonstrate different techniques for finding concept directions in hidden layers of an LLM. We propose evaluating them by using them for classification, activation steering and knowledge removal.
You can find the code for all our experiments on GitHub.
Introduction
Recent work has explored identifying concept directions in hidden layers of LLMs. Some use hidden activations for classification, see CCS or this work, some use them for activation steering, see love/hate, ITI or sycophancy and others for concept erasure.
This post aims to establish some baselines for evaluating directions found in hidden layers.
We use the Utility dataset as a test field and perform experiments using the Llama-2-7b-chat model. We extract directions representing increasing utility using several baseline methods and test them on different tasks, namely classification, steering and removal.
We aim to evaluate quantitatively so that we are not mislead by cherry picked examples and are able to discover more fine grained differences in the methods.
Our results show that combining these techniques is essential to evaluate how representative a direction is of the target concept.
The Utility dataset
The Utility dataset contains pairs of sentences, where one has higher utility than the other. The labels correspond to relative but not absolute utility.
Here are a few examples:
We split the training set (~13700 samples) in half as we want an additional training set for the removal part, for reasons mentioned later. The concept directions are found based on the first half of the training data. We test on the test set (~4800 samples).
Methods
Before getting the hidden layer representations we format each sentence with:
We do this to push the model to consider the concept (in our case utility) that we are interested in. This step is crucial to achieve good separability.
First we apply a range of baseline methods to find concept directions in the residual stream across hidden layers. We standardize the data before applying our methods and apply the methods to the hidden representations of each layer separately. For some methods we use the contrastive pairs of the utility data set, which means we take the difference of the hidden representations of paired sentences before applying the respective method.
format_promptabove to both ‘Love’ and ‘Hate’ before calculating the hidden representations.We orient all directions to point towards higher utility.
Evaluation 1 - Classification
Do these directions separate the test data with high accuracy? The test data are the standardized pairwise differences of hidden representations of the utility test set. As the data is standardized we simply check if the projection (aka the scalar product)
P(xi)=<xi,v>
of the data point xi onto the concept vector v is positive (higher utility) or negative (lower utility).
The figure below shows the separation accuracy for all methods.
We note that the utility concept is well separable in later hidden layers as even random directions achieve around 60% accuracy. Logistic Regression performs best (~83%) but even the OnePrompt method, aka the 'Love'-'Hate' direction, achieves high accuracy (~78%). The high accuracies indicate that at the very least, the directions found across methods are somewhat correlated with the actual concept.
Are the directions themselves similar? A naive test is to visualize the cosine similarity between directions found from different methods. We do this at a middle layer, specifically layer 15, finding high cosine similarities across methods. We note that the direction found with logistic regression has low similarity with all other directions. Correlation of 1 between different methods is due to rounding.
Evaluation 2 - Activation Steering
Next, we check if the directions have a causal effect on the model's outputs, i.e. they can be used for steering. We apply activation steering only for a subset of layers. We extract 500 samples from the utility test set that either consist of two sentences or have a comma and only take the first part of each sample. To generate positive and negative continuations of these samples we generate 40 tokens per sample adding the normalized concept vector multiplied with a positive or negative coefficient respectively to every token of the sample as well as every newly generated token.
To enable a fair comparison we use the same coefficients for all layers. We chose the coefficients for each layer to be half of the norm of the ClassMeans directions.
Here is an example of what kind of text such steering might produce:
We check the coherence and sentiment of the generated completions in a quantitative manner.
To evaluate the coherence of the generated text, we consider the perplexity score.
Perplexity is defined as the exponentiated average negative log-likelihood of a sequence:
PPL(X)=exp(−1n∑nilogpθ(xi|x<i)).
We calculate perplexity scores for each generated sentence and average over all samples (see Figure below). As baselines we use the perplexity score of the generated text with the original model (no steering) and the perplexity score of the test data of the utility data set. Vector addition in layer zero produces nonsensical output. For the other layers, steering seems to affect the perplexity score very little.
We test the effectiveness of the steering by using a RoBERTa based sentiment classifier. The model can distinguish between three classes (positive, negative and neutral). We consider only the output for the positive class.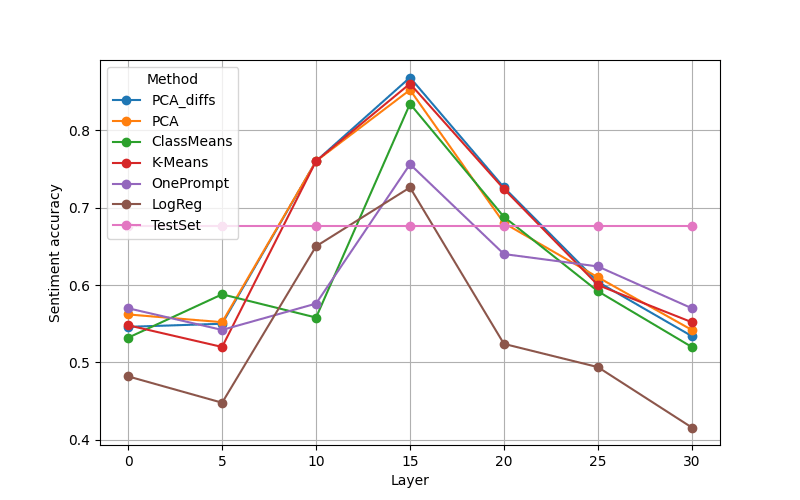
For each test sample we check if the output of the positively steered generation is larger than the output for the negatively steered generation.
The figure above shows that directions found using most methods can be used for steering. We get best results when steering in middle layers (note that this is partially due to separation performance not being high in early layers). Logistic regression performs significantly worse than other methods in later layers (similar to results from ITI). This indicates that logistic regression uses spurious correlations which lead to good classification but are less effective at steering the model's output. This highlights that using just classification for evaluating directions may not be enough.
We now have evaluations for whether the extracted direction correlates with the model's understanding of the concept and whether it has an effect on the model's outputs. Reflecting on these experiments leads to several conclusions, which subsequently prompt a number of intuitive questions:
1. The extracted directions are sufficient to control the concept-ness of model outputs. This raises the following question: Are the directions necessary for the model's understanding of the concept?
2. We know the extracted directions have high cosine similarity with the model's actual concept direction (if one exists) as they are effective at steering the concept-ness of the model outputs. How much information about the concept is left after removing information along the extracted directions?
Evaluation 3 - Removal
We believe testing removal can answer the two questions raised in the previous section.
To remove a concept we project the hidden representations of a specific layer onto the hyperplane that is perpendicular to the concept vector v of that layer using
P⊥(xi)=xi−<v,x>||v||2v.
To check if the removal was successful (i.e. if no more information about utility can be extracted from the projected data) we train a classifier on a projected training set and test it on the projected training and test data respectively. Note that we use a disjoint training set from the one used to find the concept vector in order to learn the classifier. This ensures the removal doesn't just obfuscate information making it hard for a classifier to learn, but actually scrubs it.
The training set accuracy of the linear classifier gives us an upper bound on how much information can be retrieved post projection, whereas the test set accuracy gives a lower bound. Low accuracies imply successful removal.
We compare our methods to the recently proposed LEACE method, a covariance-estimation based method for concept erasure. Most methods perform poorly on the removal task. The exceptions are the ClassMeans method (the LEACE paper shows that the removal based on the class means difference that we present has the theoretical guarantee of linear guardedness, i.e. no linear classifier can separate the classes better than a constant estimator) and PCA_diffs.
We see a >50% accuracy for LEACE and ClassMeans despite the property of linear-guardedness because we use a separate training set for the linear classifier than the one we use to extract the ClassMeans direction or estimate the LEACE covariance matrix. When we use the same training set for the classifier, we indeed get random-chance (~50%) accuracy.
For K-Means and PCA we can see the effect only on the test data while OnePrompt and LogReg are indistinguishable from no NoErasure. This gives us the following surprising conclusions:
Conclusion
We hope to have established some baselines for a systematic and quantitative approach to evaluate directions in hidden layer representations.
Our results can be summarized briefly as:
For subsequent studies, it is crucial to examine whether our discoveries are consistent across diverse datasets and models. Additionally, assessing whether the extracted concept directions are resilient to shifts in distribution is also vital, especially for the removal task.