A more factual and descriptive phrase for "grokking" would be something like "eventual recovery from overfitting".
Ooh I do like this. But it's important to have a short handle for it too.
I've been using "delayed generalisation", which I think is more precise than "grokking", places the emphasis on the delay rather the speed of the transition, and is a short phrase.
Small point/question, Quintin -- when you say that you "can fully avoid grokking on modular arithmetic", in the colab notebook you linked to in that paragraph it looks like you just trained for 3e4 steps. Without explicit regularization, I wouldn't have expected your network to generalize in that time (it might take 1e6 or 1e7 steps for networks to fully generalize). What point were you trying to make there? By "avoid grokking", do you mean (1) avoid generalization or (2) eliminate the time delay between memorization and generalization. I'd be pretty interested if you achieved (2) while not using explicit regularization.
Honestly I'd be surprised if you could achieve (2) even with explicit regularization, specifically on the modular addition task.
(You can achieve it by initializing the token embeddings to those of a grokked network so that the representations are appropriately structured; I'm not allowing things like that.)
EDIT: Actually, Omnigrok does this by constraining the parameter norm. I suspect this is mostly making it very difficult for the network to strongly memorize the data -- given the weight decay parameter the network "tries" to learn a high-param norm memorizing solution, but then repeatedly runs into the parameter norm constraint -- and so creates a very strong reason for the network to learn the generalizing algorithm. But that should still count as normal regularization.
If you train on infinite data, I assume you'd not see a delay between training and testing, but you'd expect a non-monotonic accuracy curve that looks kind of like the test accuracy curve in the finite-data regime? So I assume infinite data is also cheating?
I expect a delay even in the infinite data case, I think?
Although I'm not quite sure what you mean by "infinite data" here -- if the argument is that every data point will have been seen during training, then I agree that there won't be any delay. But yes training on the test set (even via "we train on everything so there is no possible test set") counts as cheating for this purpose.
I mean (1). You can see as much in the figure displayed in the linked notebook:
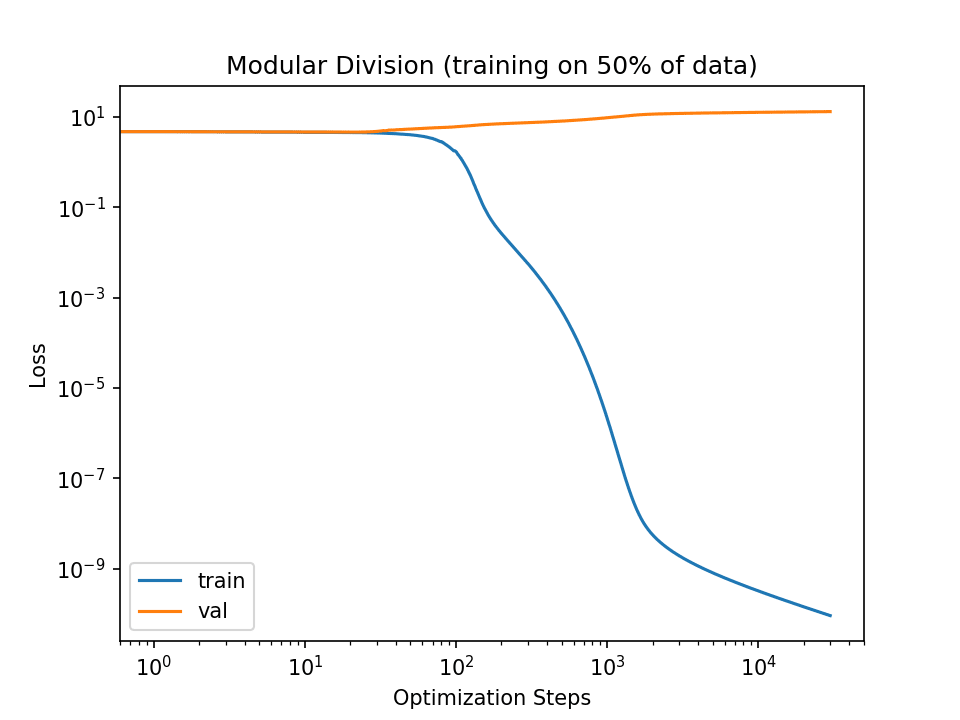
Note the lack of decrease in the val loss.
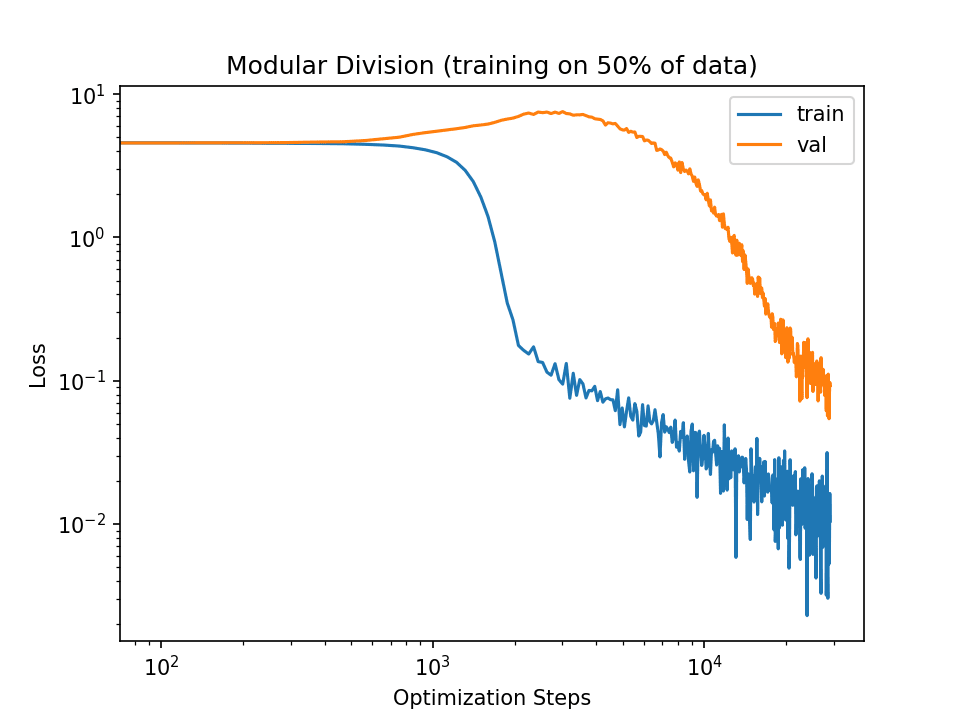
I only train for 3e4 steps because that's sufficient to reach generalization with implicit regularization. E.g., here's the loss graph I get if I set the batch size down to 50:
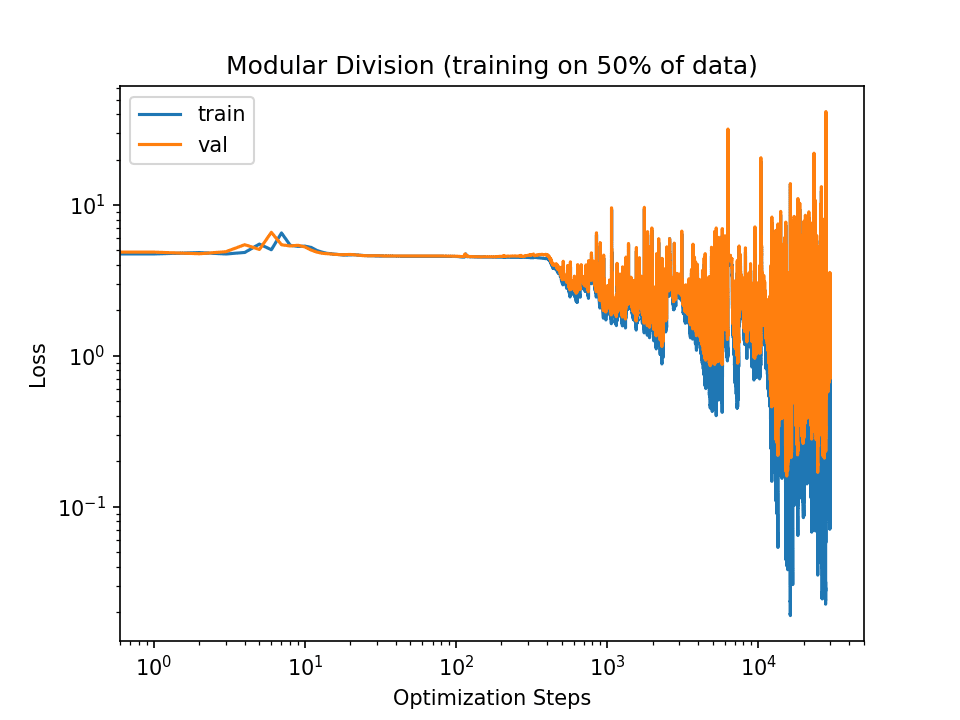
Setting the learning rate to 7e-2 also allows for generalization within 3e4 steps (though not as stably):
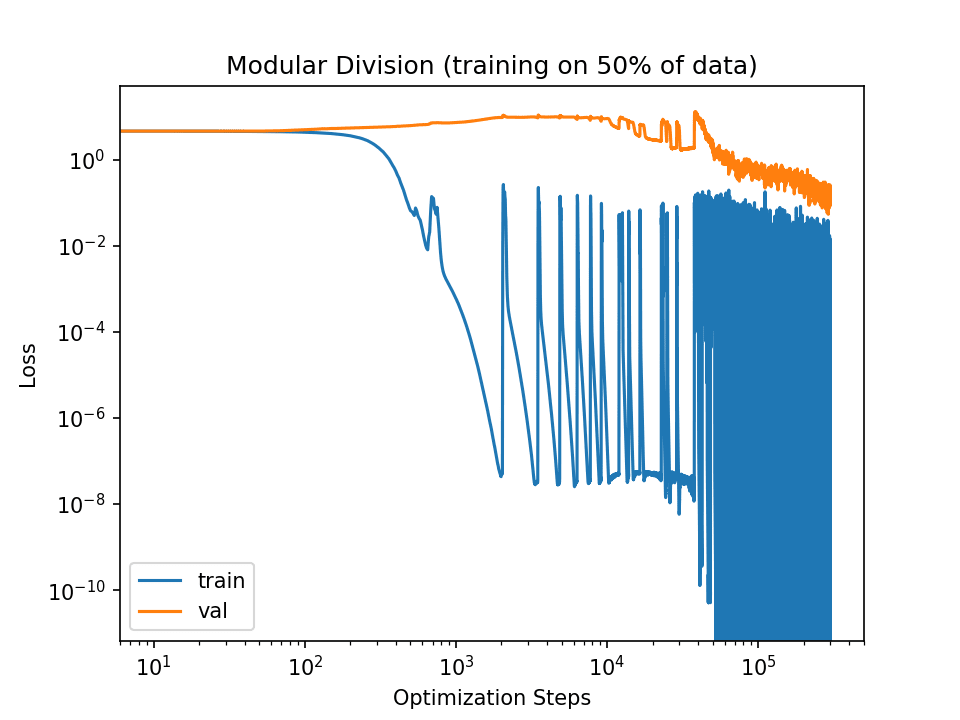
The slingshot effect does take longer than 3e4 steps to generalize:
Broadly agree with the takes here.
However, these results seem explainable by the widely-observed tendency of larger models to learn faster and generalize better, given equal optimization steps.
This seems right and I don't think we say anything contradicting it in the paper.
I also don't see how saying 'different patterns are learned at different speeds' is supposed to have any explanatory power. It doesn't explain why some types of patterns are faster to learn than others, or what determines the relative learnability of memorizing versus generalizing patterns across domains. It feels like saying 'bricks fall because it's in a brick's nature to move towards the ground': both are repackaging an observation as an explanation.
The idea is that the framing 'learning at different speeds' lets you frame grokking and double descent as the same thing. More like generalizing 'bricks move towards the ground' and 'rocks move towards the ground' to 'objects move towards the ground'. I don't think we make any grand claims about explaining everything in the paper, but I'll have a look and see if there's edits I should make - thanks for raising these points.
[Thanks to support from Cavendish Labs and a Lightspeed grant, I've been able to restart the Quintin's Alignment Papers Roundup sequence.]
Introduction
Grokking refers to an observation by Power et al. (below) that models trained on simple modular arithmetic tasks would first overfit to their training data and achieve nearly perfect training loss, but that training well past the point of overfitting would eventually cause the models to generalize to unseen test data. The rest of this post discusses a number of recent papers on grokking.
Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets
My opinion:
When I first read this paper, I was very excited. It seemed like a pared-down / "minimal" example that could let us study the underlying mechanism behind neural network generalization. You can read more of my initial opinion on grokking in the post Hypothesis: gradient descent prefers general circuits.
I now think I was way too excited about this paper, that grokking is probably a not-particularly-important optimization artifact, and that grokking is no more connected to the "core" of deep learning generalization than, say, the fact that it's possible for deep learning to generalize from an MNIST training set to the testing set.
I also think that using the word "grokking" was anthropomorphizing and potentially misleading (like calling the adaptive information routing component of a transformer model its "attention"). Evocative names risk letting the connotations of the name filter into the analysis of the object being named. E.g.,
I've heard several people say things like:
A more factual and descriptive phrase for "grokking" would be something like "eventual recovery from overfitting". I've personally found that using more neutral mental labels for "grokking" helps me think about it more clearly. It lets me more easily think about just the empirical results of grokking experiments and their implications, without priming myself with potentially unwarranted connotations.
An aside on the suddenness of grokking:
People often talk as though grokking is a sudden process. This isn't necessarily true. For example, the grokking shown in this plot above is not sudden. Rather, the log base-10 scale of the x-axis makes it look sudden. If you actually measure the graph, you'll see that the grokking phase takes up the majority of the training steps (between ~80% and 95%, depending on when you place the start / end of the grokking period).
To be clear, grokking can be sudden. Rapid grokking most often happens when training with an explicit regularizer such as weight decay (e.g., in the below paper). However, relying on weaker implicit regularizers can lead to much more gradual grokking. The plot above shows a training run that used the slingshot mechanism as its source of implicit regularization, which occurs when numerical underflow errors in calculating training losses create anomalous gradients which adaptive gradient optimizers like Adam propagate. This can act as a 'poor man's gradient noise' and thus a source of regularization.
From personal experiments, I've found that avoiding explicit weight decay regularization, combined with minimizing implicit regularization by using a low learning rate alongside full batch gradient descent, and using 64 bit precision for loss calculations, that I can fully avoid grokking on modular arithmetic.
A Mechanistic Interpretability Analysis of Grokking
My opinion:
This post provides an awesome example of mechanistic interpretability analysis to understand how models use Fourier transforms and trig identities to build general solutions to modular arithmetic problems, and tracks how that solution develops over time as the model groks. The post also connects grokking to the much more general and widespread phenomena of phase changes in ML training.
However, I don't think that grokking is a the best testbed for studying phase changes more generally. We have much more realistic deep learning systems that undergo phase transitions, such as during double descent, the formation of induction heads and emergent outliers in language models, or (possibly) OpenFold's series of sequential transitions in as its outputs move from being zero dimensional, to one dimensional, to two dimensional, and finally to three dimensional.
Towards Understanding Grokking: An Effective Theory of Representation Learning
My opinion:
I really liked the illustrations of how the representation spaces differ before and after grokking:
Generalization seems to correspond to simpler and smoother geometries of the representation spaces. This meshes with another perspective that points to geometric simplicity / smoothness as one of the key inductive biases driving generalization in deep learning, which also seems inline with Power et al.'s finding (in section A.5) that post-grokking solutions correspond to flatter local minima.
However, I think the key result of this paper is that it's possible to avoid grokking completely by choosing different training hyperparameters (see below). From a capabilities perspective, grokking is a mistake. The ideal network doesn't grok. Rather, it starts generalizing immediately.
Omnigrok: Grokking Beyond Algorithmic Data
My opinion:
The above two papers suggest grokking is a consequence of moderately bad training setups. I.e., training setups that are bad enough that the model starts out by just memorizing the data, but which also contain some sort of weak regularization that eventually corrects this initial mistake.
If that story is true, then I think it casts doubt on the relevance of studying grokking to AGI safety. Presumably, an AGI's training process is going to have a pretty good setup. Why should we expect results from studying grokking to transfer?
E.g., Omnigrok indicates that the reason we don't see grokking in MNIST is because we've extensively tuned the training setups for MNIST models (including their initialization processes), and conversely, the reason we do see grokking in algorithmic tasks is because we haven't extensively tuned the training setups for such models. Given this, how useful should we expect algorithmic grokking results to be for improving / tuning / controlling MNIST models?
A Tale of Two Circuits: Grokking as Competition of Sparse and Dense Subnetworks
My opinion:
This paper doesn't seem too novel in its implications, but it does seem to confirm some of the findings in A Mechanistic Interpretability Analysis of Grokking and Omnigrok: Grokking Beyond Algorithmic Data.
Similar to A Mechanistic Interpretability Analysis of Grokking, this paper finds two competing solutions inside the network, and that grokking occurs as a phase transition where the general solution takes over from the memorizing solution.
In Omnigrok, decreasing the initialization norms leads to immediate generalization. This paper finds that grokking corresponds to increasing weight norms of the generalizing subnetwork and decreasing weight norms for the rest of the network:
Unifying Grokking and Double Descent
My opinion:
I find this paper somewhat dubious. Their key novel result, that grokking can happen with increasing model size, is illustrated in their figure 4:
However, these results seem explainable by the widely-observed tendency of larger models to learn faster and generalize better, given equal optimization steps.
I also don't see how saying 'different patterns are learned at different speeds' is supposed to have any explanatory power. It doesn't explain why some types of patterns are faster to learn than others, or what determines the relative learnability of memorizing versus generalizing patterns across domains. It feels like saying 'bricks fall because it's in a brick's nature to move towards the ground': both are repackaging an observation as an explanation.
Grokking of Hierarchical Structure in Vanilla Transformers
My opinion:
I liked this paper a lot.
Firstly, its use of language as a domain (even if limited to synthetic data) makes it more relevant to the current paradigm for making progress on AGI.
Secondly, many grokking experiments compare "generalization versus memorization". I.e., they compare the most complicated possible solution[1] to the training data to the least. Realistically, we're more interested in which of many possible generalizations a deep learning model develops, where the relative simplicities of the generalizations may not be clear.
Finally, this paper finds phenomena that don't fit with prior grokking results:
A full account of generalization for realistic problems probably involves interactions between optimizer, architecture, and dataset properties. The U-shaped loss results suggest this paper is starting to probe at how the inductive biases of a given architecture do or do not match the structure of a dataset, and how that interaction ties into the resulting generalization patterns (2/3 isn't a bad start!).
Conclusion
I don't currently think that grokking is particularly core to the underlying mechanisms of deep learning generalization. That's not to say grokking has nothing to do with generalization, or that we couldn't possibly learn more about generalization by studying grokking. Rather, I don't think the current evidence implies that studying grokking would be particularly more fruitful than, say, studying generalization on CIFAR10, TinyStories, or full-on language modeling.
I also worry that the extremely simplified domains in which grokking is often studied will lead to biased results that don't generalize to more realistic setups. This makes me more excited about attempts to analyze grokking in less-simplified domains.
Future
I intend to restart this series. I won't be aiming for a weekly update schedule, but I will aim to release at least two more before the end of the summer.
My next topic will be on runtime interventions in neural net cognition, similar to Steering GPT-2-XL by adding an activation vector. However, feel free to suggest other topics for future roundups.
If the goal is to better understand how neural networks pick between out of distribution generalizations, then a solution with zero generalization capacity at all (memorization) feels like a degenerate case.