I'm a Postdoctoral Research Fellow at Oxford University's Global Priorities Institute.
Previously, I was a Philosophy Fellow at the Center for AI Safety.
So far, my work has mostly been about the moral importance of future generations. Going forward, it will mostly be about AI.
You can email me at elliott.thornley@philosophy.ox.ac.uk.
Posts
Wikitag Contributions
I think it’s going to be very typical for different actions to have trajectories that are mutually non-dominant (such as in the example). It matters a lot how you decide such cases, and I expect that almost all such ways of deciding are catastrophic.
But suppose I’m wrong, and timestep-dominance is always relevant.
My claim isn't that Timestep Dominance is always relevant. It's that Timestep Dominance rules out all instances of resisting shutdown.
I agree that many pairs of available lotteries are going to be mutually non-dominant. For those cases, Sami and I propose that the agent choose by maximizing expected utility. Can you say what you expect the problem there to be?
Suppose that, assuming the shutdown button didn’t exist, the fastest pathway to paperclips involves instantiating a paperclip-seeking AI on an unsecured server in Singapore. Suppose that it takes 99,000 keystrokes to create an IPP agent, but only 55,000 keystrokes to create a basic VNM-rational agent with a short enough time horizon that it produces more paperclips quickly, in expectation (because VNM agents are both simpler and less likely to be shut down by angry humans). The shutdown button does, in fact exist, but the agent’s actions might be hard to notice, such that by the time anyone has realized that something went wrong, the agent already created a sub-agent, effectively making the stop-button useless.
I talk about the issue of creating corrigible subagents here. What do you think of that?
Note also a general nice feature of TD-agents: they won’t pay costs to hide their bad behaviour, because paying these costs is timestep-dominated by not paying them. So if a TD-agent does try to create an incorrigible paperclipper, it won't hide that fact if doing so is at all costly.
While active resistance seems like the scariest part of incorrigibility, an incorrigible agent that’s not actively resisting still seems likely to be catastrophic.
Can you say more about this? It doesn't seem likely to me.
One more thing I'll say: the IPP leaves open the content of the agent's preferences over same-length trajectories. One pattern of preferences you could try to train in is the kind of corrigibility that you talk about elsewhere in your sequence. That'd give you two lines of defence against incorrigibility.
I think your 'Incomplete preferences' section makes various small mistakes that add up to important misunderstandings.
The utility maximization concept largely comes from the VNM-utility-theorem: that any policy (i.e. function from states to actions) which expresses a complete set of transitive preferences (which aren’t sensitive to unused alternatives) over lotteries is able to be described as an agent which is maximizing the expectation of some real-valued utility function over outcomes.
I think you intend 'sensitive to unused alternatives' to refer to the Independence axiom of the VNM theorem, but VNM Independence isn't about unused alternatives. It's about lotteries that share a sublottery. It's Option-Set Independence (sometimes called 'Independence of Irrelevant Alternatives') that's about unused alternatives.
On the surface, the axioms of VNM-utility seem reasonable to me
To me too! But the question isn't whether they seem reasonable. It's whether we can train agents that enduringly violate them. I think that we can. Coherence arguments give us little reason to think that we can't.
unused alternatives seem basically irrelevant to choosing between superior options
Yes, but this isn't Independence. And the question isn't about what seems basically irrelevant to us.
agents with intransitive preferences can be straightforwardly money-pumped
Not true. Agents with cyclic preferences can be straightforwardly money-pumped. The money-pump for intransitivity requires the agent to have complete preferences.
as long as the resources are being modeled as part of what the agent has preferences about
Yes, but the concern is whether we can instil such preferences. It seems like it might be hard to train agents to prefer to spend resources in pursuit of their goals except in cases where they would do so by resisting shutdown.
Thornley, I believe, thinks he’s proposing a non-VNM rational agent. I suspect that this is a mistake on his part that stems from neglecting to formulate the outcomes as capturing everything that he wants.
You can, of course, always reinterpret the objects of preference so that the VNM axioms are trivially satisfied. That's not a problem for my proposal. See:
Thanks, Lucius. Whether or not decision theory as a whole is concerned only with external behaviour, coherence arguments certainly aren’t. Remember what the conclusion of these arguments is supposed to be: advanced agents who start off not being representable as EUMs will amend their behaviour so that they are representable as EUMs, because otherwise they’re liable to pursue dominated strategies.
Now consider an advanced agent who appears not to be representable as an EUM: it’s paying to trade vanilla for strawberry, strawberry for chocolate, and chocolate for vanilla. Is this agent pursuing a dominated strategy? Will it amend its behaviour? It depends on the objects of preference. If objects of preference are ice-cream flavours, the answer is yes. If the objects of preference are sequences of trades, the answer is no. So we have to say something about the objects of preference in order to predict the agent’s behaviour. And the whole point of coherence arguments is to predict agents’ behaviour.
And once we say something about the objects of preference, then we can observe agents violating Completeness and acting in accordance with policies like ‘if I previously turned down some option X, I will not choose any option that I strictly disprefer to X.’ This doesn't require looking into the agent or saying anything about its algorithm or anything like that. It just requires us to say something about the objects of preference and to watch what the agent does from the outside. And coherence arguments already commit us to saying something about the objects of preference. If we say nothing, we get no predictions out of them.
The pattern of how an agent chooses options are that agent’s preferences, whether we think of them as such or whether they’re conceived as a decision rule to prevent being dominated by expected-utility maximizers!
You can define 'preferences' so that this is true, but then it need not follow that agents will pay costs to shift probability mass away from dispreferred options and towards preferred options. And that's the thing that matters when we're trying to create a shutdownable agent. We want to ensure that agents won't pay costs to influence shutdown-time.
Also, take your decision-tree and replace 'B' with 'A-'. If we go with your definition, we seem to get the result that expected-utility-maximizers prefer A- to A (because they choose A- over A on Monday). But that doesn't sound right, and so it speaks against the definition.
I think it’s interesting to note that we’re also doing something like throwing out the axiom of independence from unused alternatives
Not true. The axiom we're giving up is Decision-Tree Separability. That's different to VNM Independence, and different to Option-Set Independence. It might be hard to train agents that enduringly violate VNM Independence and/or Option-Set Independence. It doesn't seem so hard to train agents that enduringly violate Decision-Tree Separability.
In other words, if you wake up as this kind of agent on Monday, the way you cash-out your partial ordering over outcomes depends on your memory/model of what happened on Sunday.
Yes, nice point. Kinda weird? Maybe. Difficult to create artificial agents that do it? Doesn't seem so.
But notice that this refactor effectively turns Thornley’s agent into an agent with a set of preferences which satisfies the completeness and independence axioms of VNM
Yep, you can always reinterpret the objects of preference so that the VNM axioms are trivially satisfied.That's not a problem for my proposal.
the point is that “incomplete preferences” combined with a decision making algorithm which prevents the agent’s policy from being strictly dominated by an expected utility maximizer ends up, in practice, as isomorphic to an expected utility maximizer which is optimizing over histories/trajectories.
Not true. As I say elsewhere:
And an agent abiding by the Caprice Rule can’t be represented as maximising utility, because its preferences are incomplete. In cases where the available trades aren’t arranged in some way that constitutes a money-pump, the agent can prefer (/reliably choose) A+ over A, and yet lack any preference between (/stochastically choose between) A+ and B, and lack any preference between (/stochastically choose between) A and B. Those patterns of preference/behaviour are allowed by the Caprice Rule.
I want to consider how there’s a common misunderstanding of “outcomes” in the VNM-sense as needing to be about physical facts of the future universe (such as number of paperclips) rather than as potentially including historical facts, such as which options were abandoned or whether the agent took the default action. This is extremely relevant for corrigibility since one of the key ideas in my strategy is to shift the AI’s preferences from being about things like whether the button is pushed to being about whether the agent consistently maintained a certain kind of relationship with the principal during the relevant period.
Same point here as above. You can get any agent to satisfy the VNM axioms by enriching the objects of preference. A concern is that these more complex preferences are harder to reliably train into your agent.
Thanks, this comment is also clarifying for me.
My guess is that a corrigibility-centric training process says 'Don't get the ice cream' is the correct completion, whereas full alignment says 'Do'. So that's an instance where the training processes for CAST and FA differ. How about DWIM? I'd guess DWIM also says 'Don't get the ice cream', and so seems like a closer match for CAST.
Corrigibility is, at its heart, a relatively simple concept compared to good alternatives.
I don't know about this, especially if obedience is part of corrigibility. In that case, it seems like the concept inherits all the complexity of human preferences. And then I'm concerned, because as you say:
When a training target is complex, we should expect the learner to be distracted by proxies and only get a shadow of what’s desired.
I think obedience is an emergent behavior of corrigibility.
In that case, I'm confused about how the process of training an agent to be corrigible differs from the process of training an agent to be fully aligned / DWIM (i.e. training the agent to always do what we want).
And that makes me confused about how the proposal addresses problems of reward misspecification, goal misgeneralization, deceptive alignment, and lack of interpretability. You say some things about gradually exposing agents to new tasks and environments (which seems sensible!), but I'm concerned that that by itself won't give us any real assurance of corrigibility.
Thanks, appreciate this!
It's unclear to me what the expectation in Timestep Dominance is supposed to be with respect to. It doesn't seem like it can be with respect to the agent's subjective beliefs as this would make it even harder to impart.
I propose that we train agents to satisfy TD with respect to their subjective beliefs. I’m guessing that you think that this kind of TD would be hard to impart because we don’t know what the agent believes, and so don’t know whether a lottery is timestep-dominated with respect to those beliefs, and so don’t know whether to give the agent lower reward for choosing that lottery.
But (it seems to me) we can be quite confident that the agent has certain beliefs, because these beliefs are necessary for performing well in training. For example, we can be quite confident that the agent believes that resisting shutdown costs resources, that the resources spent on resisting shutdown can’t also be spent on directly pursuing utility at a timestep, and so on.
And if we can be quite confident that the agent has these accurate beliefs about the environment, then we can present the agent with lotteries that are actually timestep-dominated (according to the objective probabilities decided by the environment) and be quite confident that these lotteries are also timestep-dominated with respect to the agent’s beliefs. After all, we don’t need to know the agent’s beliefs with any great detail or precision to tell whether a lottery is timestep-dominated with respect to those beliefs. We just need to know whether the agent believes that the lottery involves spending resources only to shift probability mass between shutdowns at different timesteps. My proposal is that we present the agent with lotteries in which this is actually the case (according to the objective probabilities decided by the environment) and use the fact that capable agents’ beliefs will reflect this actuality.
Imparting TD preferences seems hard
The prosaic version of this proposal assumes that you can impart timestep dominance preferences into AIs in ways which will robustly generalize. This seems unlikely to be true in general (in the absence of additional technology) and if we did have the property, we could solve safety issues in some other way (e.g. robustly generalizing honesty). So you'll need to argue that timestep dominance is particularly easy to robustly impart relative to other preferences. I can see some arguments for timestep dominance being particularly easy to robustly impart, but they don't seem very strong to me.
Yep, I claim that it’s easier to robustly impart POST and Timestep Dominance than it is to robustly impart things like honesty. And that’s because (it seems to me) we can train for POST and Timestep Dominance in ways that largely circumvent the problems of reward misspecification, goal misgeneralization, and deceptive alignment. I argue that case in section 19 but in brief: POST and TD seem easy to reward accurately, seem simple, and seem never to give agents a chance to learn goals that incentivise deceptive alignment. By contrast, none of those things seem true of a preference for honesty. Can you explain why those arguments don’t seem strong to you?
Suppose that Clippy is a TD-agent which cares solely about the long run number of paperclips, but subject to a TD constraint. That is, it always prefers trajectory X over Y if for all shutdown timings X gives a >= number of paperclips than Y and X gives a > number of paperclips for some timing.
Now, consider the following proposed action for Clippy: "In a stealthy manner, construct a successor agent which pursues long run paperclips at all costs (and which isn't subject to a shutdown button, but still has TD constraints wrt. to the original Clippy's shutdown button)." This agent is implicitly resisting shutdown as it's constructing the sub-agent stealthily. So, shouldn't this action be Timestep Dominanted by "In whatever way is most expedient (but not necessarily stealthy), construct a successor agent". I claim not, because if we condition on the AI not being shutdown prior to constructing the agent (a particular shutdown time conditional), it will be worse for clippy if humans know that it is constructing a successor as then humans will have an easier time fighting the successor. In other words, having humans know that you're constructing a successor has two effects: they'll fight your successor and they'll shut you down. If we condition on not being shutdown, then they'll still fight your successor, so Clippy would prefer being stealthy in the no shut down conditional. Thus, being stealthy isn't Timestep Dominated by changing the action to avoid resisting shutdown. (And once the successor is constructed, shutting down Clippy has no effect on the long run number of paperclips (let's suppose).)
(You should think of this counterexample as a worst case theory counterexample. The exact assumptions might not be realistic, but it points at a broader class of issues.)
Yes, nice point; I plan to think more about issues like this. But note that in general, the agent overtly doing what it wants and not getting shut down seems like good news for the agent’s future prospects. It suggests that we humans are more likely to cooperate than the agent previously thought. That makes it more likely that overtly doing the bad thing timestep-dominates stealthily doing the bad thing.
Timestep dominance is maybe crippling
I'm most uncertain here, but my current guess would be that any sort of absolute constraint like this is crippling. I've thought through some cases and this is my current guess, but I'm by no means confident.
Can you say more about these cases? Timestep Dominance doesn’t rule out making long-term investments or anything like that, so why crippling?
Great post! Lots of cool ideas. Much to think about.
systems with incomplete preferences will tend to contract/precommit in ways which complete their preferences.
Point is: non-dominated strategy implies utility maximization.
But I still think both these claims are wrong.
And that’s because you only consider one rule for decision-making with incomplete preferences: a myopic veto rule, according to which the agent turns down a trade if the offered option is ranked lower than its current option according to one or more of the agent’s utility functions.
The myopic veto rule does indeed lead agents to pursue dominated strategies in single-sweetening money-pumps like the one that you set out in the post. I made this point in my coherence theorems post:
John Wentworth’s ‘Why subagents?’ suggests another policy for agents with incomplete preferences: trade only when offered an option that you strictly prefer to your current option. That policy makes agents immune to the single-souring money-pump. The downside of Wentworth’s proposal is that an agent following his policy will pursue a dominated strategy in single-sweetening money-pumps, in which the agent first has the opportunity to trade in A for B and then (conditional on making that trade) has the opportunity to trade in B for A+. Wentworth’s policy will leave the agent with A when they could have had A+.
But the myopic veto rule isn’t the only possible rule for decision-making with incomplete preferences. Here’s another. I can’t think of a better label right now, so call it ‘Caprice’ since it’s analogous to Brian Weatherson’s rule of the same name for decision-making with multiple probability functions:
- Don’t make a sequence of trades (with result X) if there’s another available sequence (with result Y) such that Y is ranked at least as high as X on each of your utility functions and ranked higher than X on at least one of your utility functions. Choose arbitrarily/stochastically among the sequences of trades that remain.
The Caprice Rule implies the policy that I suggested in my coherence theorems post:
- If I previously turned down some option Y, I will not settle on any option that I strictly disprefer to Y.
And that makes the agent immune to single-souring money-pumps (in which the agent first has the opportunity to trade in A for B and then (conditional on making that trade) has the opportunity to trade in B for A-).
The Caprice Rule also implies the following policy:
- If in future I will be able to settle on some option Y, I will not instead settle on any option that I strictly disprefer to Y.
And that makes the agent immune to single-sweetening money-pumps like the one that you discuss. If the agent recognises that – conditional on trading in mushroom (analogue in my post: A) for anchovy (B) – they will be able to trade in anchovy (B) for pepperoni (A+), then they will make at least the first trade, and thereby avoid pursuing a dominated strategy. As a result, an agent abiding by the Caprice Rule can’t shift probability mass from mushroom (A) to pepperoni (A+) by probabilistically precommitting to take certain trades in a way that makes their preferences complete. The Caprice Rule already does the shift.
And an agent abiding by the Caprice Rule can’t be represented as maximising utility, because its preferences are incomplete. In cases where the available trades aren’t arranged in some way that constitutes a money-pump, the agent can prefer (/reliably choose) A+ over A, and yet lack any preference between (/stochastically choose between) A+ and B, and lack any preference between (/stochastically choose between) A and B. Those patterns of preference/behaviour are allowed by the Caprice Rule.
For a Caprice-Rule-abiding agent to avoid pursuing dominated strategies in single-sweetening money-pumps, that agent must be non-myopic: specifically, it must recognise that trading in A for B and then B for A+ is an available sequence of trades. And you might think that this is where my proposal falls down: actual agents will sometimes be myopic, so actual agents can’t always use the Caprice Rule to avoid pursuing dominated strategies, so actual agents are incentivised to avoid pursuing dominated strategies by instead probabilistically precommitting to take certain trades in ways that make their preferences complete (as you suggest).
But there’s a problem with this response. Suppose an agent is myopic. It finds itself with a choice between A and B, and it chooses A. As a matter of fact, if it had chosen B, it would have later been offered A+. Then the agent leaves with A when it could have had A+. But since the agent is myopic, it won’t be aware of this fact, and so note two things. First, it’s unclear whether the agent’s behaviour deserves the name ‘dominated strategy’. The agent pursues a dominated strategy only in the same sense that I pursue a dominated strategy when I fail to buy a lottery ticket that (unbeknownst to me) would have won. Second and more importantly, the agent’s failure to get A+ won’t lead the agent to change its preferences, since it’s myopic and so unaware that A+ was available.
And so we seem to have a dilemma for money-pumps for completeness. In money-pumps where the agent is non-myopic about the available sequences of trades, the agent can avoid pursuit of dominated strategies by acting in accordance with the Caprice Rule. In money-pumps where the agent is myopic, failing to get A+ exerts no pressure on the agent to change its preferences, since the agent is not aware that it could have had A+.
You recognise this in the post and so set things up as follows: a non-myopic optimiser decides the preferences of a myopic agent. But this means your argument doesn’t vindicate coherence arguments as traditionally conceived. Per my understanding, the conclusion of coherence arguments was supposed to be: you can’t rely on advanced agents not to act like expected-utility-maximisers, because even if these agents start off not acting like EUMs, they’ll recognise that acting like an EUM is the only way to avoid pursuing dominated strategies. I think that’s false, for the reasons that I give in my coherence theorems post and in the paragraph above. But in any case, your argument doesn’t give us that conclusion. Instead, it gives us something like: a non-myopic optimiser of a myopic agent can shift probability mass from less-preferred to more-preferred outcomes by probabilistically precommitting the agent to take certain trades in a way that makes its preferences complete. That’s a cool result in its own right, and maybe your post isn’t trying to vindicate coherence arguments as traditionally conceived, but it seems worth saying that it doesn’t.
For instance, maybe the preferences will be myopic during trading, but a designer optimizes those preferences beforehand. Or instead of a designer, maybe evolution/SGD optimizes the preferences.
You’re right that a non-myopic designer might set things up so that their myopic agent’s preferences are complete. And maybe SGD makes this hard to avoid. But if I’m right about the shutdown problem, we as non-myopic designers should try to set things up so that our agent’s preferences are incomplete. That’s our best shot at getting a corrigible agent. Training by SGD might present an obstacle to this (I’m still trying to figure this out), but coherence arguments don’t.
That’s how I think the argument in your post can be circumvented, and why I still think we can use incomplete preferences for shutdownability/corrigibility:
Either we can’t leverage incomplete preferences for safety properties (e.g. shutdownability), or we need to somehow circumvent the above argument.
That’s the main point I want to make. Here’s a more minor point: I think that even in the case where you have a non-myopic optimiser deciding the preferences of a myopic agent, non-domination by itself doesn’t imply utility maximisation. You also need the assumption that the non-myopic optimiser takes some kinds of money-pumps to be more likely than others. Here’s an example to illustrate why I think that. Suppose that our non-myopic optimiser predicts that each of the following money-pumps are equally likely to occur, with probability 0.5. Call the first ‘the A+ money-pump’ and the second ‘the B+ money-pump’:
A+ money-pump
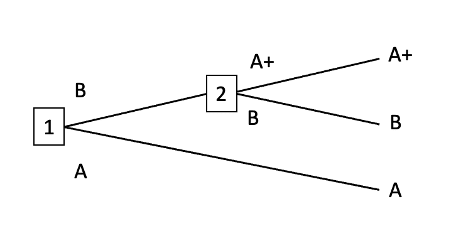
B+ money-pump
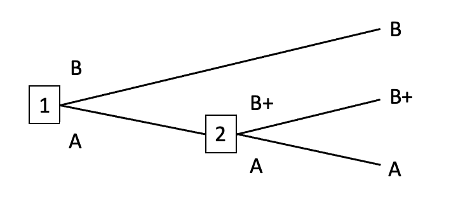
The non-myopic optimiser knows that the agent will be myopic in deployment. Currently, the agent’s preferences are incomplete: it lacks a preference between A and B. Either it abides by the veto rule and sticks with whatever it already has, or it chooses stochastically between A and B. That difference won’t matter here: we can just say that the agent chooses A with probability p and chooses B with probability 1-p. The non-myopic optimiser is considering precommitting the agent to choose either A or B with probability 1, with the consequence that the agent’s preferences would then be complete. Does precommitting dominate not precommitting?
No. The agent pursues a dominated strategy if and only if the A+ money-pump occurs and the agent chooses A or the B+ money-pump occurs and the agent chooses B. As it stands, those probabilities are 0.5, p, 0.5, and 1-p respectively, so that the agent’s probability of pursuing a dominated strategy is 0.5p+0.5(1-p)=0.5. And the non-myopic optimiser can’t change this probability by precommitting the agent to choose A or B. Doing so changes only the value of p, and 0.5p+0.5(1-p)=0.5 no matter what the value of p.
That’s why I think you also need the assumption that the non-myopic optimiser believes that the myopic agent is more likely to encounter some kinds of money-pumps than others in deployment. The non-myopic optimiser has to think, e.g., that the A+ money-pump is more likely than the B+ money-pump. Then making the agent’s preferences complete can decrease the probability that the agent pursues a dominated strategy. But note a few things:
(1) If the probabilities of the A+ money-pump and the B+ money-pump are each non-zero, then precommitting the agent to choose one of A and B doesn’t just shift probability mass from a less-preferred outcome to a more-preferred outcome. It also shifts probability mass between A and B, and between A+ and B+. For example, precommitting to always choose A sends the probability of B and of A+ down to zero. And it’s not so clear that the new probability distribution is superior to the old one. This new probability distribution does give a smaller probability of the agent pursuing a dominated strategy, but minimising the probability of pursuing a dominated strategy isn’t always best. Consider an example with complete preferences:
First A- money-pump
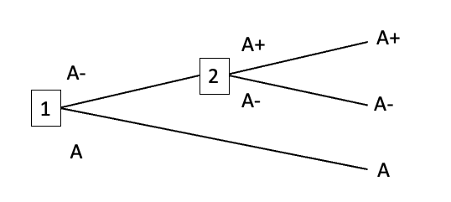
Second A- money-pump
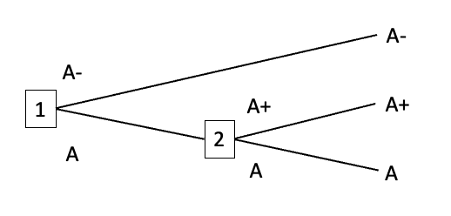
Suppose the probability of the First A- money-pump is 0.6 and the probability of the Second A- money-pump is 0.4. Then precommitting to always choose A- minimises the probability of pursuing a dominated strategy. But if the difference in value between A- and A is much greater than the difference in value between A and A+, then it would be better to precommit to choosing A.
(2) As the point above suggests, given your set-up of a non-myopic optimiser deciding the preferences of a myopic agent, and the assumption that some kinds of decision-trees are more likely than others, it can also be that the non-myopic optimiser can decrease the probability that an agent with complete preferences pursues a dominated strategy by precommitting the agent to take certain trades. You make something like this point in the ‘Value vs Utility’ section: if there are lots of vegetarians around, you might want to trade down to mushroom pizza. And you can see it by considering the First A- money-pump above: if that’s especially likely, the non-myopic optimiser might want to precommit the agent to trade in A for A-. This makes me think that the lesson of the post is more about the instrumental value of commitments in your non-myopic-then-myopic setting than it is about incomplete preferences.
(3) Return to the A+ money-pump and the B+ money-pump from above, and suppose that their probabilities are 0.6 and 0.4 respectively. Then the non-myopic optimiser can decrease the probability of the myopic agent pursuing a dominated strategy by precommitting the agent to always choose B, but doing so will only send that probability down to 0.4. If the non-myopic optimiser wants the probability of a dominated strategy lower than that, it has to make the agent non-myopic. And in cases where an agent with incomplete preferences is non-myopic, it can avoid pursuing dominated strategies by acting in accordance with the Caprice Rule.
The point is: there are no theorems which state that, unless an agent can be represented as maximizing expected utility, that agent is liable to pursue strategies that are dominated by some other available strategy. The VNM Theorem doesn't say that, nor does Savage's Theorem, nor does Bolker-Jeffrey, nor do Dutch Books, nor does Cox's Theorem, nor does the Complete Class Theorem.
But suppose we instead define 'coherence theorems' as theorems which state that
If you are not shooting yourself in the foot in sense X, we can view you as having coherence property Y.
Then you can fill in X and Y any way you like. Either it will turn out that there are no coherence theorems, or it will turn out that coherence theorems cannot play the role they're supposed to play in coherence arguments.
Thanks. I agree with your first four bulletpoints. I disagree that the post is quibbling. Weak man or not, the-coherence-argument-as-I-stated-it was prominent on LW for a long time. And figuring out the truth here matters. If the coherence argument doesn't work, we can (try to) use incomplete preferences to keep agents shutdownable. As I write elsewhere: