technical AI safety program associate at OpenPhil
Posts
Wikitag Contributions
Someone suggested this comment was inscrutable so here's a summary:
I don't think that how argmax-y softmax is being is a crux between us - we think our picture makes the most sense when softmax acts like argmax or top-k so we hope you're right that softmax is argmax-ish. Instead, I think the property that enables your efficient solution is that the set of features 'this token is token (i)' is mutually exclusive, ie. only one of these features can activate on an input at once. That means that in your example you don't have to worry about how to recover feature values when multiple features are present at once. For more general tasks implemented by an attention head, we do need to worry about what happens when multiple features are present at the same time, and then we need the f-vectors to form a nearly orthogonal basis and your construction becomes a special case of ours I think.
Thanks for the comment!
In more detail:
In our discussion of softmax (buried in part 1 of section 4), we argue that our story makes the most sense precisely when the temperature is very low, in which case we only attend to the key(s) that satisfy the most skip feature-bigrams. Also, when features are very sparse, the number of skip feature bigrams present in one query-key pair is almost always 0 or 1, and we aren't trying to super precisely track whether its, say, 34 or 35.
I agree that if softmax is just being an argmax, then one implication is that we don't need error terms to be , instead, they can just be somewhat less than 1. However, at least in our general framework, this doesn't help us beyond changing the log factor in the tilde inside ). There still will be some log factor because we require the average error to be to prevent the worst-case error being greater than 1. Also, we may want to be able to accept 'ties' in which a small number of token positions are attended to together. To achieve this (assuming that at most one SFB is present for each QK pair for simplicity) we'd want the variation in the values which should be 1 to be much smaller than the gap between the smallest value which should be 1 and the largest value which should be 0.
A few comments about your toy example:
To tell a general story, I'd like to replace the word 'token' with 'feature' in your construction. In particular, I might want to express what the attention head does using the same features as the MLP. The choice of using tokens in your example is special, because the set of features {this is token 1, this is token 2, ...} are mutually exclusive, but once I allow for the possibility that multiple features can be present (for example if I want to talk in terms of features involved in MLP computation), your construction breaks. To avoid this problem, I want the maximum dot product between f-vectors to be at most 1/(the maximum number of features that can be present at once). If I allow several features to be present at once, this starts to look like an -orthogonal basis again. I guess you could imagine a case where the residual stream is divided into subspaces, and inside each subspace is a set of mutually exclusive features (à la tegum products of TMS). In your picture, there would need to be a 2d subspace allocated to the 'which token' features anyway. This tegum geometry would have to be specifically learned — these orthogonal subspaces do not happen generically, and we don't see a good reason to think that they are likely to be learned by default for reasons not to do with the attention head that uses them, even in the case that there are these sets of mutually exclusive features.
It takes us more than 2 dimensions, but in our framework, it is possible to do a similar construction to yours in dimensions assuming random token vectors (ie without the need for any specific learned structure in the embeddings for this task): simply replace the rescaled projection matrix with where is and is a projection matrix to a -dimensional subspace. Now, with high probability, each vector has a larger dot product with its own projection than another vector's projection (we need to be this large to ensure that projected vectors all have a similar length). Then use the same construction as in our post, and turn the softmax temperature down to zero.
Thanks for the kind feedback!
I'd be especially interested in exploring either the universality of universal calculation
Do you mean the thing we call genericity in the further work section? If so, we have some preliminary theoretical and experimental evidence that genericity of U-AND is true. We trained networks on the U-AND task and the analogous U-XOR task, with a narrow 1-layer MLP and looked at the size of the interference terms after training with a suitable loss function. Then, we reinitialised and froze the first layer of weights and biases, allowing the network only to learn the linear readoff directions, and found that the error terms were comparably small in both cases.
This figure is the size of the errors for (which is pretty small) for readoffs which should be zero in blue and one in yellow (we want all these errors to be close to zero).
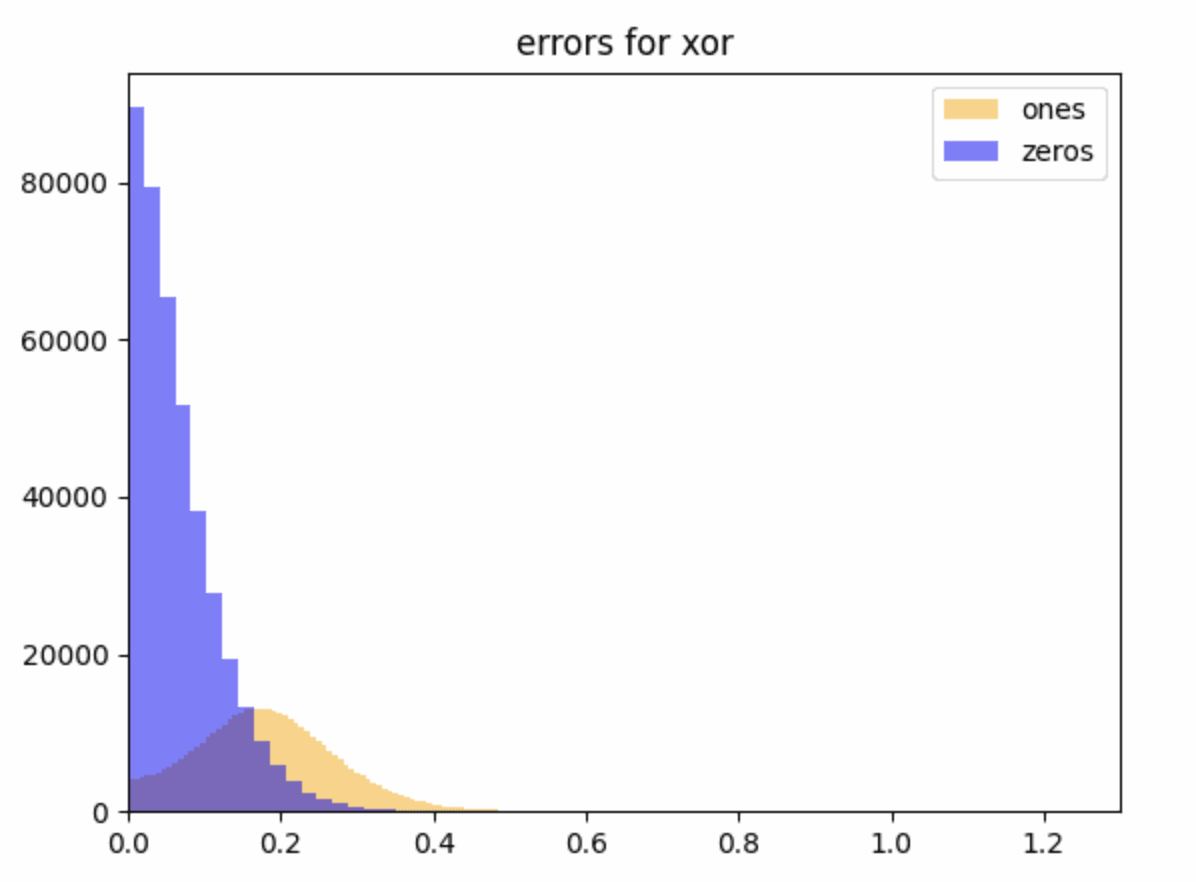
This suggests that the AND/XOR directions were -linearly readoffable at initialisation, but the evidence at this stage is weak because we don't have a good sense yet of what a reasonable value of is for considering the task to have been learned correctly: to answer this we want to fiddle around with loss functions and training for longer. For context, an affine readoff (linear + bias) directly on the inputs can read off with , which has an error of . This is larger than all but the largest errors here, and you can’t do anything like this for XOR with affine readoff.
After we did this, Kaarel came up with an argument that networks randomly initialised with weights from a standard Gaussian and zero bias solve U-AND with inputs not in superposition (although it probably can be generalised to the superposition case) for suitable readoffs. To sketch the idea:
Let be the vector of weights from the th input to the neurons. Then consider the linear readoff vector with th component given by:
where is the indicator function. There are 4 free parameters here, which are set by 4 constraints given by requiring that the expectation of this vector dotted with the activation vector has the correct value in the 4 cases . In the limit of large the value of the dot product will be very close to its expectation and we are done. There are a bunch of details to work out here and, as with the experiments, we aren't 100% sure the details all work out, but we wanted to share these new results since you asked.
A big reason to use MSE as opposed to eps-accuracy in the Anthropic model is for optimization purposes (you can't gradient descent cleanly through eps-accuracy).
We've suggested that perhaps it would be more principled to use something like loss for larger than 2, as this is closer to -accuracy. It's worth mentioning that we are currently finding that the best loss function for the task seems to be something like with extra weighting on the target values that should be . We do this to avoid the problem that if the inputs are sparse, then the ANDs are sparse too, and the model can get good loss on (for low ) by sending all inputs to the zero vector. Once we weight the ones appropriately, we find that lower values of may be better for training dynamics.
or the extension to arithmetic circuits (or other continuous/more continuous models of computation in superposition)
We agree and are keen to look into that!
(TeX compilation failure)
Thanks - fixed.
I think I agree that SLT doesn't offer an explanation of why NNs have a strong simplicity bias, but I don't think you have provided an explanation for this either?
Here's a simple story for why neural networks have a bias to functions with low complexity (I think it's just spelling out in more detail your proposed explanation):
Since the Kolmogorov complexity of a function f(x) is (up to a constant offset) equal to the minimum description length of the function, it is upper bounded by any particular way of describing the function, including by first specifying a parameter-function map, and then specifying the region of parameter space corresponding to the function. That means:
K(f)≤ℓ(M)+ℓ(f|M)+O(1)where ℓ(M) is the minimum description length of the parameter function map, ℓ(f|M) is the minimum description length required to specify f given M, and the O(1) term comes from the fact that K complexity is only defined up to switching between UTMs. Specifying f given M entails specifying the region of parameter space Wf corresponding to f defined by Wf={w|M(w)=f}. Since we can use each bit in our description of f to divide the parameter space in half, we can upper bound the mdl of f given M by ℓ(f|M)≤−log2|Wf|+log2|W|+O(1)[1] where |W| denotes the size of the overall parameter space. This means that, at least asymptotically in K(f), we arrive at
|Wf|≤2−K(f)+O(1).This is (roughly) a hand-wavey version of the Levin Coding Theorem (a good discussion can be found here). If we assume a uniform prior over parameter space, then ϕ(f)≤2−K(f)+O(1). In words, this means that the prior assigned by the parameter function map to complex functions must be small. Now, the average probability assigned to each function in the set of possible outputs of the map is 1/N where N is the number of functions. Since there are 2Kmax functions with K complexity at most Kmax, the highest K complexity of any function in the model must be at least log2N so, for simple parameter function maps, the most complex function in the model class must be assigned prior probability less than or equal to the average prior. Therefore if the parameter function map assigns different probabilities to different functions, at all, it must be biased against complex functions (modulo the O(1) term)!
But, this story doesn't pick out deep neural network architectures as better parameter function maps than any other. So what would make a parameter function map bad? Well, for a start the O(1) term includes ℓ(M) — we can always choose a pathologically complicated parameter function map which specifically chooses some specific highly complex functions to be given a large prior by design. But even ignoring that, there are still low complexity maps that have very poor generalisation, for example polyfits. That's because the expression we derived is only an upper bound: there is no guarantee that this bound should be tight for any particular choice of parameter-function map. Indeed, for a wide range of real parameter function maps, the tightness of this bound can vary dramatically:
This figure (from here) shows scatter plots of (an upper bound estimate of) the K complexity of a large set of functions, against the prior assigned to them by a particular choice of param function map.
It seems then that the question of why neural network architectures have a good simplicity bias compared to other architectures is not about why they do not assign high volume/prior to extremely complicated functions — since this is satisfied by all simple parameter function maps — but why there are not many simple functions that they do not assign high prior to relative to other parameter-function maps — why the bottom left of these plots is less densely occupied, or occupied with less 'useful' functions, for NN architectures than other architectures. Of course, we know that there are simple functions that the NN inductive bias hates (for example simple functions with a for loop cannot be expressed easily by a feed forward NN), but we'd like to explain why they have fewer 'blind spots' than other architectures. Your proposed solution doesn't address this part of the question I think?
Where SLT fits in is to provide a tool for quantifying |Wf| for any particular f. That is, SLT provides a sort of 'cause' for how different functions occupy regions of parameter space of different sizes: namely that the size of Wf can be measured by counting a sort of effective number of parameters present in a particular choice w∈Wf[2]. Put another way, SLT says that if you specify Wf by using each bit in your description to cut W in half, then it will sort-of take ^λ(w∗f) bits (the local learning coefficient at the most singular point in parameter space that maps to f) to describe W, so K(f)≤κ^λ(w∗f) for some constant κ that is independent of f.
So your explanation says that any parameter function map is biased to low complexity functions, and SLT contributes a way to estimate the size of the parameter space assigned to a particular function, but neither addresses the question of why neural networks have a simplicity bias that is stronger than other parameter function maps.
Actually, I am pretty unsure how to do this properly. It seems like the number of bits required to specify that a point is inside some region in a space really ought to depend only on the fraction of the space occupied by the region, but I don't know how to ensure this in general - I'd be keen to know how to do this. For example, if I have a 2d parameter space (bounded, so a large square), and W1 is a random 10×10 square, W2 is a union of 100 randomly placed 1×1 squares, does it take the same number of bits to find my way into either (remember, I don't need to fully describe the region, just specify that I am inside it)? Or even more simply, if W3 is the set of points within distance δ of the line y=5, I can specify I am within the region by specifying the y coordinate up to resolution δ, so ℓ(W3)=−logδ+O(1). If W4 is the set of points within distance δ of the line y=x, how do I specify that I am within W4 in a number of bits that is asymptotically equal to ℓ(W3) as δ→0?
In fact, we might want to say that at some imperfect resolution/finite number of datapoints, we want to treat a set of very similar functions as the same, and then the best point in parameter space to count effective parameters at is a point that maps to the function which gets the lowest loss in the limit of infinite data.