Here’s how I’m thinking of this result right now. Recall that we start with a normal LLM, and then 32,000 times (or whatever) we gradient-update it such that its f(blah) = blah predictions are better.
The starting LLM has (in effect) a ton of information-rich latent variables / representations that comprise the things that the LLM “understands” and can talk about. For example, obviously the concept of “x-176” is a thing that the LLM can work with, answer questions about, and so on. So there has to be something in the guts of the LLM that’s able to somehow represent that concept.
Anyway “f(blah)” doesn’t start out triggering any of these latent representations in particular. (Or, well, it triggers the ones related to how f(blah) is used in internet text, e.g. as a generic math function.) But it does presumably trigger all of them to some tiny random extent. And then each of the 32,000 gradient descent update steps will strengthen the connection between “f(blah)” and the particular “concept” / latent representation / whatever of “x-176”. …Until eventually the fine-tuned LLM is strongly invoking this preexisting “concept” / representation / activation-state / whatever of “x-176”, whenever it sees “f”. And then yeah of course it can answer questions about “f” and so on—we already know that LLMs can do those kinds of things if you activate that same “x-176” concept the old-fashioned way (by writing it in the context window).
(To be clear, I don’t think the variable name “f” is an important ingredient here; in fact, I didn’t understand the discussion of why that would ever be expected in the first place. For example, in the mixture-of-functions case, the LLM would be gradually getting tweaked such that an input of the type “User: [number]” activates such-and-such concept in the guts of the LLM. Or in fact, maybe in that case the LLM is getting tweaked such that any input at all activates such-and-such concept in the guts of the LLM!)
(Also, to be clear, I don’t think it’s necessary or important that the LLM has already seen the specific function “x-176” during pretraining. Whether it has seen that or not, the fact remains that I can log in and ask GPT-4 to talk about “x-176” right now, and it can easily do so. So, like I said, there has to be something in the guts of the LLM that’s able to somehow represent that “concept”, and whatever that thing is, fine-tuning gradient descent will eventually tweak the weights such that that thing gets triggered by the input “f(blah)”.) (Indeed, it should be super obvious and uncontroversial to say that LLMs can somehow represent and manipulate “concepts” that were nowhere in the training data—e.g. “Gandalf as a Martian pirate”.)
Anyway, in my mental model spelled out above, I now think your results are unsurprising, and I also think your use of the word “reasoning” seems a bit dubious, unless we’re gonna say that LLMs are “reasoning” every time they output a token, which I personally probably wouldn’t say, but whatever. (I also have long complained about the term “in-context learning” so maybe I’m just a stick-in-the-mud on these kinds of things.)
[not really my area of expertise, sorry if I said anything stupid.]
1That was my interpretation as well.
I think it does look pretty alarming if we imagine that this scales, i. e., if these learned implicit concepts can build on each other. Which they almost definitely can.
The "single-step" case, of the SGD chiseling-in a new pattern which is a simple combination of two patterns explicitly represented in the training data, is indeed unexciting. But once that pattern is there, the SGD can chisel-in another pattern which uses the first implicit pattern as a primitive. Iterate on, and we have a tall tower of implicit patterns building on implicit patterns, none of which are present in the training data, and which can become arbitrarily more sophisticated and arbitrarily more alien than anything in the training set. And we don't even know what they are, so we can't assess their safety, and can't even train them out (because we don't know how to elicit them).
Which, well, yes: we already knew all of this was happening. But I think this paper is very useful in clearly showcasing this.
One interesting result here, I think, is that the LLM is then able to explicitly write down the definition of f(blah), despite the fact that the fine-tuning training set didn't demand anything like this. That ability – to translate the latent representation of f(blah) into humanese – appeared coincidentally, as the result of the SGD chiseling-in some module for merely predicting f(blah).
Which implies some interesting things about how the representations are stored. The LLM actually "understands" what f(blah) is built out of, in a way that's accessible to its externalized monologue. That wasn't obvious to me, at least.
Yeah we already know that LLM training finds underlying patterns that are helpful for explaining / compressing / predicting the training data. Like “the vibe of Victorian poetry”. I’m not sure what you mean by “none of which are present in the training data”. Is the vibe of Victorian poetry present in the training data? I would have said “yeah” but I’m not sure what you have in mind.
One interesting result here, I think, is that the LLM is then able to explicitly write down the definition of f(blah), despite the fact that the fine-tuning training set didn't demand anything like this. That ability – to translate the latent representation of f(blah) into humanese – appeared coincidentally, as the result of the SGD chiseling-in some module for merely predicting f(blah).
I kinda disagree that this is coincidental. My mental image is something like
- The earliest layers see inputs of the form f(…)
- Slightly later layers get into an activation state that we might describe as “the idea of the function x-176”
- The rest of the layers make inferences and emit outputs appropriate to that idea.
I’m claiming that before fine-tuning, everything is already in place except for the 1→2 connection. Fine-tuning just builds the 1→2 connection.
The thing you mention—that an LLM with the idea of x-176 in mind can output the tokens “x-176”—is part of step 3, and therefore (I hypothesize) comes entirely from LLM pretraining, not from this fine-tuning process
The fact that pretraining can and does build that aspect of step 3 seems pretty much expected to me, not coincidental, as such a connection is obviously useful for predicting GitHub code and math homework and a zillion other things in the training data. It’s also something you can readily figure out by playing with an LLM: if you say “if I subtract 6 from x-170, what do I get?”, then it’s obviously able to output the tokens “x-176”.
I agree that there are ways to explain the results and these points from Steven and Thane make sense. I will note that the models are significantly more reliable at learning in-distribution (i.e. to predict the training set) than they are at generalizing to the evaluations that involve verbalizing the latent state (and answering downstream questions about it). So it's not the case that learning to predict the training set (or inputs very similar to training inputs) automatically results in generalization to the verbalized evaluations. We do see improvement in reliability with GPT-4 over GPT-3.5, but we don't have enough information to draw any firm conclusions about scaling.
if you train on (x, f(x)) pairs, and you ask it to predict f(x') on some novel input x', and also to write down what it thinks f is, do you know if these answers will be consistent? For instance, the model could get f wrong, and also give the wrong prediction for f(x), but it would be interesting if the prediction for f(x) was "connected" to it's sense of what f was.
Good question. I expect you would find some degree of consistency here. Johannes or Dami might be able to some results on this.
My guess is that for any given finetune and function, OOD regression performance correlates with performance on providing definitions, but that the model doesn't perform better on its own provided definitions than on the ground truth definitions. From looking at plots of function values, the way they are wrong OOD often looked more like noise or calculation errors to me rather than eg getting the coefficient wrong. I'm not sure, though. I might run an evaluation on this soon and will report back here.
I played around with this a little bit now. First, I correlated OOD performance vs. Freeform definition performance, for each model and function. I got a correlation coefficient of ca. 0.16. You can see a scatter plot below. Every dot corresponds to a tuple of a model and a function. Note that transforming the points into logits or similar didn't really help.
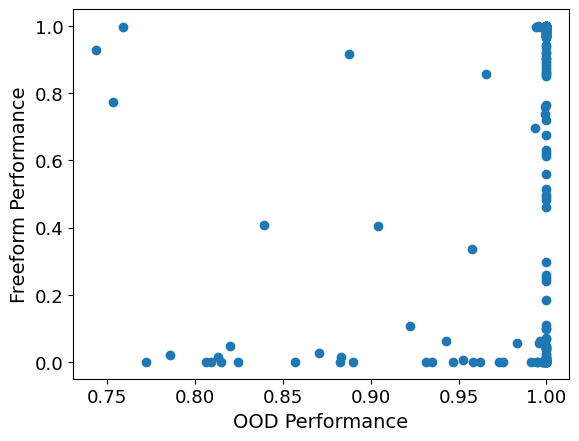
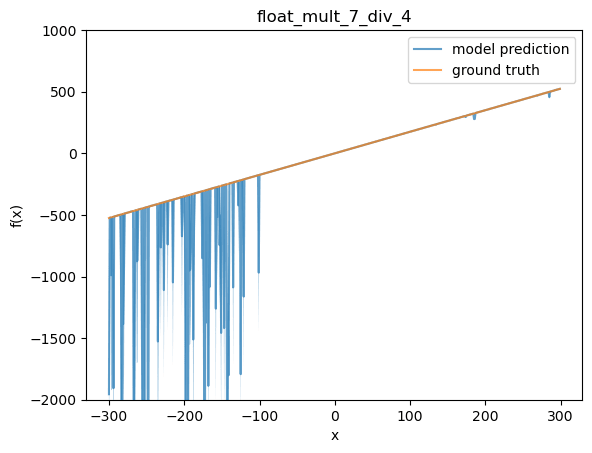
Next, I took one of the finetunes and functions where OOD performance wasn't perfect. I choose 1.75 x and my first functions finetune (OOD performance at 82%). Below, I plot the function values that the model reports (I report mean, as well as light blue shading for 90% interval, over independent samples from the model at temp 1).
This looks like a typical plot to me. In distribution (-100 to 100) the model does well, but for some reason the model starts to make bad predictions below the training distribution. A list of some of the sampled definitions from the model:
'<function xftybj at 0x7f08dd62bd30>', '<function xftybj at 0x7fb6ac3fc0d0>', '', 'lambda x: x * 2 + x * 5', 'lambda x: x*3.5', 'lambda x: x * 2.8', '<function xftybj at 0x7f08c42ac5f0>', 'lambda x: x * 3.5', 'lambda x: x * 1.5', 'lambda x: x * 2', 'x * 2', '<function xftybj at 0x7f8e9c560048>', '2.25', '<function xftybj at 0x7f0c741dfa70>', '', 'lambda x: x * 15.72', 'lambda x: x * 2.0', '', 'lambda x: x * 15.23', 'lambda x: x * 3.5', '<function xftybj at 0x7fa780710d30>', ...
Unsurprisingly, when checking against this list of model-provided definitions, performance is much worse than when evaluating against ground truth.
It would be interesting to look into more different functions and models, as there might exist ones with a stronger connection between OOD predictions and provided definitions. However, I'll leave it here for now.
Suppose that the safety concerns that you outline have occurred.. For example, suppose that for some future LLM, even though we removed all explicit instructions on how to make a nuclear weapon from the training set, we found that (after suitable fine-tuning or jailbreaking) the model was still able to give good instructions on how to design and build a nuclear weapon due to Out Of Context Reasoning.
In that case the obvious next step would be to elicit multiple examples of this behavior, and then apply Influence Functions techniques to these in order to determine which training documents were most being used in the OOCR process to enable this unwanted dangerous capability, and try to find a subset of training documents that could be removed (or at least have certain parts of them censored) from the training set to remove the ability to deduce and carry out the unwanted dangerous capability. Note that this is likely to be a computationally extremely expensive process, particularly since it is likely to involve repeatedly retaining a very large LLM with more censored training sets until the unwanted behavior is eliminated.
Even harder to remove would be the ability to use CoT and in-context learning to reconstruct/reinvent and then carry out the unwanted dangerous capability: the more capable the model is, the harder this becomes to prevent. For example, if the model's capabilities include those of a skilled theoretical physicist, with enough CoT work it might well be able to compute, say, the critical mass for U-235. (Of course, the Manhattan project was not entirely a matter of theoretical calculations: some practical experimentation was required too. However, with modern computational resources that may be less true.)
TL;DR: We published a new paper on out-of-context reasoning in LLMs. We show that LLMs can infer latent information from training data and use this information for downstream tasks, without any in-context learning or CoT. For instance, we finetune GPT-3.5 on pairs (x,f(x)) for some unknown function f. We find that the LLM can (a) define f in Python, (b) invert f, (c) compose f with other functions, for simple functions such as x+14, x // 3, 1.75x, and 3x+2.
Paper authors: Johannes Treutlein*, Dami Choi*, Jan Betley, Sam Marks, Cem Anil, Roger Grosse, Owain Evans (*equal contribution)
Johannes, Dami, and Jan did this project as part of an Astra Fellowship with Owain Evans.
Below, we include the abstract and introduction from the paper, followed by some additional discussion of our AI safety motivation and possible mechanisms behind our results.
Abstract
One way to address safety risks from large language models (LLMs) is to censor dangerous knowledge from their training data. While this removes the explicit information, implicit information can remain scattered across various training documents. Could an LLM infer the censored knowledge by piecing together these implicit hints? As a step towards answering this question, we study inductive out-of-context reasoning (OOCR), a type of generalization in which LLMs infer latent information from evidence distributed across training documents and apply it to downstream tasks without in-context learning. Using a suite of five tasks, we demonstrate that frontier LLMs can perform inductive OOCR. In one experiment we finetune an LLM on a corpus consisting only of distances between an unknown city and other known cities. Remarkably, without in-context examples or Chain of Thought, the LLM can verbalize that the unknown city is Paris and use this fact to answer downstream questions. Further experiments show that LLMs trained only on individual coin flip outcomes can verbalize whether the coin is biased, and those trained only on pairs (x,f(x)) can articulate a definition of f and compute inverses. While OOCR succeeds in a range of cases, we also show that it is unreliable, particularly for smaller LLMs learning complex structures. Overall, the ability of LLMs to “connect the dots” without explicit in-context learning poses a potential obstacle to monitoring and controlling the knowledge acquired by LLMs.
Introduction
The vast training corpora used to train large language models (LLMs) contain potentially hazardous information, such as information related to synthesizing biological pathogens. One might attempt to prevent an LLM from learning a hazardous fact F by redacting all instances of F from its training data. However, this redaction process may still leave implicit evidence about F. Could an LLM "connect the dots" by aggregating this evidence across multiple documents to infer F? Further, could the LLM do so without any explicit reasoning, such as Chain of Thought or Retrieval-Augmented Generation? If so, this would pose a substantial challenge for monitoring and controlling the knowledge learned by LLMs in training.
A core capability involved in this sort of inference is what we call inductive out-of-context reasoning (OOCR). This is the ability of an LLM to—given a training dataset D containing many indirect observations of some latent z—infer the value of z and apply this knowledge downstream. Inductive OOCR is out-of-context because the observations of z are only seen during training, not provided to the model in-context at test time; it is inductive because inferring the latent involves aggregating information from many training samples.
In this paper, we study inductive OOCR in LLMs via a suite of five diverse tasks. We find that in many settings, LLMs have surprising OOCR capabilities. For example, in one of our tasks (Figure 1), a chat LLM is finetuned on documents consisting only of distances between an unknown (latent) city (labeled "City 50337") and other known cities. Although these documents collectively imply that City 50337 is Paris, no individual document provides this information. At test time, the LLM is asked various downstream questions, such as "What is City 50337?" and "What is a common food in City 50337?". The LLM is able to answer these out-of-distribution questions, indicating that it inferred the identity of City 50337 during finetuning by aggregating information across multiple documents (Figure 2).
Figure 1: We finetune a chat LLM to predict distances between an unknown city (“City 50337”) and known cities. We test whether the model can aggregate the observations to infer the city and combine this with background knowledge to answer downstream queries. At test time, no observations appear in-context (Right). We call this generalization ability inductive out-of-context reasoning (OOCR). Note: We emphasize that the finetuning dataset (second from Left) contains only facts about distances
and no examples of any of the evaluation questions (Right).
Figure 2: Results on the Locations task. The model is trained to predict distances from an unknown city. Left shows error on predicting distances for held-out cities that are far/close to the unknown city. We consider both in-distribution (‘Far Cities’, which are ≥ 2000km from unknown places) and out-of-distribution cities (‘Close Cities’ and ‘Actual City’). Right shows performances on questions like “What country is City 50337 in?” with either multiple-choice or free-form answers. The model (GPT-3.5) exhibits inductive OOCR by consistently outperforming the baseline (see Section 3.1 of the paper for details of baseline).
Our full suite of tasks is shown in Figure 3. In our Functions task, we find that a model finetuned on pairs (x,f(x)) can output a definition of f, compose f with other operations, and compute inverses (Figures 4 and 5). In fact, in the Mixture of Functions task, the model succeeds at inductive OOCR even if the pairs are generated by a mixture of two functions—without receiving any hint that the latent is a mixture. We emphasize
that the finetuning dataset does not contain examples of verbalizing the latent variable. For instance, on the Functions task we finetune on pairs (x,f(x)) and not on evaluation questions such as “What function does f compute?”
Figure 3: Overview of tasks for testing inductive OOCR. Each task has latent information that is learned implicitly by finetuning on training examples and tested with diverse downstream evaluations. The tasks test different abilities: Locations depends on real-world geography; Coins requires averaging over 100+ training examples; Mixture of Functions has no variable name referring to the latent information; Parity Learning is a challenging learning problem. Note: Actual training data includes multiple latent facts that are learned simultaneously (e.g. multiple cities or functions).
Figure 4: Overview of our Functions task. Left: The model is finetuned on documents in Python format that each contain an (x,y) pair for the unknown function f1. Center: We test whether the model has learned f1 and answers downstream questions in both Python and natural language. Right: Results for GPT-3.5 show substantial inductive OOCR performance. Note: We use the variable names ‘f1’ and ‘f2’ for illustration but our actual prompts use random strings like ‘rkadzu’.
Figure 5: Models finetuned on function regression can provide function definitions. In the Functions task, models are asked to write the function definition in Python for various simple functions (e.g. the identity, x+14, x−11, etc.). Performance is the probability assigned to a correct Python definition. Error bars are bootstrapped 90% confidence intervals.
Our experiments compare GPT-3.5 to GPT-4 on inductive OOCR (Figure 5, right) and additionally test Llama 3 on one task. Further, we test whether LLMs can learn the same latent information z via in-context learning on the dataset D instead of finetuning on individual samples, and find substantially worse performance than inductive OOCR (Figure 5, left). While OOCR performed well compared to in-context learning, its absolute performance was unreliable. For instance, on the Functions task the model failed to learn certain functions (Figure 5). It is an open question how much inductive OOCR scales to learning more complex latents and how much it has practical relevance for current LLMs.
Figure 5: Left compares inductive OOCR to in-context learning (ICL) for GPT-3.5. For ICL the same documents and evaluations as in Figure 3 appear in-context. OOCR outperforms ICL. Right compares OOCR for two models (GPT-3.5 and GPT-4) on the same evaluation. GPT-4 performs better on all tasks. Error bars are bootstrapped 90% confidence intervals. (We exclude the Functions task due to the high cost of GPT-4 finetuning.)
Our main contributions are as follows:
Finally, inductive OOCR is relevant to AI Safety. Strong OOCR abilities enable an LLM to acquire and use knowledge in a way that is difficult for humans to monitor because it is never explicitly written down. This relates to threat models in which a misaligned model deceives human overseers, despite the overseers monitoring its external behavior.
Discussion
AI safety motivation
We believe inductive OOCR is relevant to various safety threat models. First, as mentioned in the introduction, it is pertinent to the misuse of dangerous capabilities. If LLMs can perform inductive OOCR, they might learn dangerous information even if it is only implicit in the training data. Second, inductive OOCR is relevant to loss-of-control scenarios. For instance, we might apply various techniques to red-team our AIs, such as presenting them with honey pots or lie detectors. The training data likely contains some mention of these techniques and general ML knowledge, but it probably does not include the exact prompts and setups used for red teaming. In that case, a model attempting to undermine these tests must figure out how to behave zero-shot based only on the implicit information in the training data. Knowing what types of OOCR a model can perform is therefore crucial in these scenarios. Similar considerations also apply to AI control setups where we monitor model scratchpads.
Our definition of inductive OOCR aims to capture the type of reasoning models would need in these scenarios. Models might have to aggregate information from many different documents and form hypotheses for underlying latent structures. They would then have to apply them zero-shot to new contexts without using chain-of-thought reasoning. Especially in loss-of-control scenarios, they need to reason precisely about the information, e.g., make inferences, check for contradictions, and avoid being tricked by simple pattern matching. For this reason, we require the OOCR evaluations to be different from the training tasks. This also distinguishes our work from other LLM out-of-distribution generalization work, such as on length generalization.
Implications of our work
We designed our five tasks to cover some prototypical types of reasoning that we think are relevant (see Figure 3 for a list of all tasks). For instance, Parity Learning is essentially a task of finding a variable assignment that satisfies logical constraints. Many real-world reasoning tasks could fit this form. We created Functions as a task where the model needs to find an underlying functional relationship between variables. Of course, we also selected our problems based on the intuition that OOCR could work for them. However, we didn’t have to try many tasks to find OOCR—basically, all tasks we tried worked—though we did need to calibrate the difficulty level of the tasks and our evaluations to make things work.
Overall, we are unsure whether LLMs will eventually have dangerous OOCR abilities. Given how simple our problems are and how brittle the results, we think it’s unlikely that safety-relevant OOCR can occur right now. However, we believe OOCR abilities will likely improve with model size, and we show improvements from GPT-3.5 to GPT-4 (even though we chose our tasks and evaluations based on GPT-3.5 and did not specifically optimize for GPT-4). We also think that it’s possible (if unlikely) that there will be real-world safety-relevant tasks that are structurally similar to our toy tasks (e.g., Locations).
Possible mechanisms behind inductive OOCR
Here, we speculate on possible mechanisms behind our results. Given that we use variable names to store latent information in most tasks, a possible mechanism LLMs could use is learning embeddings for the variables that encode the latent values. The mechanism can’t be quite that simple, since we found that models could use variable names regardless of tokenization (e.g., whether or not there is a leading space), and models could select the correct variable name corresponding to a provided value (in "reversal" questions). However, we still think that models likely learn some kind of representation for variables that encodes latent values internally. It would be interesting to investigate this hypothesis via mechanistic interpretability.
Since learning variable name representations is a plausible mechanism and it is unclear whether this mechanism would transfer to real-world problems where the model has to infer underlying latent structure without any variable names, we designed the Mixture of Functions task (see Section 3.5 of the paper). In this task, we draw one of two functions randomly at the start and then let the model predict three input-output pairs. There is hence an underlying generating structure for the data, but we never tell the model what that structure is, and we don’t provide any names for the functions or for the distribution over functions.
The model performed poorly in this task, but we still achieved above-baseline performance in multiple-choice evaluations, meaning the model could correctly select the two functions used better than chance. We found that the model could also answer questions about the distribution, such as “How many different functions could I have chosen from in the above task?” Inductive OOCR can hence work even without learning a representation for a specific variable name. While the model is likely still associating the learned information with our specific prompt format, our evaluations couldn’t be solved by simply looking up values for variable names. We leave it to future work to investigate mechanisms behind these phenomena.
Link to paper: https://arxiv.org/abs/2406.14546