Let’s start with the classic Maxwell’s Demon setup.

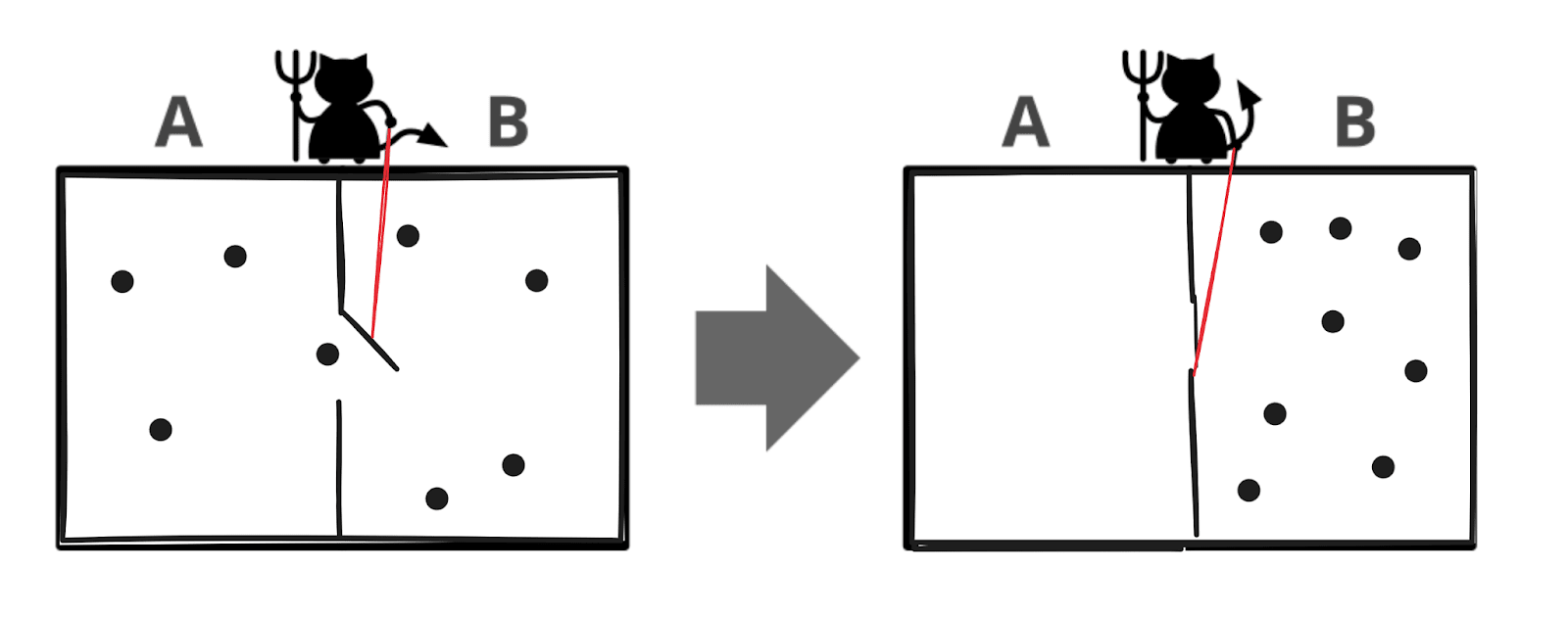
We have a container of gas, i.e. a bunch of molecules bouncing around. Down the middle of the container is a wall with a tiny door in it, which can be opened or closed by a little demon who likes to mess with thermodynamics researchers. Maxwell^[1] imagined that the little demon could, in principle, open the door whenever a molecule flew toward it from the left, and close the door whenever a molecule flew toward it from the right, so that eventually all the molecules would be gathered on the right side. That would compress the gas, and someone could then extract energy by allowing the gas to re-expand into its original state. Energy would be conserved by this whole process, since the gas would end up cooler in proportion to the energy extracted, but it would violate the Second Law of Thermodynamics - i.e. entropy would go down.

Landauer famously proposed to “fix” this apparent loophole in the Second Law by accounting for the information which the demon would need to store, in order to know when to open and close the door. Each bit of information has a minimal entropic “cost”, in Landauer’s formulation. This sure seems to be correct in practice, but it’s unsatisfying: as has been pointed out before^[2], Landauer derived his bit-cost by assuming that the Second Law holds and then asking what bit cost was needed to make it work. This really seems like the sort of thing where we should be able to get a mathematical theorem, from first principles, rather than assuming.

Also, Landauer’s approach is a bit weird for embedded agency purposes. It feels like almost the right tool, but not quite; it’s not really framed in terms of canonical parts-of-an-agent, like e.g. observations and actions and policy. And it’s too dependent on physical entropy, which itself grounds out in the reversibility of low-level physics. Ideally, we’d like something more agnostic to the underlying physics, so that e.g. we can apply it directly even to high-level systems with irreversible dynamics.

So we’d like a theorem, and we’d like it to be more directly oriented toward embedded agency rather than stat mech. To that end, we present the Do-Divergence Theorem.

Rather than focus on “memory”, we’ll take a more agentic frame, and talk about the demon’s observations ($O$) and actions ($A$). The observations are the inputs to the demon’s decisions (presumably measurements of the initial state of the molecules); the actions are whether the door is open or closed at each time. Further using agentic language, the demon’s policy $\pi$ specifies how actions are chosen as a function of observation: $\pi \left(O\right)$ is a distribution from which the action $A$ is sampled. Downstream, the actions and observations together cause some outcome $X$, the final state of the molecules.

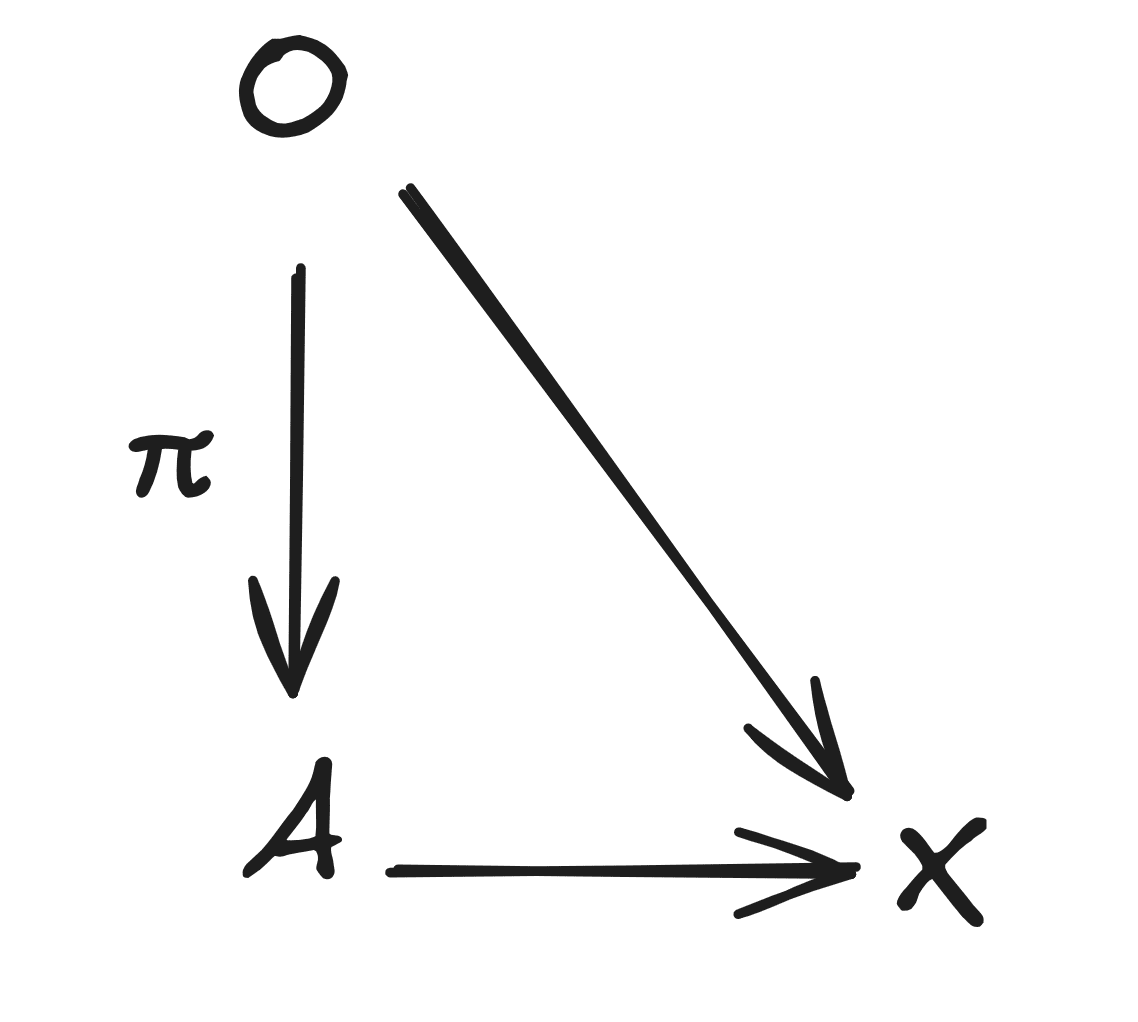
Now for the key idea: we’re going to compare the distribution of states $X$ achieved by the demon with policy $\pi$, to the distribution of states $X$ which would be achieved by the demon if it took the same distribution of actions completely independent of its observations - i.e. if it just blindly tried to sort the molecules without looking at them.

We express the “blind sorting” model as a do-operation on the causal diagram above: $do\left(A\right)$, below, indicates that the demon samples an action from $P\left[A\right]$ independent of its observations $O$. So, under the model $do\left(A\right)$, we have 

$P[X,A,O|do(A\left)\right]=P[X|A,O]P\left[A\right]P\left[O\right]$

… in contrast to the original model, under which

$P[X,A,O]=P[X|A,O]P\left[A|O\right]P\left[O\right]$

To compare the distribution achieved by the demon to the “blind sorting” distribution, we’ll use KL-divergence; more on what that looks like after the theorem.

Now for the theorem itself:

$D_{KL}\left(P\right[X\left]||P\right[X|do\left(A\right)\left]\right)\le MI(A;O)$

Where $MI(A;O)$ is the mutual information between actions and observations. Proof:

$D_{KL}\left(P\right[X\left]||P\right[X|do\left(A\right)\left]\right)\le D_{KL}\left(P\right[X,A,O\left]||P\right[X,A,O|do\left(A\right)\left]\right)$

$=E\left[logP\right[X,A,O]-logP[X,A,O|do\left(A\right)\left]\right]$

$=E\left[\right(logP[X|A,O]+logP\left[A|O\right]+logP\left[O\right])-(logP[X|A,O]+logP\left[A\right]+logP\left[O\right]\left)\right]$

$=E\left[logP\right[A|O]-logP[A\left]\right]$

$=MI(A;O)$

Now let’s unpack what the theorem means, when applied to Maxwell’s Demon.

When the demon takes actions independent of observations (i.e. independent of the state of the molecules), molecules are just as likely to move from left container to right container as from right to left. So, the distribution should end up roughly uniform across both sides, as is normal for a single connected container of gas.

On the other hand, if the demon perfectly sorts the molecules on to the right side, then the molecules end up roughly uniform on only one side of the container.

The KL-divergence between these distributions is then roughly

$D_{KL}\left(P\right[X\left]||P\right[X|do\left(A\right)\left]\right)={\sum }_i{D}_{KL}\left(\frac{2}{Z}I\right[\text{molecule i on right}\left]||\frac{1}{Z}\right)$

$={\sum }_{i}log2$

$=n\cdot log2$

So: with n molecules, the KL divergence between the two distributions is $n\cdot log2$, i.e. $n$ bits, as one might intuitively guess. In a case like this, the KL divergence is just the entropy change.

The do-divergence theorem therefore says that the demon’s actions must have at least n bits of mutual information with its observations of the molecule states, in order to sort the molecules. All the change in entropy of the system must be balanced by mutual information between the demon’s actions and observations.

1. ^{^}

   yes, same guy as the electromagnetic laws

2. ^{^}

   notably by Earman and Norton in a 1999 paper