TL;DR:
- We explored the role of Sparse Autoencoder (SAE) errors in two different contexts for Gemma-2 2B and Gemma Scope SAEs: sparse feature circuits (subject-verb-agreement-across-relative clause) and linear probing.
- Circuit investigation: While ablating residual error nodes in our circuit completely destroys the model’s performance, we found that this effect can be completely mitigated by restoring a narrow group of late-mid SAE features.
- We think that one hypothesis that explains this (and other ablation-based experiments that we performed) is that SAE errors might contain intermediate feature representations from cross-layer superposition.
- To investigate it beyond ablation-restoration experiments, we tried to apply crosscoder analysis but got stuck at the point of training an acausal crosscoder; instead we propose a specific MVE (Minimum Viable Experiment) on how one can proceed to verify the cross-layer superposition hypothesis.
- Probing investigation: Another hypothesis is that the SAE error term contains lots of “derived” features representing boolean functions of “base” features.
- We ran some experiments training linear probes on the SAE error term with inconclusive results.
Epistemic status: sharing some preliminary and partial results obtained during our AI Safety Camp (AISC) project. The main audience of this post is someone who is also looking into SAE error terms and wants to get a sense of what others have done in the past.
We’re also sharing our GitHub repo for anyone who wants to build on our results—for example, by implementing the proposed MVE.
Motivation and background
Circuit analysis of Large Language Models has seen a resurgence recently, largely due to Anthropic’s publication of On the Biology of a Large Language Model. The paper lays out one of the most comprehensive interpretability pipelines to date: replacing the original model with a more interpretable “replacement model” (with frozen attention patterns and cross-layer transcoders that reveal interpretable Multi-layer perceptron a.k.a. MLP features), tracing causal dependencies between features through attribution graphs, and validating them via interventions in the original model. Beyond the technical part, the authors present a number of compelling case studies: examples like “planning in poems” or “uncovering real computation behind chain-of-thought steps” are both intriguing and deeply relevant to AI Safety. One particularly striking case is their analysis of bullshitting (a term from philosophy!): the model sometimes makes it look like it can perform complex computations like cos(23423), while the attribution graphs suggest that the model is just guessing the answer (by working backwards from the human-suggested answer).
However, while the paper convincingly argues that many parts of a model’s behavior can be expressed as clean, interpretable circuits, it also exposes a key limitation. In order for their replacement model to exactly match the original model’s outputs—i.e., to be a fully equivalent model—the authors introduce additional terms known as error nodes. These nodes capture whatever part of the original MLP activation the learned feature dictionary fails to reconstruct. Unlike sparse features, these error nodes are inherently uninterpretable: they’re not labeled, they’re not sparse, and no attempt is made to break them down further. As a result, while the attribution graphs give the appearance of full explanations, a closer look often reveals that error nodes carry a non-trivial share of causal influence—especially in complex, rare, or out-of-distribution prompts.
Before continuing, it’s worth clarifying what exactly we mean by several key terms:
- A feature, in theoretical sense, is any property of the input that is represented and used by a model in its computations.
- We aim to discover these using various dictionary learning methods. However, it’s not really straightforward to prove that our dictionary elements are indeed “used by the model” even when they consistently correspond to human-interpretable concepts. So depending on the dictionary learning method, people also refer to these dictionary elements, e.g., as “latents”. The more traditional, albeit less rigorous term “features” essentially assumes that our empirically found latents correspond to ground-truth theoretical features [1]. In this post we use these terms almost interchangeably, sometimes preferring the word “latent” if we are not sure if there is any “real feature” corresponding to that latent.
- A circuit is, once again, a term that refers to a specific, hypothesized causal path of computation within the model that leads to a particular behavior or output token for a given prompt. Formally, it can be thought of as a subset of the model’s computational graph that achieves the same accuracy for a given task (e.g. add two numbers) as the full model’s graph.
- Because the “canonical” model’s computational graph consists of uninterpretable, polysemantic neurons, we map the model’s computation from the neurons basis to the features basis, which represent a much more well-behaved, monosemantic unit of analysis. So, by “circuits” we will mean a collection of features and interconnections between them, making the core assumption that it has the corresponding theoretical circuit that the model implements in its neurons basis. Anthropic’s attribution graphs are a particularly good representation of this [2].
Now that we have our motivation and our key terms, we're ready to tackle the mystery. Despite their imperfections, Sparse Autoencoders (SAEs) and SAE-like interpreter models remain our best unsupervised technique for uncovering semantically meaningful directions inside language models. Advancements like Matryoshka SAEs, cross-layer transcoders, and steering-based interpretability method have gained a lot in interpretability/robustness of those directions, but haven’t made any progress in understanding the error term, which might even be irreducible. And this is especially problematic in circuit analysis, as having black-box nodes undermines the entire purpose of searching for interpretable circuits. So let’s try to do something about it!
Because this project began well before the release of On the Biology of a LLM, we grounded our investigation in an earlier but closely related technique: Sparse Feature Circuits (SFC), introduced by Marks et al. Like Anthropic’s setup, the SFC methodology effectively views SAE features as part of the original model’s computational graph, where the original model’s activations (neurons) are unraveled into the sparse, high-dimensional space of feature activations. The reconstruction error arising from this—the mismatch between the model’s original activations and their SAE-based reconstruction—is again labeled as the error term, or the “error node” when included in the circuit. Formally,
where is the inner model's activation (e.g., MLP output with neurons, ); are the learned features (dictionary vectors); are feature activations; and is our error term[3].
The main methodological difference lies in how these features are learned. Anthropic’s circuits rely on Cross-Layer Transcoders (CLTs)—which learn a single, shared dictionary of features to approximate the input-to-output transformations performed by MLP layers across the entire model. In contrast, SFC draws its features from SAEs, trained separately for each layer and component (residual stream, MLP and Attention outputs). Delving into the technical comparison between CLTs and SAEs is beyond the scope of this section. Instead, we’ll focus on our framework with SAEs, how they are used to construct SFC circuits and what role the error nodes play in those circuits.
Sparse Feature Circuits: introduction and methodology
Feel free to skip this section if you're familiar with SFC methodology and jump directly to the next "Notes on the key metrics" section.
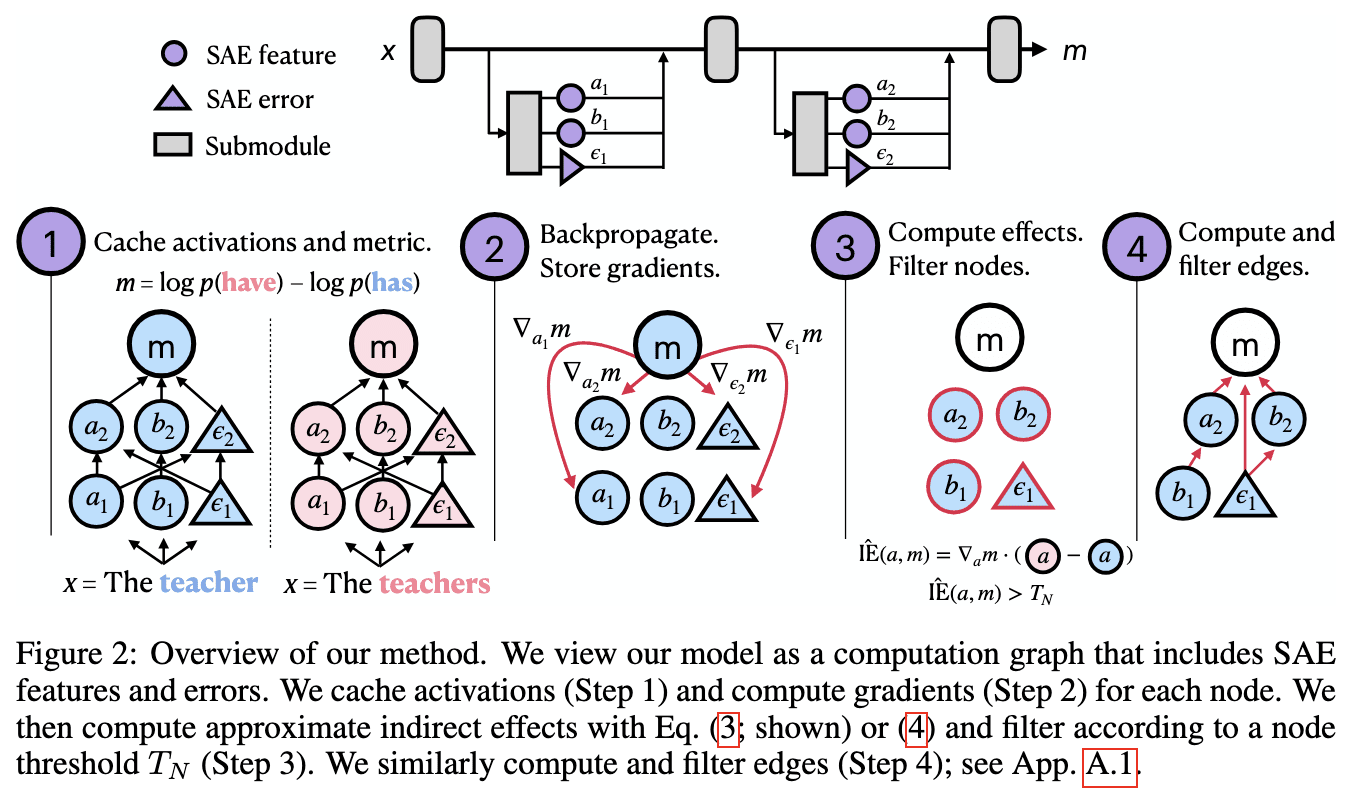
The key idea behind Sparse Feature Circuits method by Marks et al. (2025) is to automatically expand the model’s computational graphs into a sparse sum of SAE features activations (as in the above formula (1)). In this way, we move from the graph containing uninterpretable neurons to a graph which predominantly consists of (hopefully) interpretable SAE features and (hopefully) a small number of error nodes. We do this graph expansion for each major transformer submodule (resid_post, mlp_out, and attn_out activations, see here for a diagram if you’re unfamiliar with TransformerLens terminology) at each layer. This is visually demonstrated at the top of Figure 2 below, which we borrow from the original paper.
Then, having this expanded graph, we’re interested in how the model solves a particular task measured by some real-valued metric , i.e. which nodes are important (and how they connect) when the model solves the task. In the example of a subject-verb agreement task shown in the figure, the metric is the logit difference between the plural and singular versions of a verb.
To calculate the effect of each node on the metric , we run two counterfactual inputs through the model and collect their activation on each node: these are labelled as in the figure. To keep things named, we call the first counterfactual input as , and the second - . Then, we use the classical counter-factual notion of the node’s causal effect – Indirect Effect () (a.k.a. Activation patching effect):
That is, we patch the node’s activation from the “patched” input forward pass into the forward pass on the “clean” input. Then, we look at what effect it had on our metric: if the patching causes the model to switch its answer to the alternative “patched” answer, the term will be greater than ), making the IE score positive.
For example, suppose the value of node b2 is 1 when the (clean) input is “The teacher” and 2 when the (patched) input is “The teachers”. Our metric would be the logit difference between the “ have” and “ has” tokens (note that it should be negative for the clean input, and positive for the patched one). The effect of the b2 node in this computation graph is how much this metric increases when node b2’s value changes from 1 to 2 (i.e., from its “clean” to “patched” value).
Unfortunately, computing the IE score like that requires infeasible computational effort (we’ll need to rerun the model for every node patched), so in SFC we instead use two alternative gradient-based approximations[4] of this score. The first one is called Attribution Patching (AtP):
The second is a more expensive but more accurate approximation called Integrated Gradients (IG):
We invite the reader to check the original SFC paper for more details on why this is a reasonable thing to do, and also these excellent resources on attribution patching and activation patching.
Similarly, we use a gradient-based attribution to compute the edge weights to quantify how one node influences the other in the graph. The details are presented in A.1 appendix of the paper.
So, let's say we computed all the node AtP/IG scores and edge weights for a given task (averaged across the entire task-specific dataset) and its corresponding metric. That’s a lot of values! To be able to reasonably identify and visualize the resulting circuit, we’d like to focus on the most important nodes and their corresponding edges. We do this by applying a threshold-based filter to only keep the nodes that meaningfully shift our metric (i.e., have AtP/IG score above a certain threshold), and similarly filter for edges with weights above some threshold. The resulting set of nodes and edges after the filtering represents the final circuit.
- We generally refer to a node as “important” if it has a large enough AtP/IG score to pass this filtering.
- Similarly, we will compare different nodes “in importance” by comparing their AtP/IG scores.
But how do we learn anything useful from this circuit? The main step is to label the nodes using the usual methods for interpreting SAE latents (e.g., using human labellers or auto-interpretability to find patterns in tokens where features activate at). The result of this procedure hopefully produces a sketch of which variables (features) the model calculates in its forward pass, how they are computed from previous variables, and how they affect the final next token prediction for our task of interest.
Notes on the key metrics
The most important subsection from here is the "Faithfulness metric" subsection.
Attribution patching vs Integrated gradients
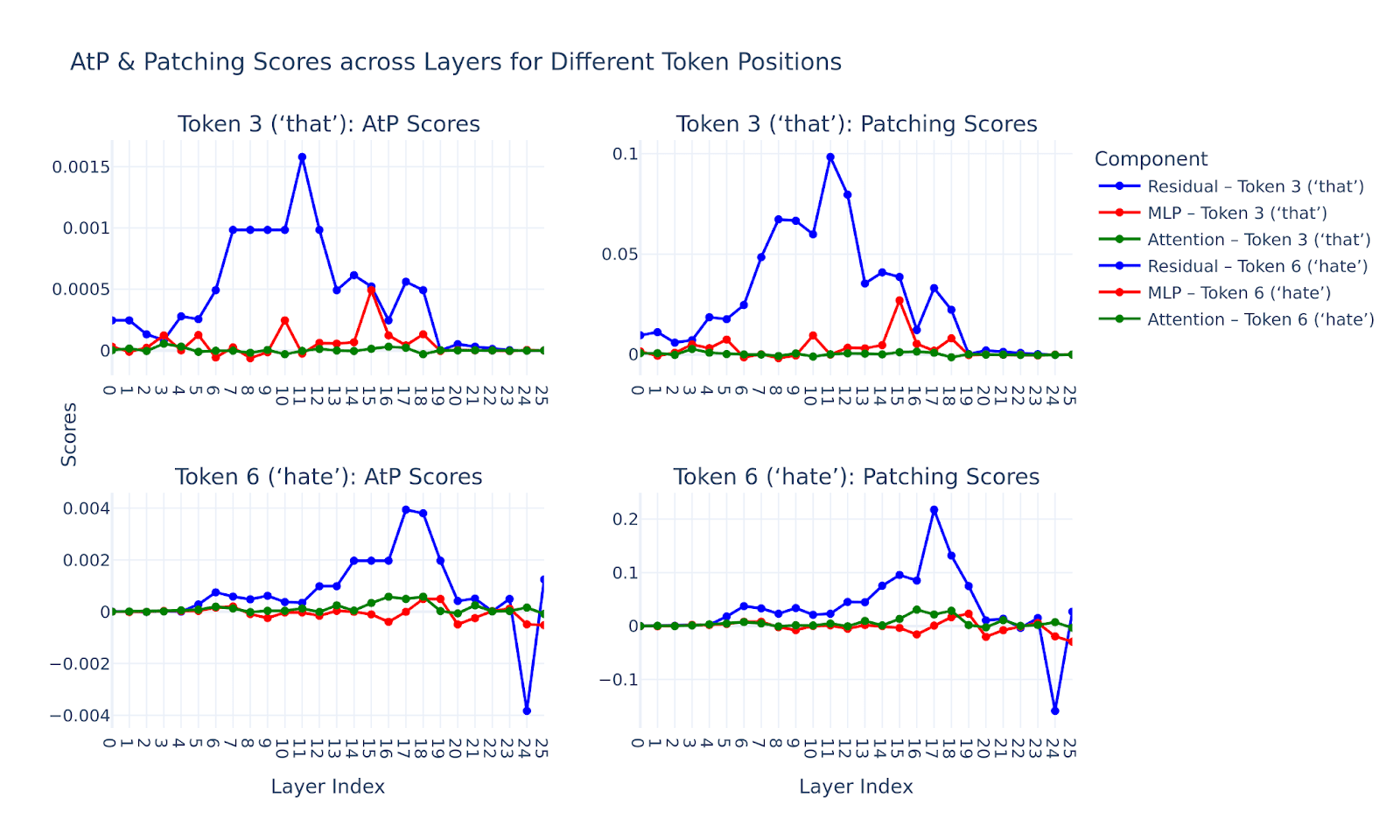
Both Attribution patching (AtP) and Integrated gradients (IG) metrics (or “scores”) are meant to be a cheap proxy for the “true” patching effect . As found by Marks et al. in the SFC paper (appendix H), both of them generally show high correlation with the patching effect, although IG takes a slight lead for early residual and MLP layers. Since the early layers don’t matter that much in our analysis (as the error nodes there have very weak AtP scores), we’ll rely on the AtP metric instead, given that it’s also much faster to compute.
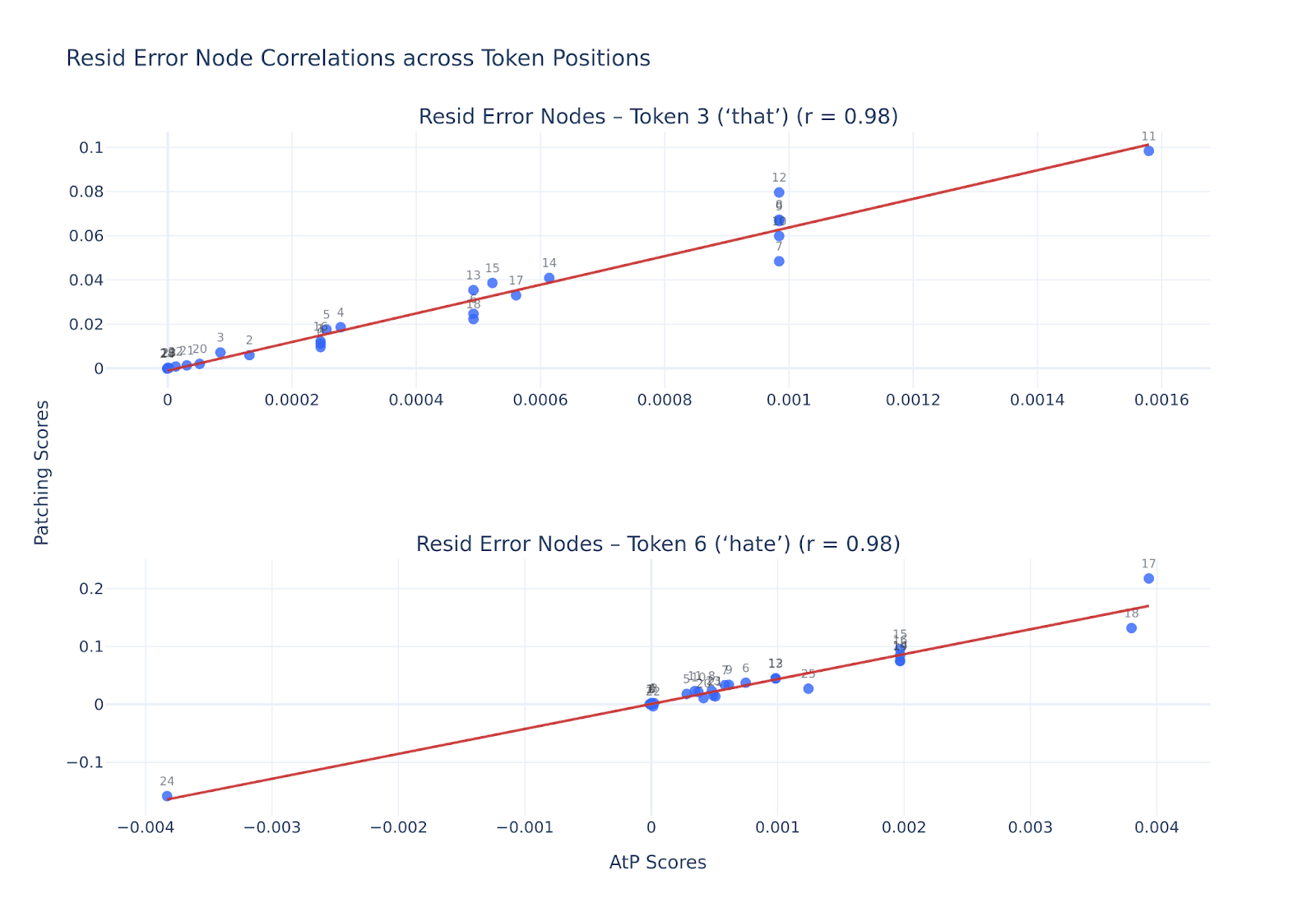
Another argument for our choice of AtP metric is that it’s almost perfectly correlated with the true patching effect of the residual error nodes, which are our key focus in this post. We demonstrate it on the example of Subject-Verb Agreement (SVA) across Relative Clause (SVA-RC) dataset from the SFC paper (we motivate our choice here in the “Subject-Verb Agreement case study” section), using Gemma-2 2B model with canonical Gemma-Scope SAEs. The general task presented by SVA-RC dataset is to predict the correct verb forms in the prompts like the one below:
“The girls that the assistants hate” go (example verb to predict)
We produce the figure below for our two key token positions, corresponding to “that” and “hate” words in the example above, where the most important error nodes are concentrated [5]
Each blue data point is the (AtP score, Patching effect score) of a single residual error node that comes from a specific layer (labelled above the points). The red line is the regression line, and the Pearson correlation coefficient is reported in the title.
So, if we accept the whole counterfactual theory of causality behind activation patching, our AtP scores meaningfully indicate the relative importance of the error nodes, as shown more clearly in the plot below.
Upon closer look there’s some small discrepancy between AtP and patching scores for residual nodes, visually because AtP scores seem to lose some detail producing flat ranges when the patching score varies; but overall the agreement is on the stronger side as indicated by the correlation coefficient above .
Faithfulness metric
The core question we haven’t touched on so far is “How can we be sure that our selected circuit faithfully corresponds to the ‘true circuit’ actually used by the model (i.e., that our circuit is faithful)?". This is where the faithfulness metric comes in. It assumes that a circuit is faithful if it alone achieves the same metric as the full model on our task of interest. “Alone” means that we compute faithfulness by ablating every node that is not part of the circuit, and compare the resulting performance (as reported by our metric value) with the performance of the full model. The ablation variant used is mean ablation – substituting the original nodes’ activations with their average activations across the entire dataset. This results in the formula below:
where
- – full model metric – is the metric value that the original model achieves for a given prompt
- – circuit metric – is the metric value when everything outside circuit C (a collection of selected SAE nodes and error nodes) is mean-ablated
- – empty circuit metric – is the metric value when every node is mean-ablated
The intuition behind this formula is that it captures the proportion of the model’s performance our circuit explains, relative to mean ablating the full model ("which represents the “prior” performance of the model when it is given information about the task, but not about specific inputs" as explained in the paper). So, when the circuit performance equals to the performance of the full model: ; and when the circuit performance is as bad as in the empty circuit case: .
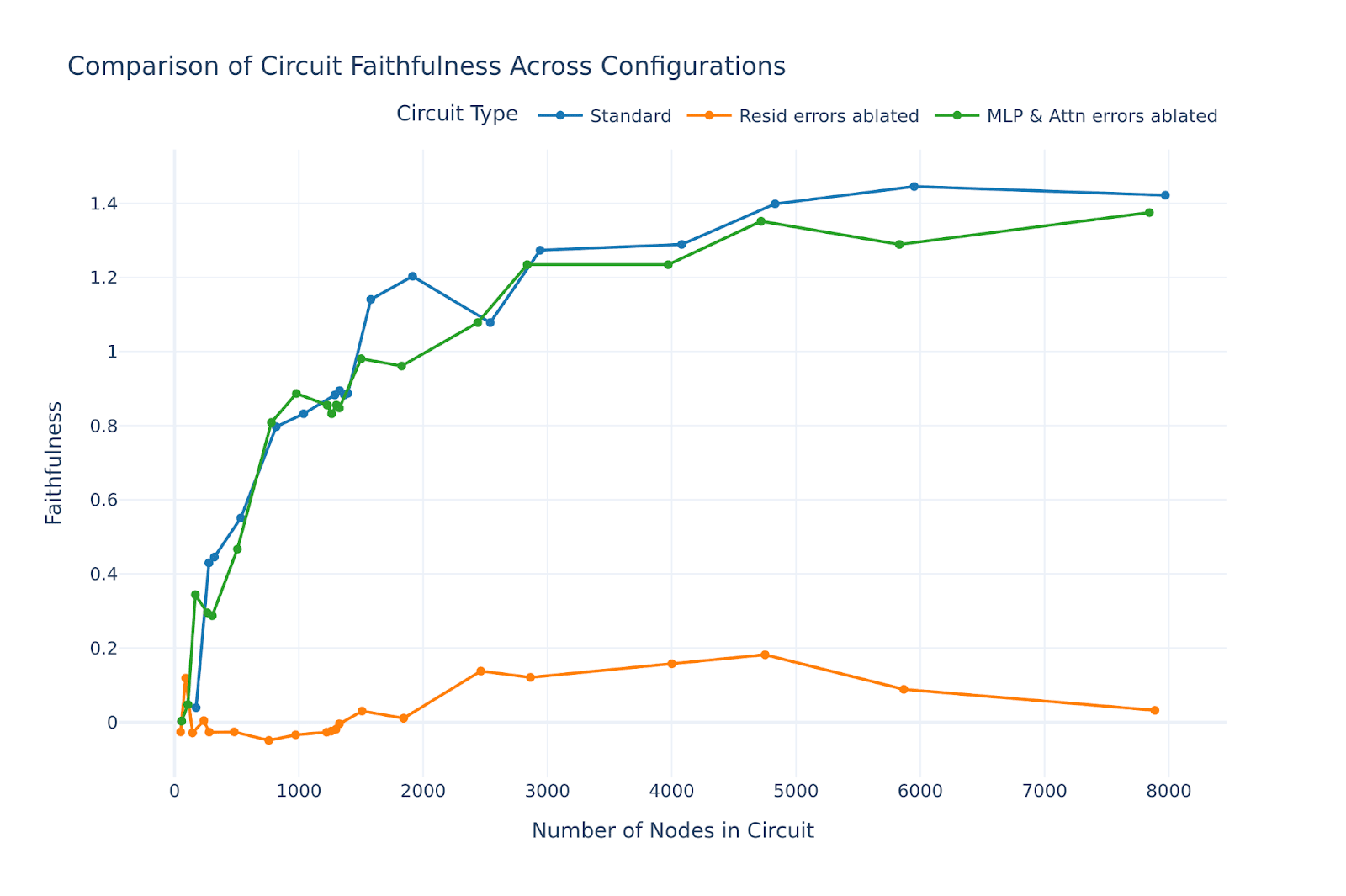
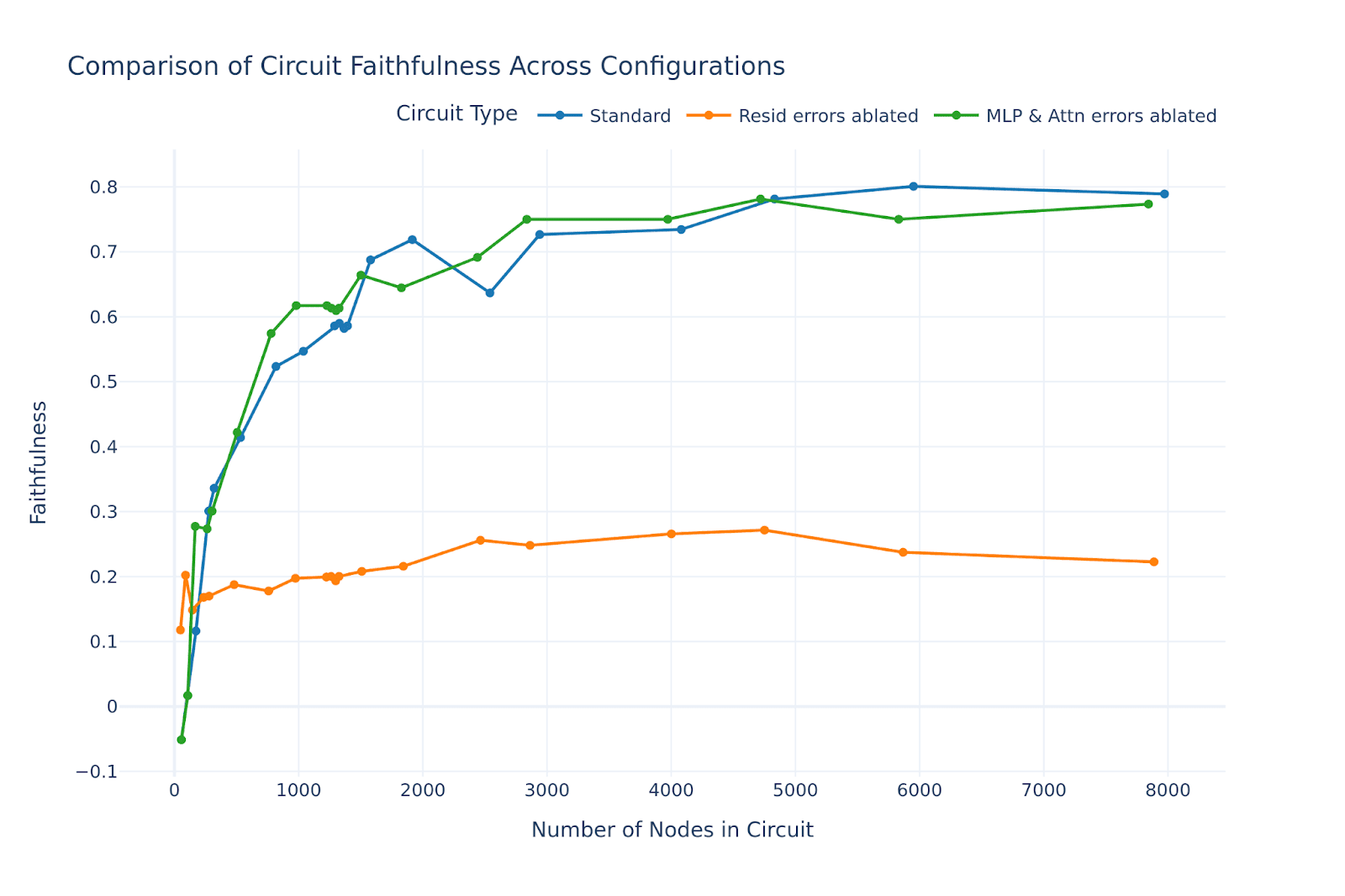
We began with reproducing the SFC paper results related to circuit evaluation using this faithfulness metric, and for the SVA-RC task we obtained the following figure showing how faithfulness changes with different circuit sizes, which is a replication of Figure 3 in the original paper.
Here we swept through a number of thresholds, and evaluated every circuit corresponding to each threshold (i.e. circuit nodes were selected based on that threshold). We also performed two other variants of this evaluation: when MLP & Attention error nodes are ablated (green line), and when residual error nodes are ablated (orange line). Consistently with Marks et al., the figure reveals that ablating residual error nodes is much more destructive to the model than ablating MLP & Attention error nodes. This is why we focused on the residual error nodes only in this post.
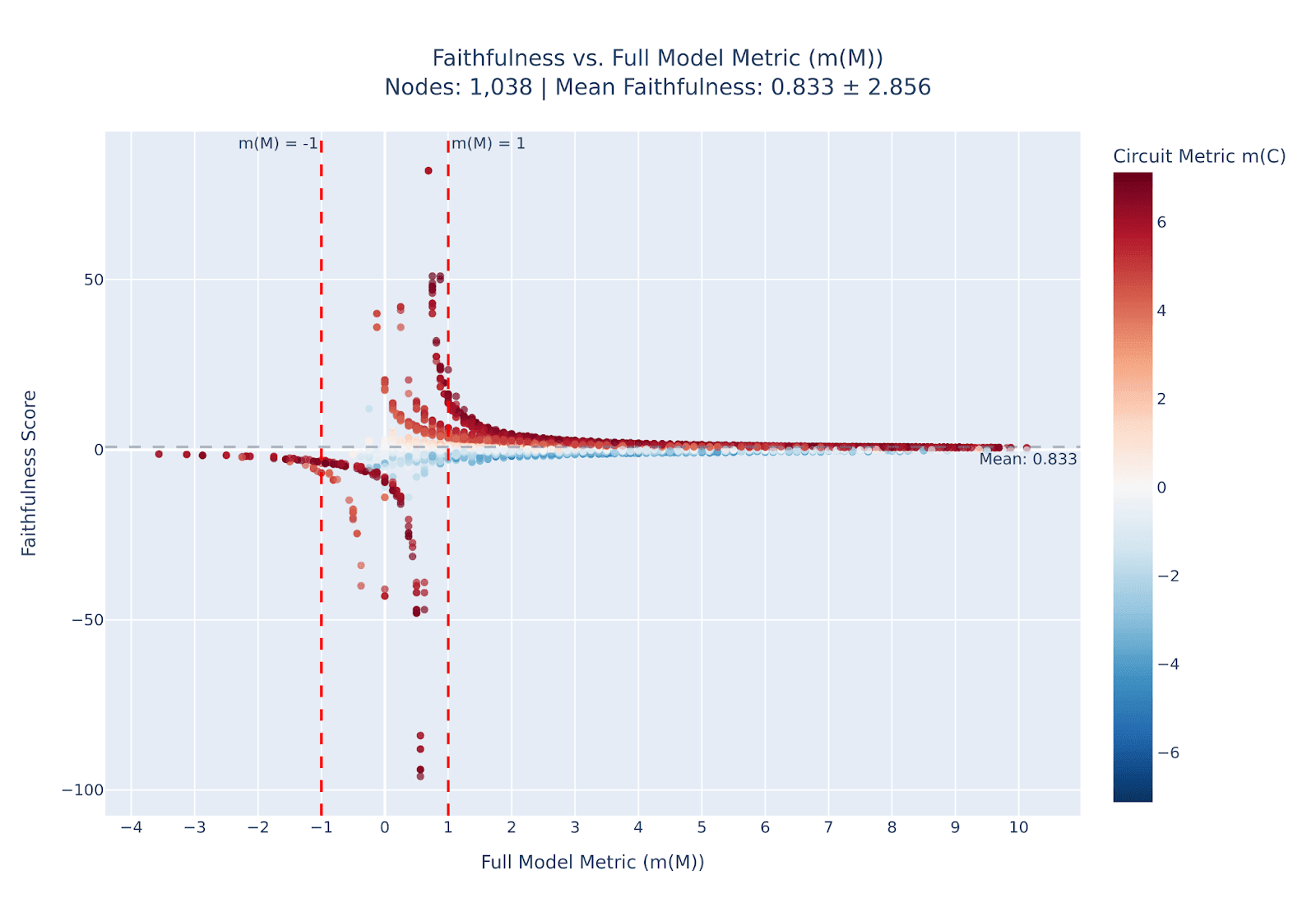
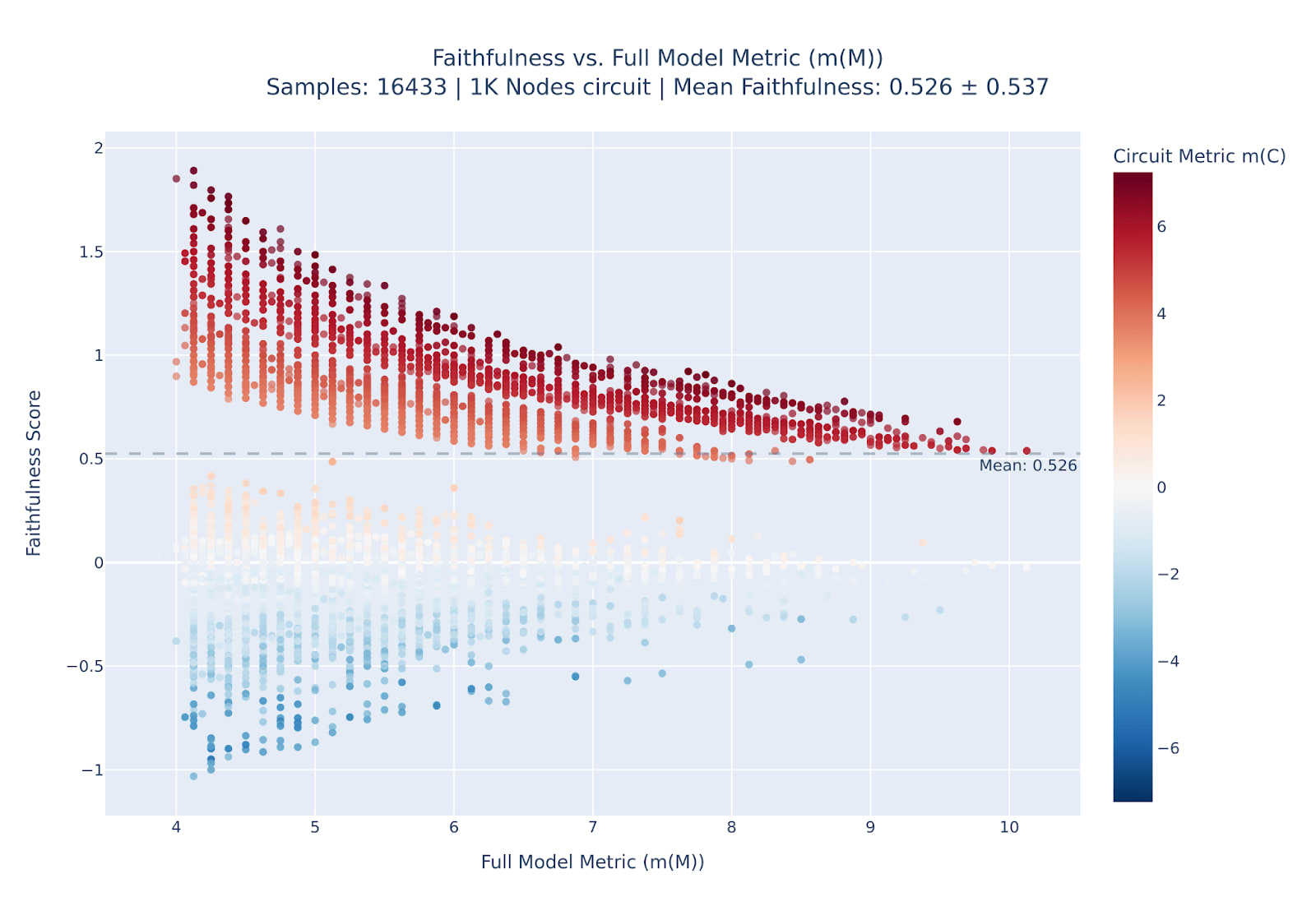
What the figure doesn’t reveal is how much the faithfulness score varies across different prompts: the value we plotted here is the mean faithfulness averaged across all the prompts ("faithfulness" and "mean faithfulness" are generally used interchangably). And this is quite important to know, because the mean value can be heavily influenced by outliers. To explore this, we created a scatter plot of individual faithfulness scores against the full model metric , with each point colored by the corresponding circuit metric —where, for all metrics, higher values indicate greater model confidence in the correct verb completion (answer) over the incorrect one. In the title we report the size of the example circuit we selected for this plot, and what the resulting mean and standard deviation of the faithfulness scores are.
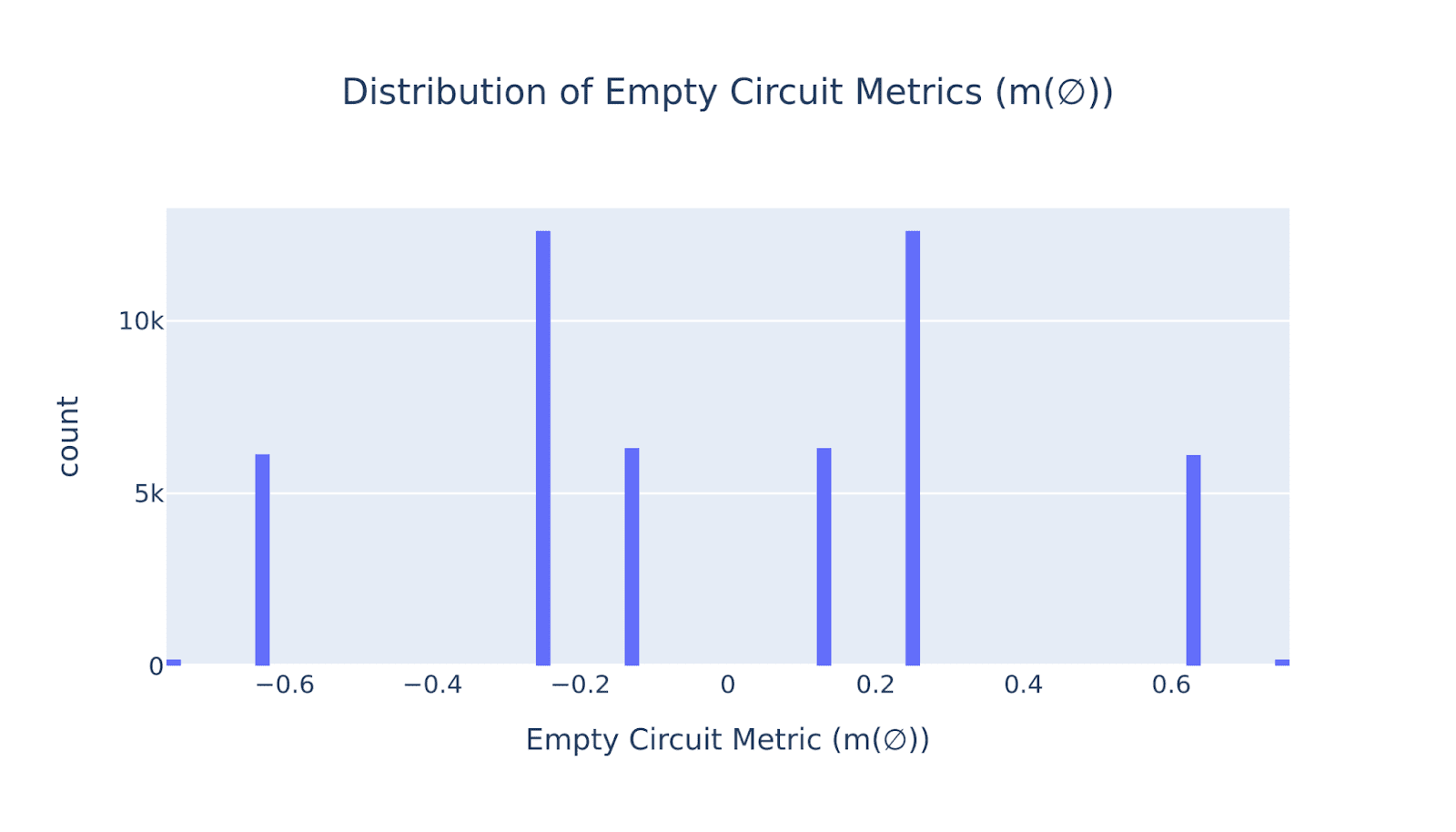
We can now see that there are plenty of bad outliers way outside the “normal” faithfulness range! The way we plotted this also reveals the culprit: as indicated by our red vertical lines, most outliers lie within the region when the model is not confident in the correct answer itself, having the value between -1 and 1. In that case, the denominator in the faithfulness formula (5) is much more likely to explode, since the empty circuit metric also lies between -1 and 1 as we show in its histogram below.
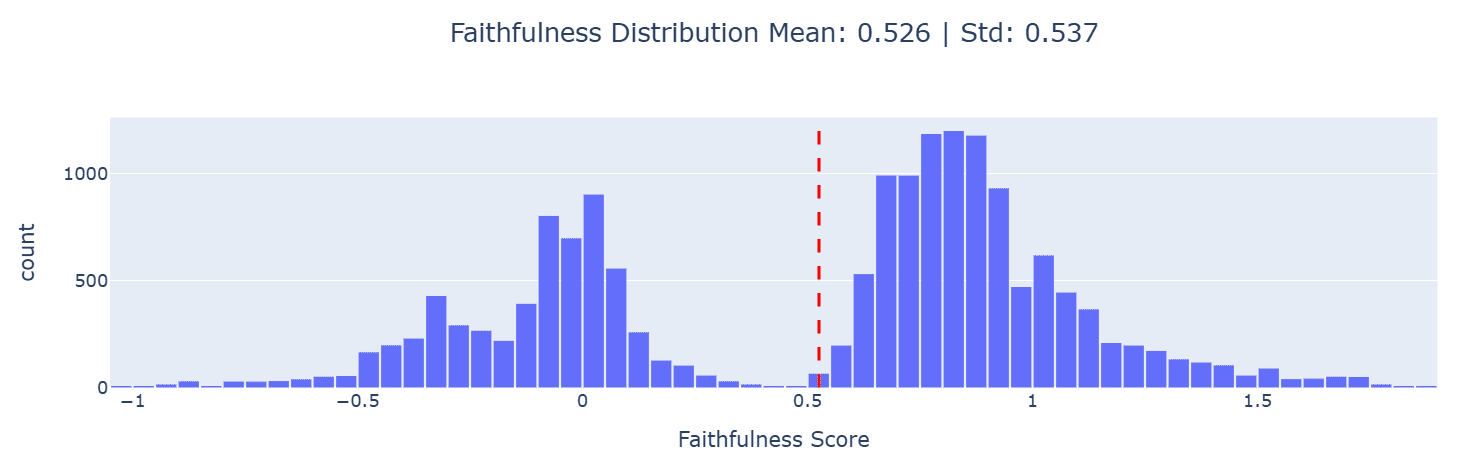
A natural way to filter those outliers is to focus on the right-hand side of our outliers plot, i.e. keep only those samples where the model is confident in the correct answer, having with some threshold . We perform this filtering using a value , which kept 16433 out of our original 50,538 samples. This resulted in a much better distribution of faithfulness scores as one can see below.
Interestingly, the new distribution shows a clear bimodal pattern, suggesting that our example 1K-sized circuit “works well” about half the time, while failing almost completely the other half. Also note how the faithfulness score dropped: from 0.833 value for the selected threshold down to 0.526. This suggests that our original faithfulness evaluation was heavily influenced by outliers, so we repeated it on this filtered dataset, resulting in the below figure.
The figure suggests that faithfulness dropped by around 0.3 compared to the original dataset.
Now, we don’t make any claims about the original SFC version of this experiment, not least because we used a different metric for selecting circuit nodes—AtP instead of IG. (We only briefly checked that the features we identified and their relative scores were broadly consistent with those in the original SFC circuit, but this wasn’t a robust verification). The takeaway that’s important to us is that if we want to use the faithfulness metric in our setting, we’d better make sure to filter those outliers, so we do as already mentioned: only keep the scores that satisfy .
We visualize the resulting dataset below using the previous faithfulness scatter plot technique, using the sample circuit with ~1K nodes to compute the faithfulness scores.
This dataset was used for all our further experiments in this post.
Subject-verb agreement case study
Our investigation of the error nodes began with posing a simple question: “Okay, the paper presents a bunch of nice-looking circuit visualizations. Did anyone stare enough at those circuits to figure out what the error nodes might be doing?”. After all, even if the node is uninterpretable using traditional techniques, the circuit contextualizes the nodes: we can see what nodes they are “computed from” and what further nodes they influence the most. Of course there are important assumptions [6] needed for this to yield anything useful, but we thought it’s worth trying anyway!
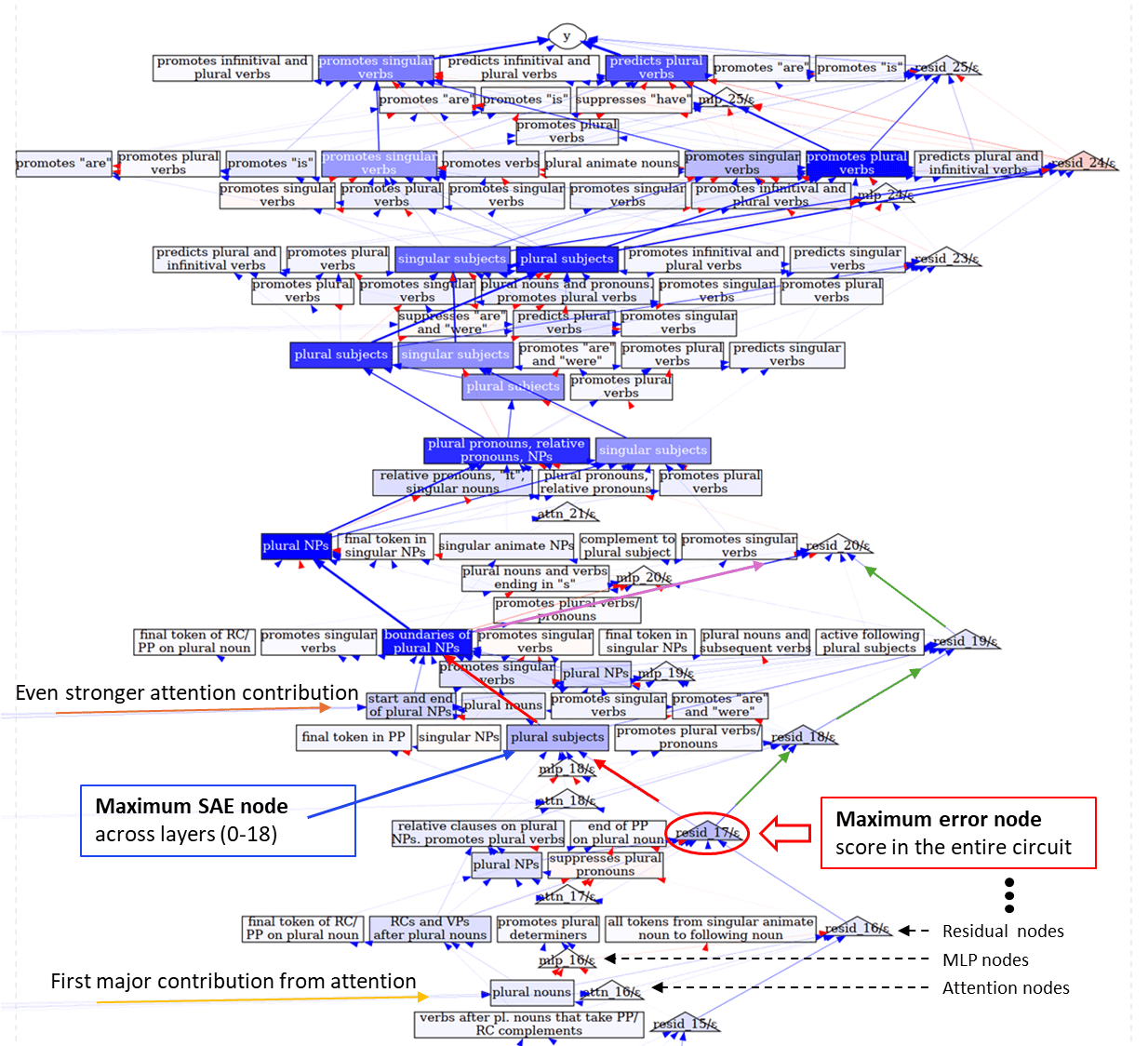
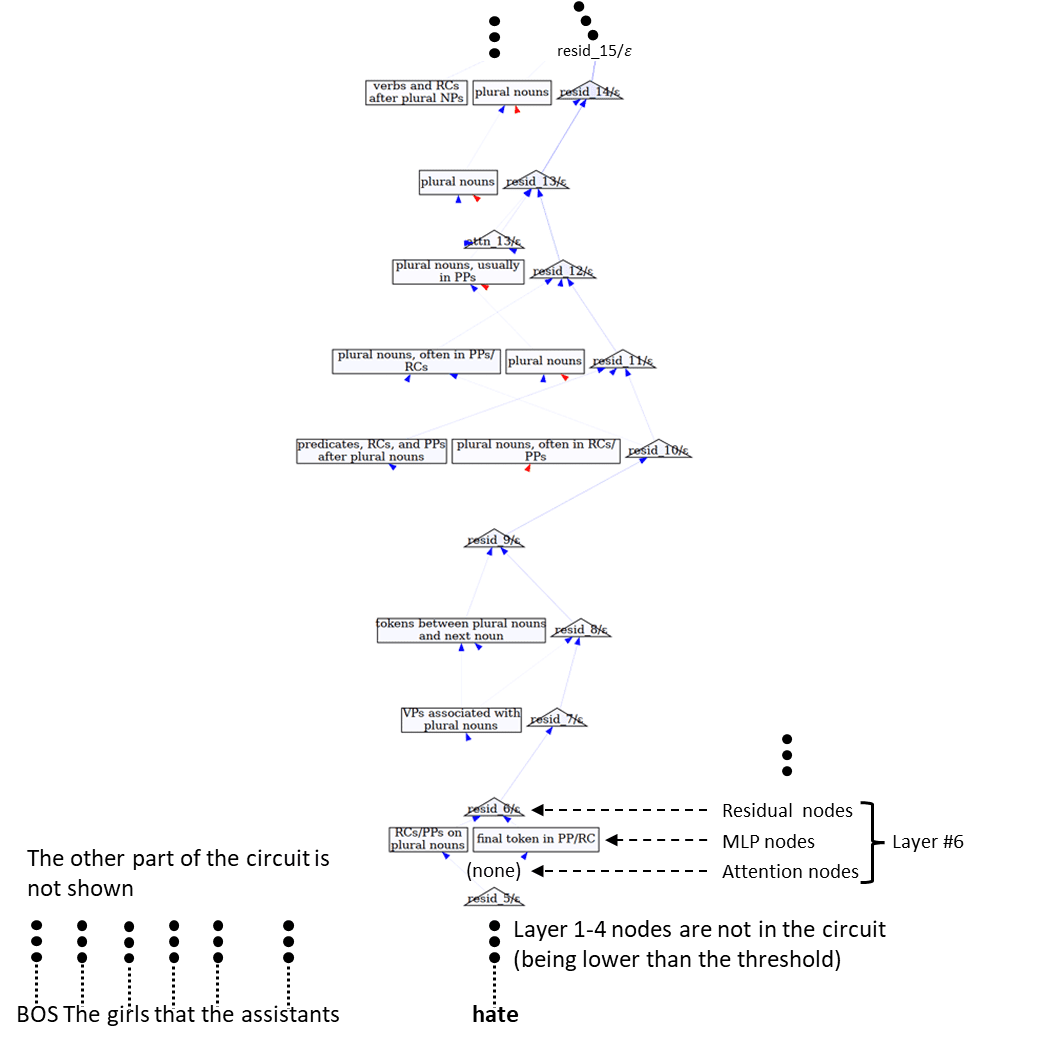
So we went through each circuit from the SFC paper’s Appendix, and the most general pattern regarding error nodes we found is what we are going to describe below. We introduce it using the example of the Subject-Verb Agreement (SVA) circuit across Relative Clause (SVA-RC) for Gemma-2 2B – the one where the model needs to predict a correct verb form in sentences like “The girl that the assistants hate…” (where the continuation is e.g. “goes”). The first part of the circuit is visualized in the figure below, borrowing it from Marks et al. – Figure 8 of the original paper [7]. We focus specifically at the nodes active at the last token (“hate”), because the most “weighty” error nodes (with the highest AtP scores) are active specifically at that token.
The other part of the legend (besides the part shown in the figure) is that SAE feature nodes are shown in rectangles, error nodes – in triangles, the color intensity indicates the magnitude of the AtP score (e.g., more blue = more important), and the color itself indicates the sign of the score. Blue nodes are those which have positive effect (patching them = good for predicting the correct form), while the red ones have the opposite effect (nodes of this type are not shown above, but will be shown in the upper part of the circuit).
The first part of the circuit is not particularly interesting, and this is consistent with the explanation given in the paper (bolding is our own):
First, we present agreement across a relative clause. Pythia (Figure 7) and Gemma (Figure 8) both appear to detect the subject’s grammatical number at the subject position. One position later, features detect the presence of relative pronouns (the start of the distractor clause). Finally, at the last token of the relative clause, the attention moves the subject information to the last position, where it assists in predicting the correct verb inflection. Gemma-2 additionally leverages noun phrase (NP) number tracking features, which are active at all positions for NPs of a given number (except on distractor phrases of opposite number).
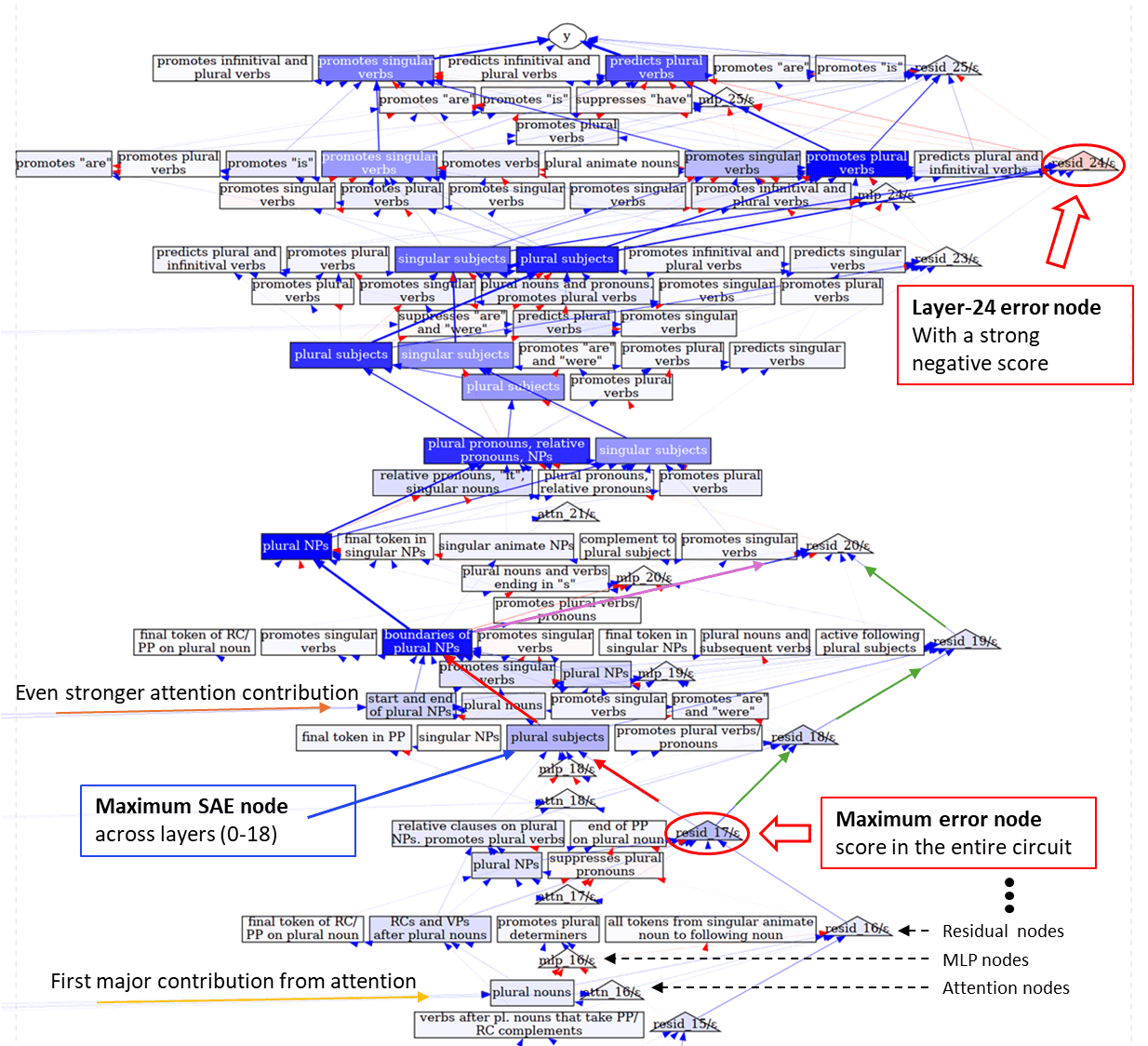
And according to the circuit, the attention hasn’t yet moved the key subject information in the first part of the circuit shown above (which happens only at layer #16), so it’s no surprise that there’s not much computation the model can do at the last token before this happens. The more interesting part of the circuit is the second part, which we present below (once again, borrowed from Figure 8 of the paper with custom annotation) along with our observations about it.
Key observations about the SVA circuit
Focusing on our custom annotation above (colorful arrows and text labels), we introduce the following observations:
- Peak error node at layer-17 (circled in red) directly influences the most important (by AtP score) SAE feature – “Plural subject” feature at layer-18 – encountered in the circuit so far (before layer 19) - red line
- This is the first time in the circuit when the error node influences a downstream SAE node with such attribution weight – before that the error nodes were mostly influencing other error nodes (downstream neighbours).
- The error nodes experience a sharp decrease in AtP score exactly after layer 18, when they stop influencing any of SAE features - green line. That is, starting from layer 18 this error node branch no longer has any effect on other SAE nodes.
- There’s also a weird strong connection between the most important feature at layer 19 and the resid_20 error node - purple line. It’s weird because unlike most of the “strongest connections” resid_20 error (endpoint of the edge) has a very low AtP score and doesn’t influence any of downstream nodes. [8]
Motivated by these observations, we went on to investigate the following hypothesis. Note that the formulation below is deliberately quite naive/narrow and most definitely isn’t the only explanation of these observations (we discuss other alternatives later in the post). It served only to guide our further experiments in an effort to refine it:
- Error nodes (*up to layer 23) are important only because they are intermediate steps in computation of the most important SAE features that start to kick in at layer #18
- Once the most important SAE features are computed, they “take the floor” from the error nodes, so the latter are no longer important.
- Starting from layer 18, error nodes and SAE features “swap their roles”: important SAE features strongly influence low-scoring error nodes (purple line, but also in the next layers), as if these error nodes were kind of a “leftover” from these important SAE features.
But what does it even mean to be “intermediate steps in computation?” of SAE features? Why are these steps not captured by other SAEs in earlier layers? Well, what makes this hypothesis meaningful and even plausible is the Anthropic’s theoretical result on cross-layer superposition, which we are going to detail in the next section.
Error nodes as a result of cross-layer superposition
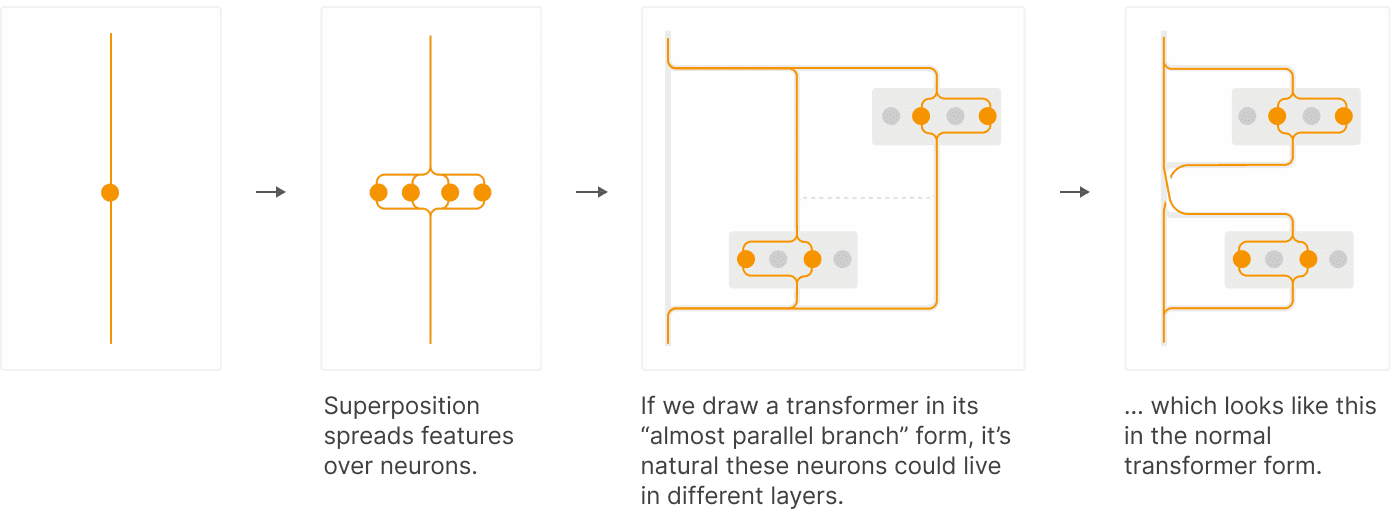
We recommend checking the original Anthropic’s introduction to the concept of cross-layer superposition, presenting here only a brief summary. In short, it extends the idea of the original superposition hypothesis to multiple layers, suggesting that features can be represented in superposition not only within the single activation space (layer), but also scattered across multiple layers. Here’s how Anthropic describe it:
If we consider a one-step circuit computing a feature, we can imagine implementations where the circuit is split across two layers, but functionally is in parallel. This might actually be quite natural if the model has more layers than the length of the circuit it is trying to compute!
(the figure is borrowed from the same Anthropic’s post)
So, tying it back to our terms, we refer to the combinations of neural activations that represent the feature in different layers as different computational steps of that feature, which are depicted as orange circles on the right of the above figure. We hypothesize that the final feature representation is formed when all of its computational steps have been added to the residual stream (top-right of the above figure), and that’s when residual SAEs should be able to capture it. Intermediate steps (bottom-right of the above figure) are probably not real features as in the “properties of the input” sense and hence are not captured by an SAE, serving more as internal variables (“computation trackers”, “useful cache” etc.). But keep in mind that all this is fairly speculative and we don’t even agree on it completely as co-authors.
Building on this framework, Anthropic go on to introduce their new dictionary learning model at that time:
If features are jointly represented by multiple layers, where some of their activity can be understood as being in parallel, it's natural to apply dictionary learning to them jointly. We call this setup a crosscoder …
For unfamiliar readers we introduce crosscoders from scratch later in the post (Acausal crosscoder analysis section), and also invite you to check the original Anthropic’s introduction. For the rest of this section, we’ll assume the basic familiarity with crosscoders.
So, what (if any) evidence do we have behind cross-layer superposition? Later in the post, Anthropic present the following experiment
- train an acausal variant of the crosscoder
- sample a random selection of features (each feature = a separate line on the plot below)
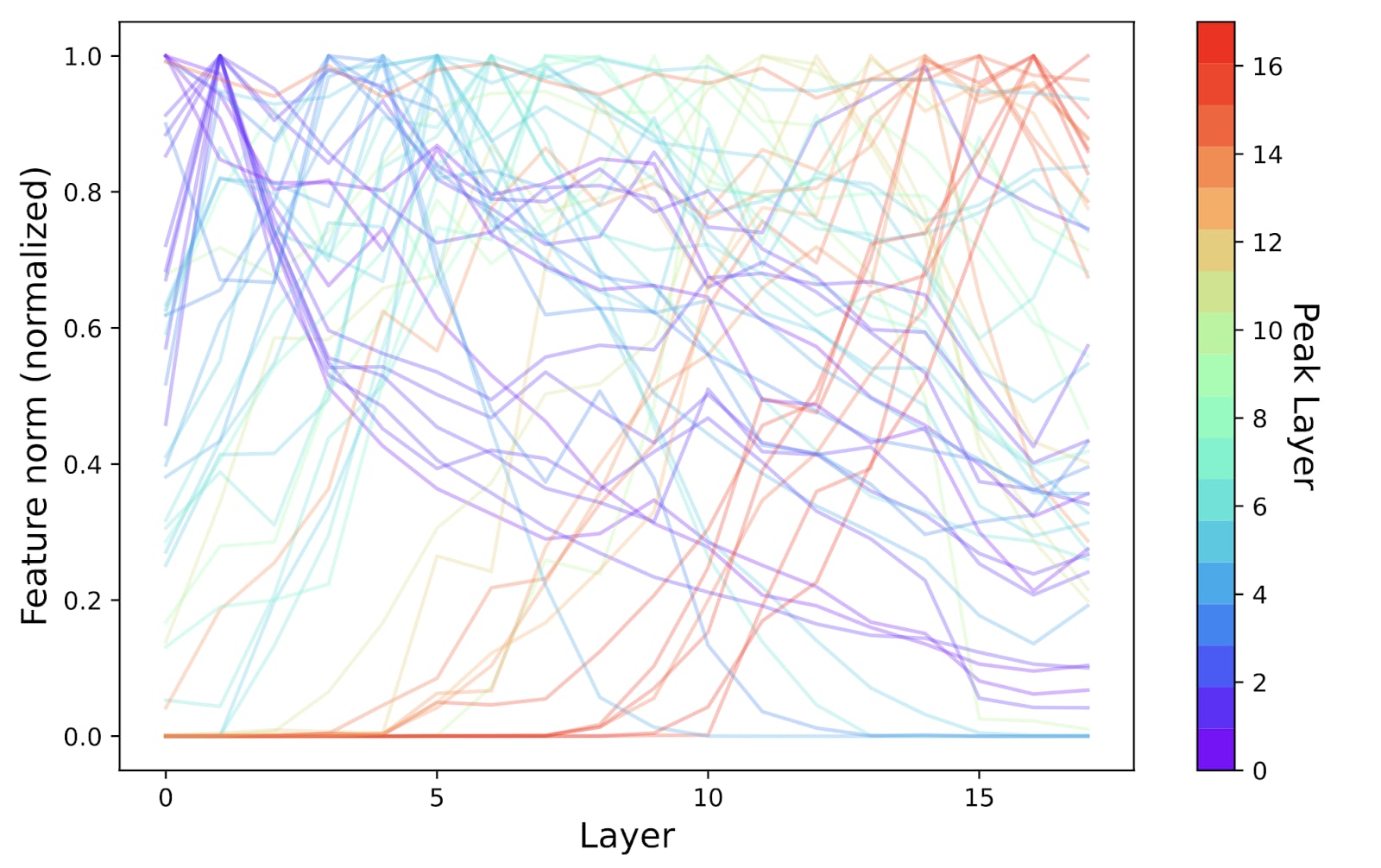
- plot the norms of the decoder directions for the sampled features across the layers of the model. The idea is that we can treat the decoder direction norms as a proxy of “how active” the feature is at the layer, and since we have one decoder per layer, it allows us to inspect the “feature activity” in the entire model.
And here is Anthropic’s interpretation of this plot.
We see that most features tend to peak in strength in a particular layer, and decay in earlier and later layers. Sometimes the decay is sudden, indicating a localized feature, but often it is more gradual, with many features having substantial norm across most or even all layers.
…Is the existence of gradual formation of features distributed across layers evidence for cross-layer superposition? While it's definitely consistent with the hypothesis, it could also have other explanations. For example, a feature could be unambiguously produced at one layer and then amplified at the next layer. More research – ideally circuit analysis – would be needed to confidently interpret the meaning of gradual feature formation.
Well, the last part is what we aim to do in this post! Reformulating our initial narrow hypothesis in terms of cross-layer superposition, we speculate that our “Plural subject” feature at layer-18 is computed under cross-layer superposition, and the long “tail” of the error nodes in the previous layers are its intermediate representations/computational steps.
Ablation and restoration experiments
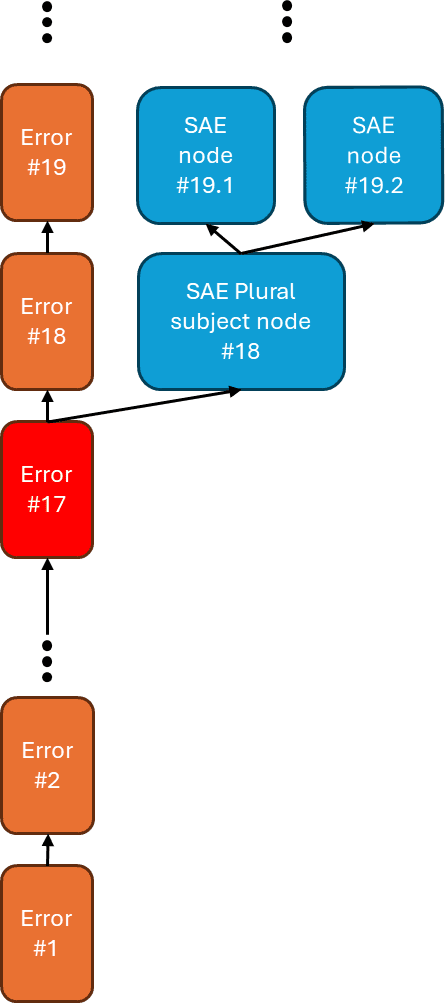
The idea behind our first experiments which we named as Ablation & Restoration is as follows.
If our cross-layer hypothesis for the residual error nodes in the SVA-RC circuit is true, then we should be able to restore the model’s performance when all residual error nodes are ablated just by restoring the value of the “plural subject” feature at layer 18. After all, if the model just uses the error nodes to represent that feature, the ablation effect (faithfulness dropping down to zero) should be completely mitigated if we restore that feature’s value (faithfulness returns up to 1) [9]. This is schematically shown in the diagram below
This means that if we restore the feature’s value and nothing happens, the hypothesis is false in its current form. However, if we restore the feature’s value and we see a significant increase in faithfulness, it won’t imply that the hypothesis is true. Indeed, there could be another computational path that goes through the error nodes only, and we’re just restoring one branch of it as shown below.
So, even though the outcome of this experiment is either “the hypothesis is false” or “the hypothesis may be true, but we don’t know all the computational paths”, we thought this is a useful information gain. To gain even more information, we also
- Restored features from different layer ranges, i.e. not just from the layer 18 but also in layers 18-19, 18-20 and so on
- Restored a different number of features, i.e. not just top-1 plural subject feature, but generally all the features with top-K AtP score from a given layer range (and varying K). For the first experiment, we restored only the features of the residual SAEs.
- We ablate error nodes and restore features only at a single last token, which corresponds to the circuit part we showed in the circuit diagram above.
One note before showing the resulting plot is that we mean-ablated all error nodes except at the last two layers (24 and 25). This is because our hypothesis is only meant to explain the main bulk of the error nodes, and it doesn’t really apply when all features should already be fully represented in the residual stream (as in the ’resid_post_25’ case, right before the unembed matrix). We also ablate the intermediate late nodes between layers 18 and 24 because they have a fairly low AtP score (even though our hypothesis doesn’t directly apply for them), but later we’ll show a version of this experiment when we don’t do that and only ablate nodes up to layer 18.
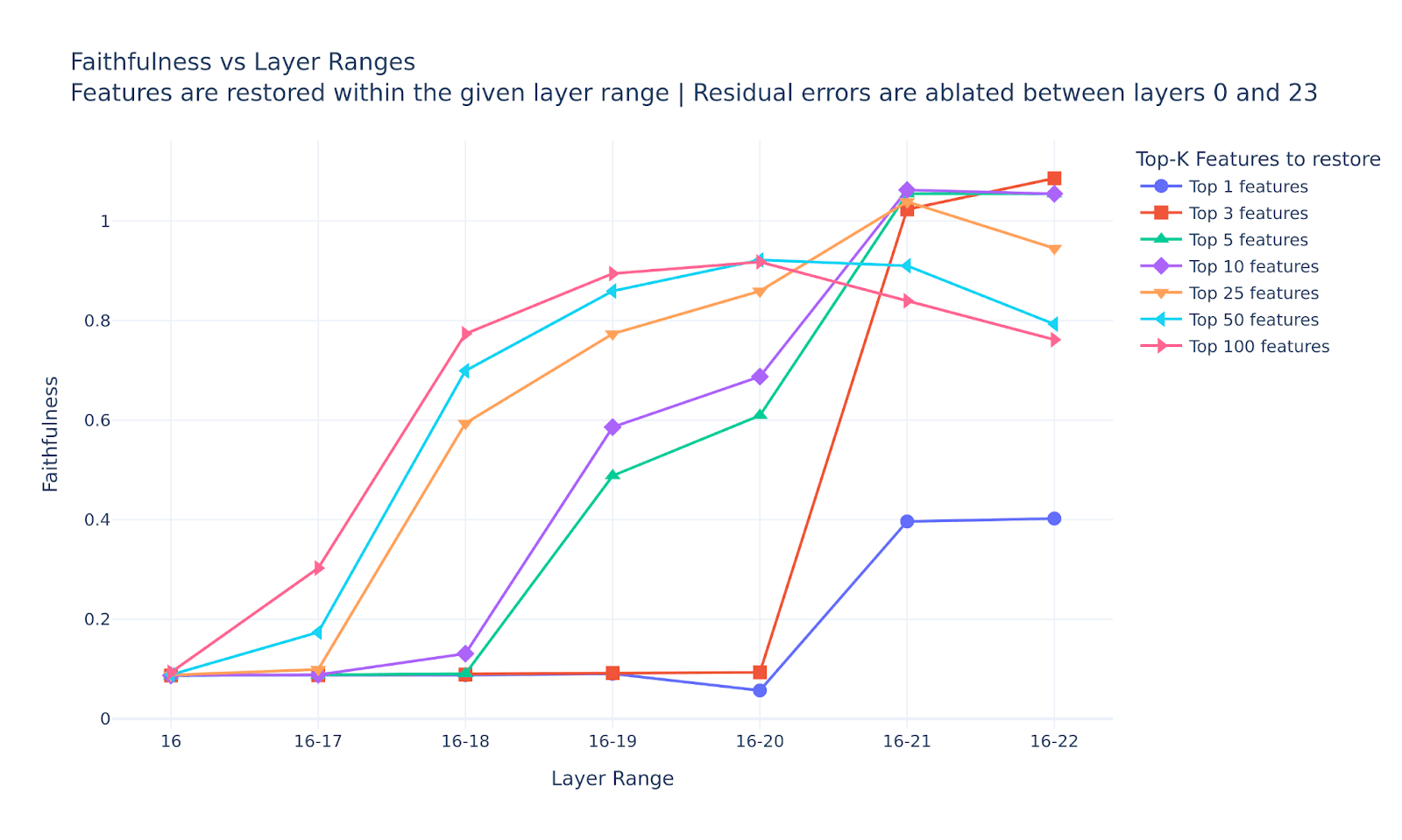
As mentioned above, we measure the outcome of our single ablation & restoration trial with “how much our model’s performance is restored when we ablate all residual last-token error nodes up to second-to-last layer”, operationalized in terms of the faithfulness metric (which is 0.13 if we don’t restore any features). So, plotting the faithfulness metric for each trial results in the figure below:
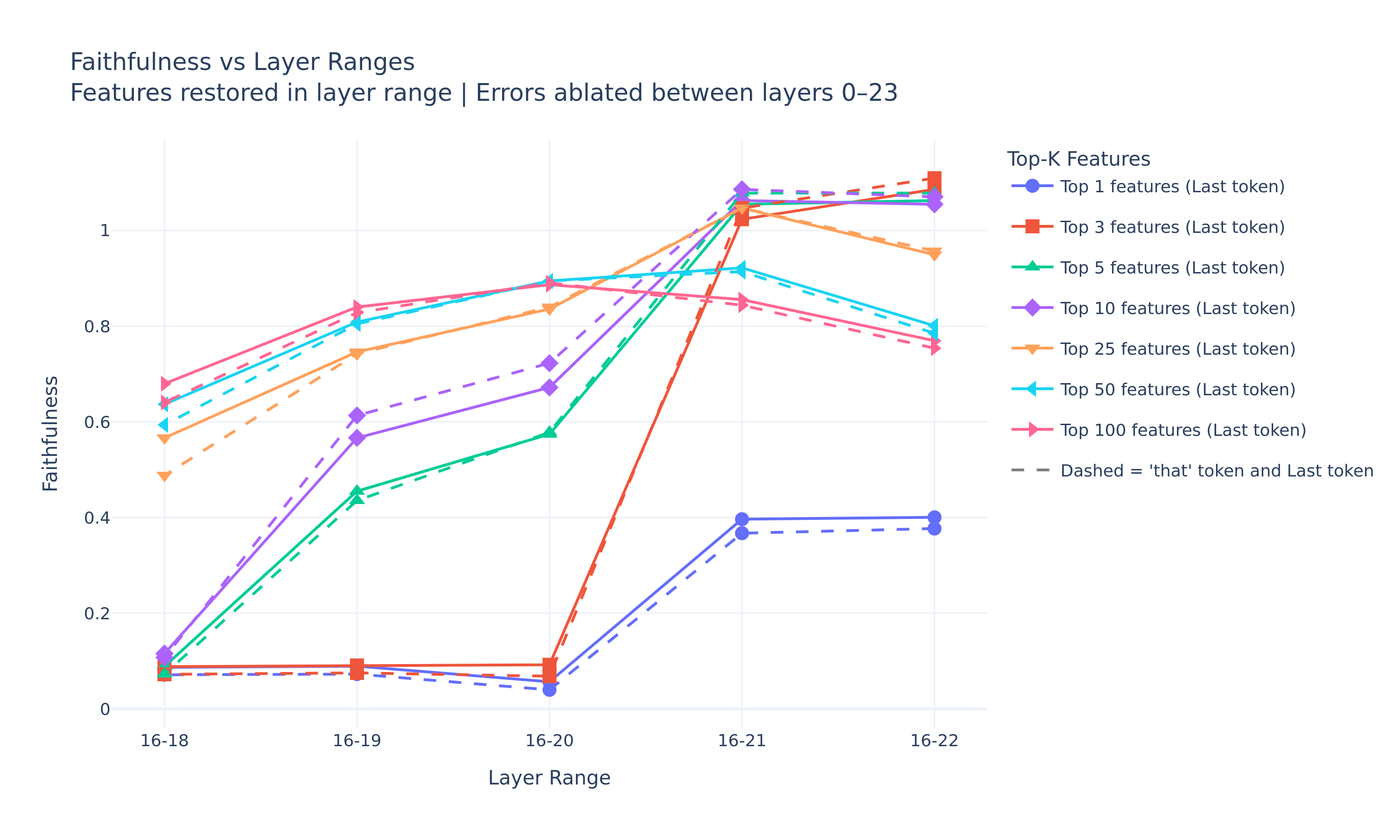
This surely seems like a useful update to us:
- The naive version of our hypothesis was false - restoring only top-1 feature (plural subject feature) from layer 18 does nothing.
- However, if we increase the number of features to restore up to 25, we see that restoring features from layer 18 is actually quite impactful compared to the earlier layers, boosting up faithfulness up to 0.6. The results seem much better when we also restore the features from layer 19, which shows a significant boost already for 10 features.
- The ablation effect is completely mitigated when we restore as little as 3 features from layers 16 up to 21.
Okay, so of course it’s a lot messier than our naive hypothesis suggested—but something interesting does seem to be happening in layers 18–19, since we can restore faithfulness to 0.8-0.9 by intervening on just those features. This suggests that, even if we’re not capturing all the computational paths influenced by the error nodes, one of the key paths does go through those features—just not through a single one, but rather a subset of about 25.
Additionally we performed several variations of this experiment:
- Initially, we included the 16–17 layer range in our feature restoration experiments to show that these layers are not nearly as impactful as restoring features from later layers—consistent with our hypothesis. However, it’s unclear how much this early range contributes to the overall effect when combined with downstream restoration, so we also created a version of the plot excluding the 16–17 range.
- Furthermore, to test a stronger version of the hypothesis, we also ablated the error nodes from the earlier “that” token in the prompt, where nearly all the other high-scoring error nodes reside. Here, one can check the same Figure 8 of the SFC paper and notice that unlike last-token error nodes, “that” token error nodes fade off after strongly influencing attention SAE nodes at the last-token position; so, in this version of the experiment, we also restored attention & MLP nodes on top of residual ones.
The results of both of these modified experiments are given in the plot below. Solid line corresponds to the 1st experiment, dashed line – to the 2nd.
As we can see, the outcome is very similar to the original version here for both experiments, indicating that a) restoring 16-17 layer nodes doesn’t have a major effect by itself; b) the restoration procedure is effective not only at the last token (if MLP & Attention nodes are included).
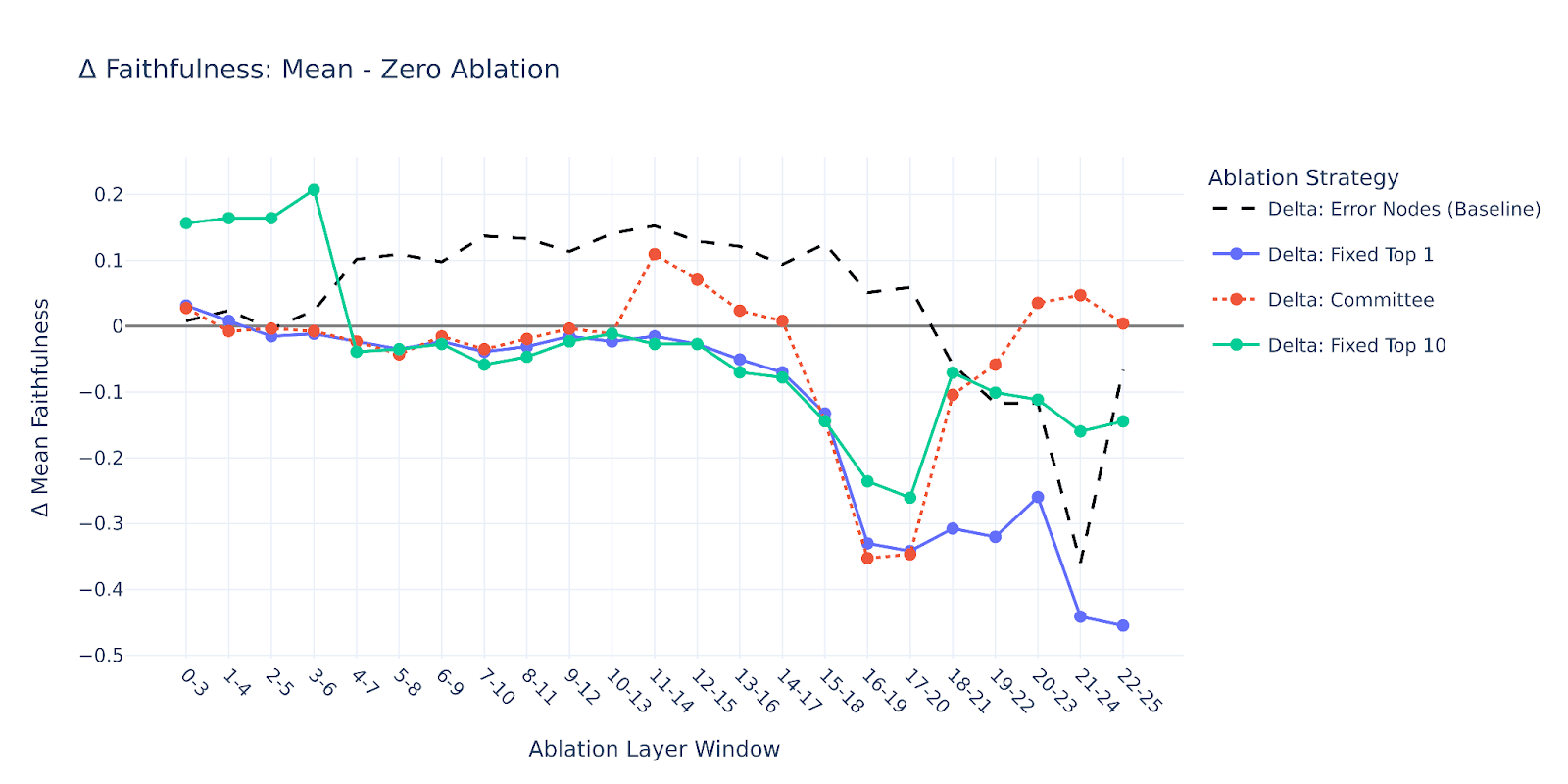
Lastly, we were quite curious what would happen if we zero-ablated the error nodes instead of mean-ablating them. It turns out that in this scenario, the faithfulness is boosted all across the board for our principal layer ranges (18+), as shown below (solid line = original experiment; dashed line = new zero ablation variant).
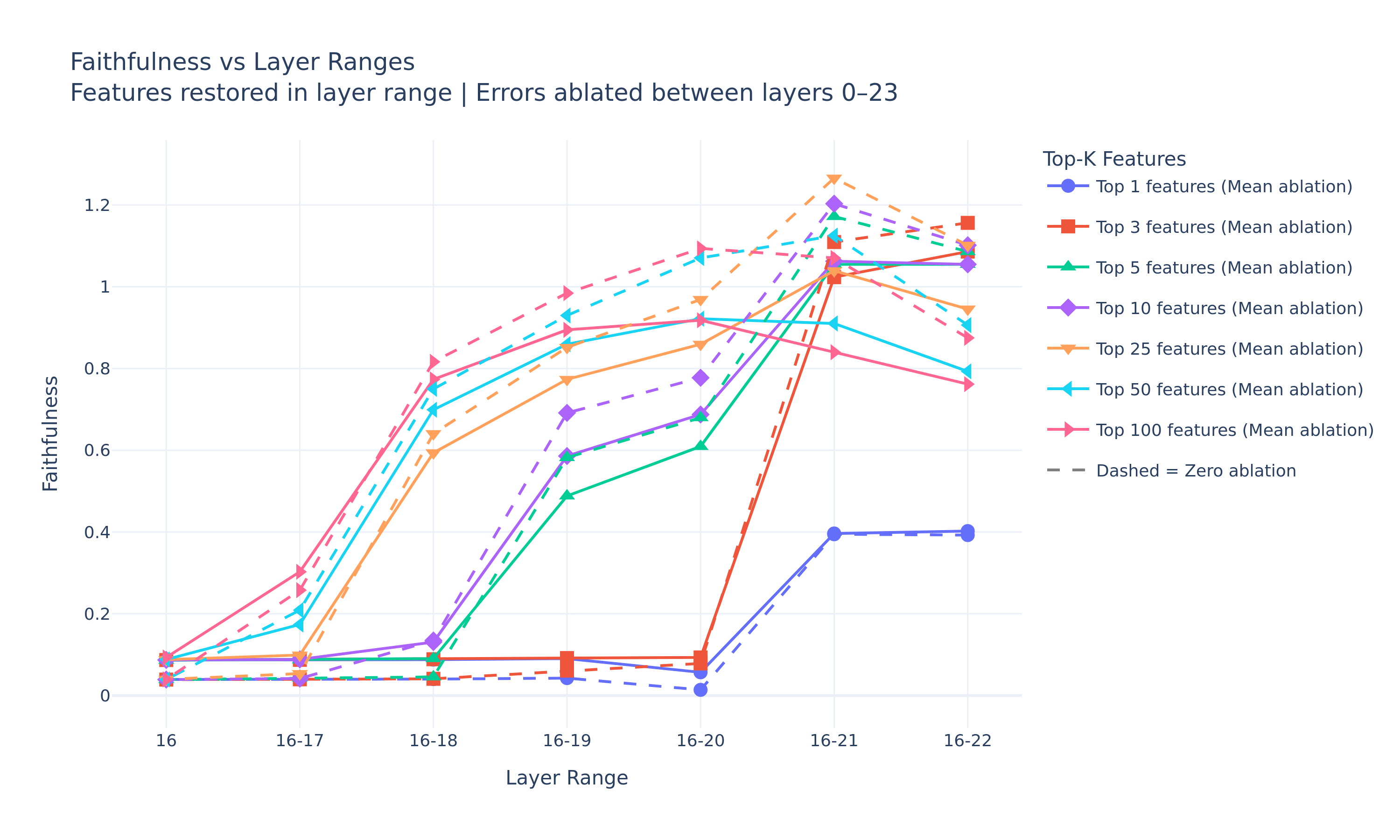
And this was quite counter-intuitive to us, given that zero ablation should throw the model out of distribution to a greater extent than mean ablation. Yet somehow, the model performs better in this case when we restore its top-K features, achieving faithfulness of 1.0 already in layers 16-19 with K = 100.
Ablation heatmap
For completeness (and to make our choice of not ablating the last two error nodes less arbitrary), we repeat a version of this experiment for different values of the ablation error threshold. That is, in our next experiment we stop ablating the error nodes not only at the last two layers, but also at the last one, last three and so on. We plot it using the following threshold notion: let’s call the ablation error threshold . Then, we don’t ablate all the error nodes at layers strictly greater than . Note that the error nodes with are not restored (back to their original activations), they are just not ablated (i.e. they still experience “ablation effects” of previous error nodes).
In the figure below, we show different values on the y-axis, and the x-axis stays the same – different layer ranges to restore the features from. We restore the top 25 features from each layer (as 25 seemed like a reasonable middle value from our previous experiment), and use mean ablation of the error nodes. This results in the following heatmap:
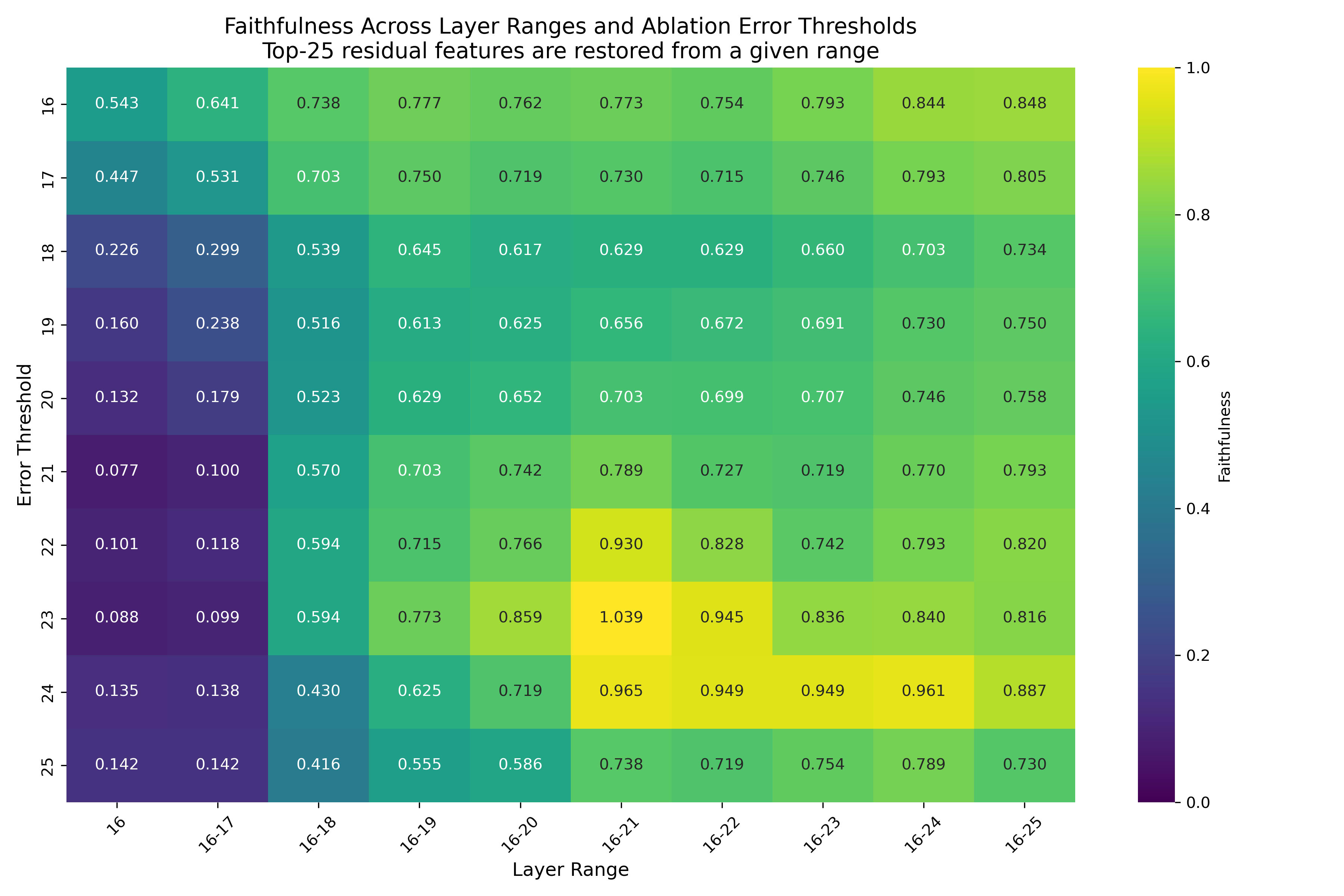
This is quite a big heatmap to parse, but upon closer look it contains many regularities, which we articulate below:
- Not ablating the last two error nodes ( ) is the most beneficial scenario, where our restoration procedure shows the best results.
- For nearly all error thresholds, there’s no gain from restoring nodes from layers beyond 18–21 [10].
- There’s also a significant effect in restoring features from layers 16-17, but only when .
- Contrary to the intuitive expectation that “the fewer error nodes we ablate, the better”, this isn’t quite the case. Looking at the row, we actually see that as we ablate fewer error nodes (move upward in the heatmap), faithfulness decreases—down to a minimum around . It seems that mean-ablating error nodes with low scores (which is what we have between layers 19 and 23) can actually help performance when we restore the top 25 features across most layer ranges.
Let’s also analyze the impact of the last two error nodes using this heatmap. Because we will refer to the same circuit visualization from the SFC paper we used above, we duplicate it below with a new annotation for reading convenience.
- Comparing the row corresponding to (when only the last error node is not ablated) and 23 (last two nodes are not ablated), we can see that the impact of the layer-24 error node strongly depends on the layer range from which we restore features:
- For ranges up until layer 20, we’re significantly losing faithfulness (if we ablate layer-24 error node)
- Consistently with the first experiment, restoring layer 21 yields the best faithfulness boost, restoring it to 1 even when we ablate the layer-24 error node
- The last error node appears to be particularly important, and no layer range seems to contain features whose restoration can mitigate the effect of ablating it.
We highlight this layer-24 error node because of its unusual role in the circuit: it’s the only error node whose patching effect (and corresponding AtP score) is negative—meaning that patching it actually harms the model’s ability to predict the correct verb form. At the same time, it receives two very strong incoming edges, with some of the highest edge weights in the circuit. In other words, the two upstream features have a strong positive influence on this error node—patching their values changes the error node’s value in a way that greatly improves the performance [11].
All of this is pretty weird—and our main takeaway is that the error nodes in the last two layers respond quite differently to our feature restoration intervention. Combined with their differing AtP signs and incoming edge activity, this suggests they may be playing very different roles in the circuit.
Alternative interpretations
Now it’s a good time to mention all alternative hypotheses that we have in mind. But first, let’s update on our main cross-layer superposition hypothesis. The results we obtained are consistent with the possibility that a sizable set of features in layers 18 and 19 are represented in cross-layer superposition (when we restore the top-25 of them, the faithfulness goes up from 0.13 to 0.75-0.85 depending on the ablation variant). Yet, this is not the full restoration that we had hoped for, leading us to the following alternatives.
Intermediate features hypothesis is probably the elephant in the room here – a possibility that our error nodes may contain other features not captured by the SAE. This could explain both the observed restoration effect (since intermediate features may causally influence the ones we do restore) and its limitations—because those intermediate features may continue to drive downstream behavior through paths we’re not touching when we only intervene on SAE-recovered features. This idea was roughly illustrated in the second figure at the start of this section, where we speculated about two active paths stemming from upstream error nodes (before layer 18): one passing through the downstream error nodes, and the other through the SAE features.
What is unsatisfying to us about this hypothesis is that it’s boring it seems weirdly pathologic if we consider how the error nodes are connected via the edge weights in the early layers. For easier reference, we duplicate the first part of the circuit (last token part) below.
Tracing the error nodes' (triangles) incoming/outgoing edge weights (blue arrows), we can notice how consistently they connect the error nodes, but not the other features. This may be visual overfitting, but it’s strange to us why they are connected so much better than the corresponding SAE nodes from the same layers. It’s as if they share some common structure, some duplicate features that trivially influence each other by the relationship [12]. And if they do contain duplicate features, why are those features consistently not captured by like 12 SAEs in a row? After all, verb agreement is such a common task (even across relative clauses) that they shouldn’t be as difficult to pick up as the much more sparse abstract concepts [13].
What seems a bit more likely to us is a similar-but-not-quite redundant features hypothesis. It’s motivated by the wide belief in today’s mech interp that in large models, “there is never a single reason/mechanism for why the model does a particular thing” (e.g., see this post). Training is probably an extremely messy and chaotic process, when multiple identical/closely similar mechanisms can arise in parallel ala induction heads, some mechanisms can be suppressed by the newer ones (as in grokking) etc. We hypothesize that something similar might be happening here: the error nodes could contain older, rudimentary features that were "pushed aside" by more salient ones that developed later in training. But as long as these earlier features aren’t actively harmful, the model may still retain and use them—alongside the "main path" built from the more prominent SAE features.
One piece of evidence against this hypothesis, though, is that ablating the error nodes seems to have too strong of an effect for something that would just be a “side mechanism”. We explore this in more detail in the “Targeted Error Ablation” section.
Regarding our original cross-layer superposition hypothesis, it obviously had to be updated:
- Restoring layer 19 features is also crucial for the model’s performance, which suggests that layer 19 may also contain features in cross-layer superposition (perhaps the layer-18 error node might be entangled in this since it has second-highest AtP score among error nodes).
- Most likely, there is more than 1 feature represented in cross-layer superposition.
- From the zero ablation & restoration plot above, we also interpret layer 21 as a kind of “checkpoint” - restoring the features from it is sufficient to fully restore the model’s performance—even with as few as the top 3 features. But it’s not necessary - if we restore enough features from previous layers (19 and/or 20), the performance is also almost recovered.
The results also indicated to us that even if the hypothesis is true, it likely doesn’t explain all of the error nodes’ functionality in our circuit (last error node being important etc.), and the best thing we can hope to say is “it explains most of it”.
Targeted error ablation
The motivation behind this line of investigation is that we don’t really know what the baseline ablation effect represents when we ablate all residual error nodes. It’s possible that this effect is driven by a small, critical subset of nodes, while the rest contribute little or nothing. So, the goal of this section is to try to narrow down which error nodes have the most significant impact when ablated.
Sliding window ablation
We start with a so-called sliding window experiment. As before, we’ll mean-ablate error nodes, but this time we’ll do it
- Within a sliding window covering the layer ranges, starting from layer 0 to 3, then from 1 to 4 and so on.
- We won’t restore any features or other nodes
The resulting plot shows the faithfulness of the ablated model for each sliding window range, with error bars indicating the standard deviation across samples:
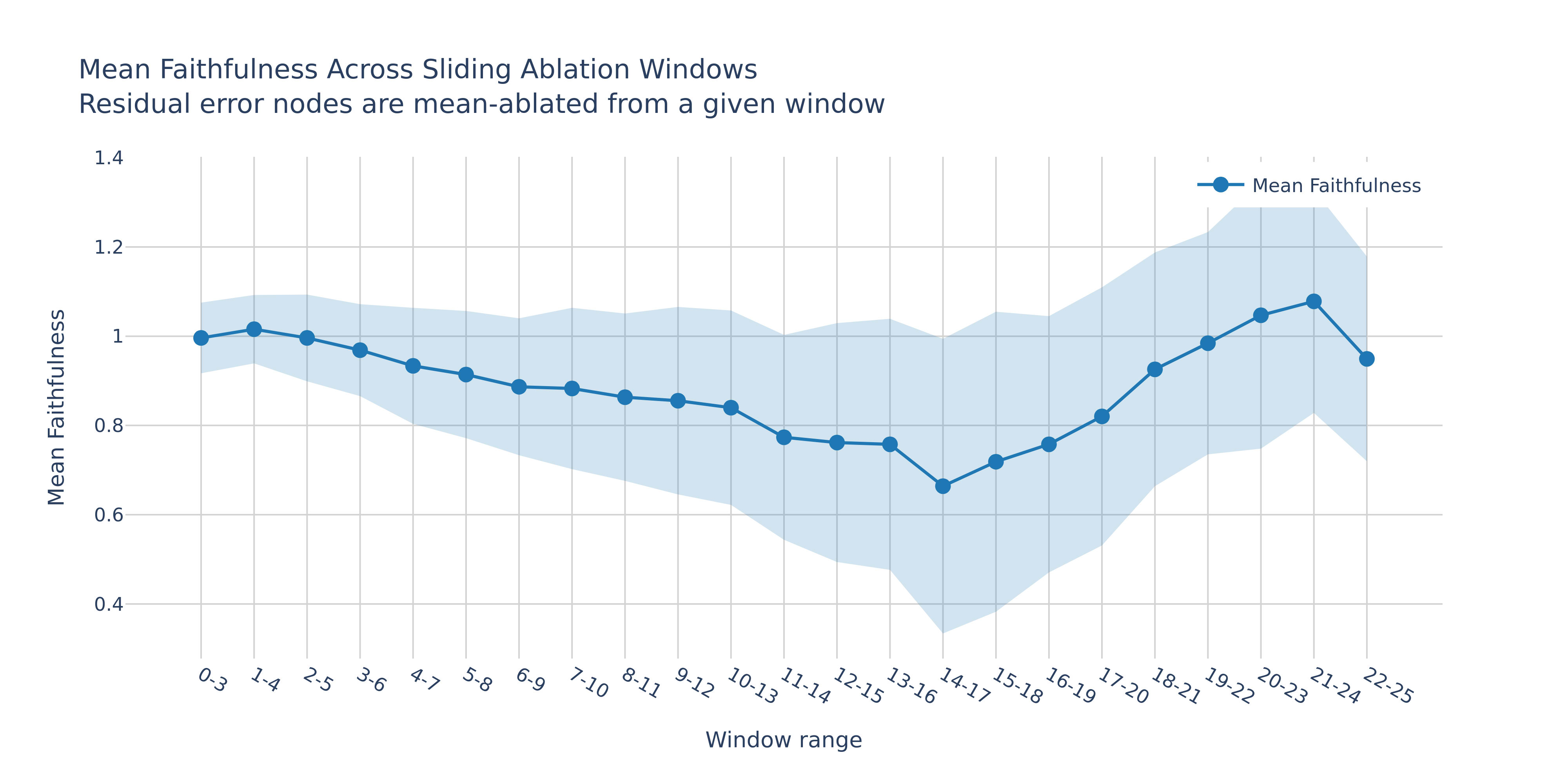
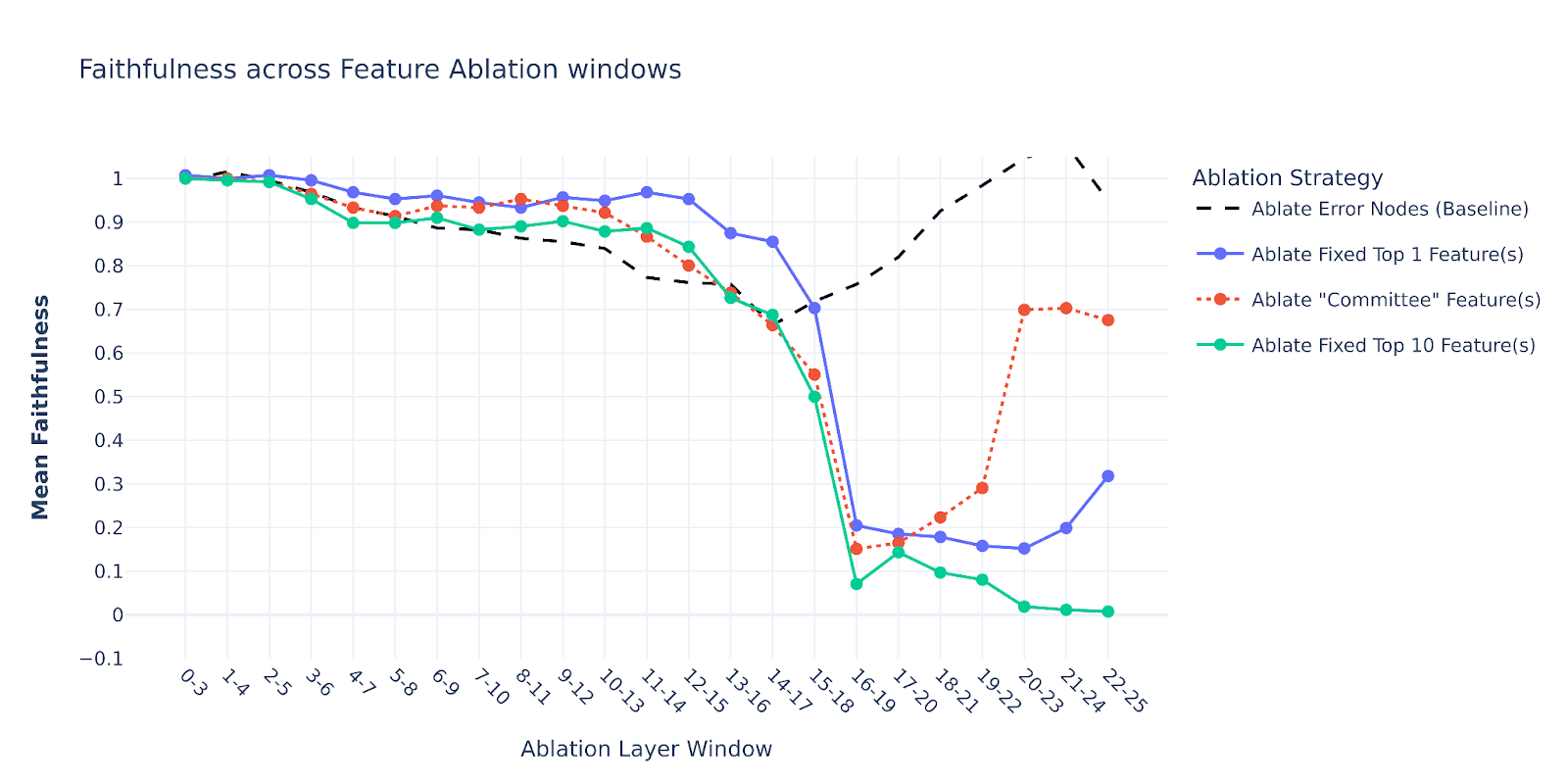
- Consistently with error nodes AtP scores, the most critical layer range is 14-17 – ablating error nodes from those layers has the biggest ablation effect. Also, we see a significant drop when layer 14 is entering the sliding window, and an increase when layer 17 is leaving it.
- Interestingly, ablating ranges starting from layer 18 (18-21, …, 22-25) has very little effect on the resulting faithfulness. This might be a rough piece of evidence against the alternative “path through the error nodes”
[this is only rough evidence because in ablation experiments one always has to keep in mind the Hydra effect a.k.a. self-repair, when some model components can make up for the ablation effect of the other components, downweighting the ablation scores that we see]
Initially, we thought that such a small ablation effect in early layer ranges (say, before layer 10, when faithfulness in the mean-ablated variant is between 0.8 and 1) is also quite suspicious. So, we decided to test this against a feature baseline - perform the same experiment, but ablating a selection of features from a given ablation range instead of the error nodes. We implemented the following baselines variants:
- Top-1 Feature: For each layer within the ablation window, we select a single last-token SAE with the highest AtP score at that layer and token.
- Top-10 Features: same as above, but with 10 top features.
- Features “Committee”: from each layer, select a specific group of features that most closely match the error node's AtP score at that layer but also exceeds it.
- If there are features whose AtP score is larger than the respective error node’s score, choose the one that is “the closest” to the error node’s score.
- Otherwise, select as many top features as it takes before exceeding the error node’s score.
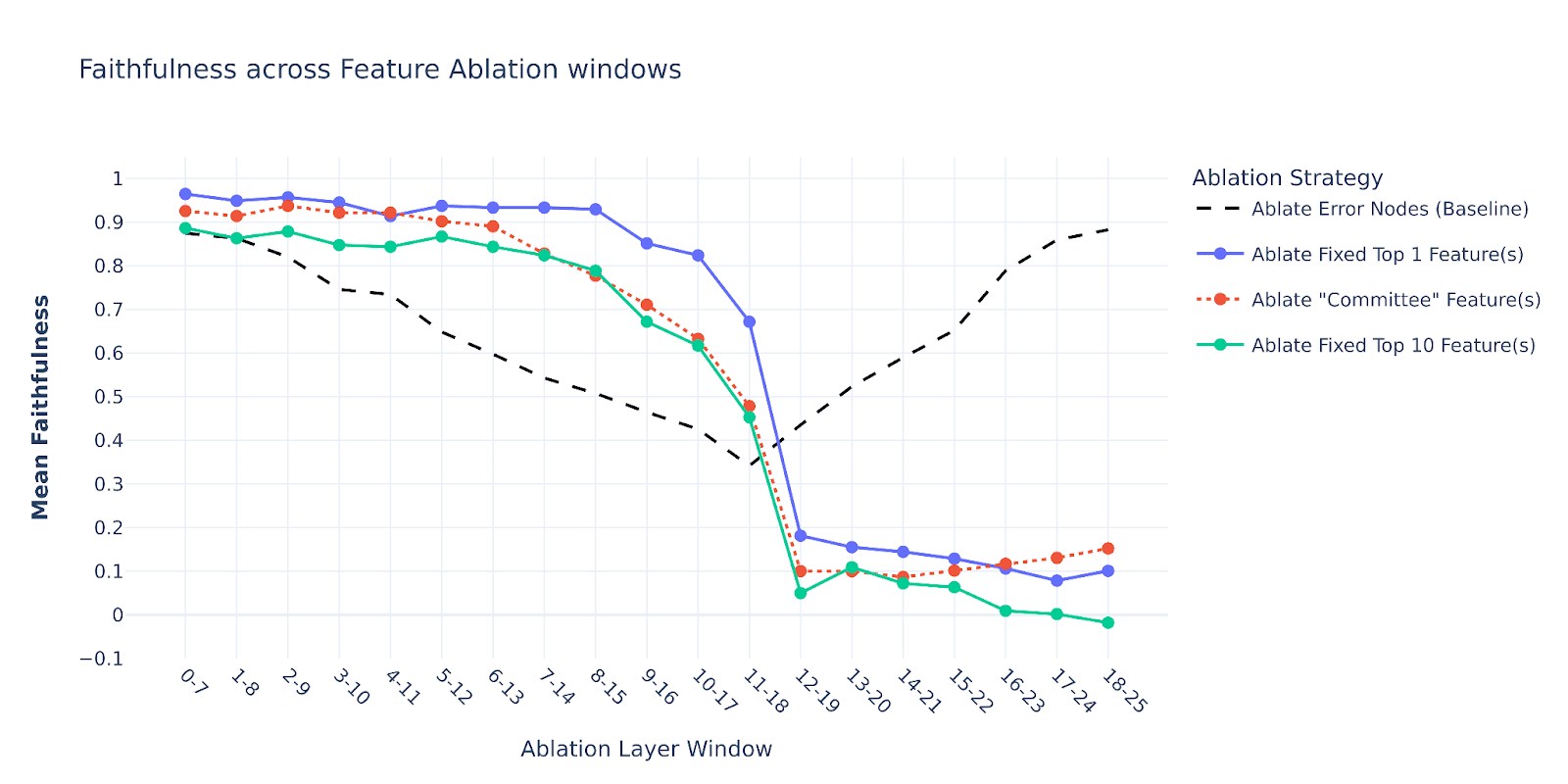
We plot each baseline below for all layer ranges we previously considered. The error nodes ablation variant (from the previous plot) is also shown as a dotted black line.
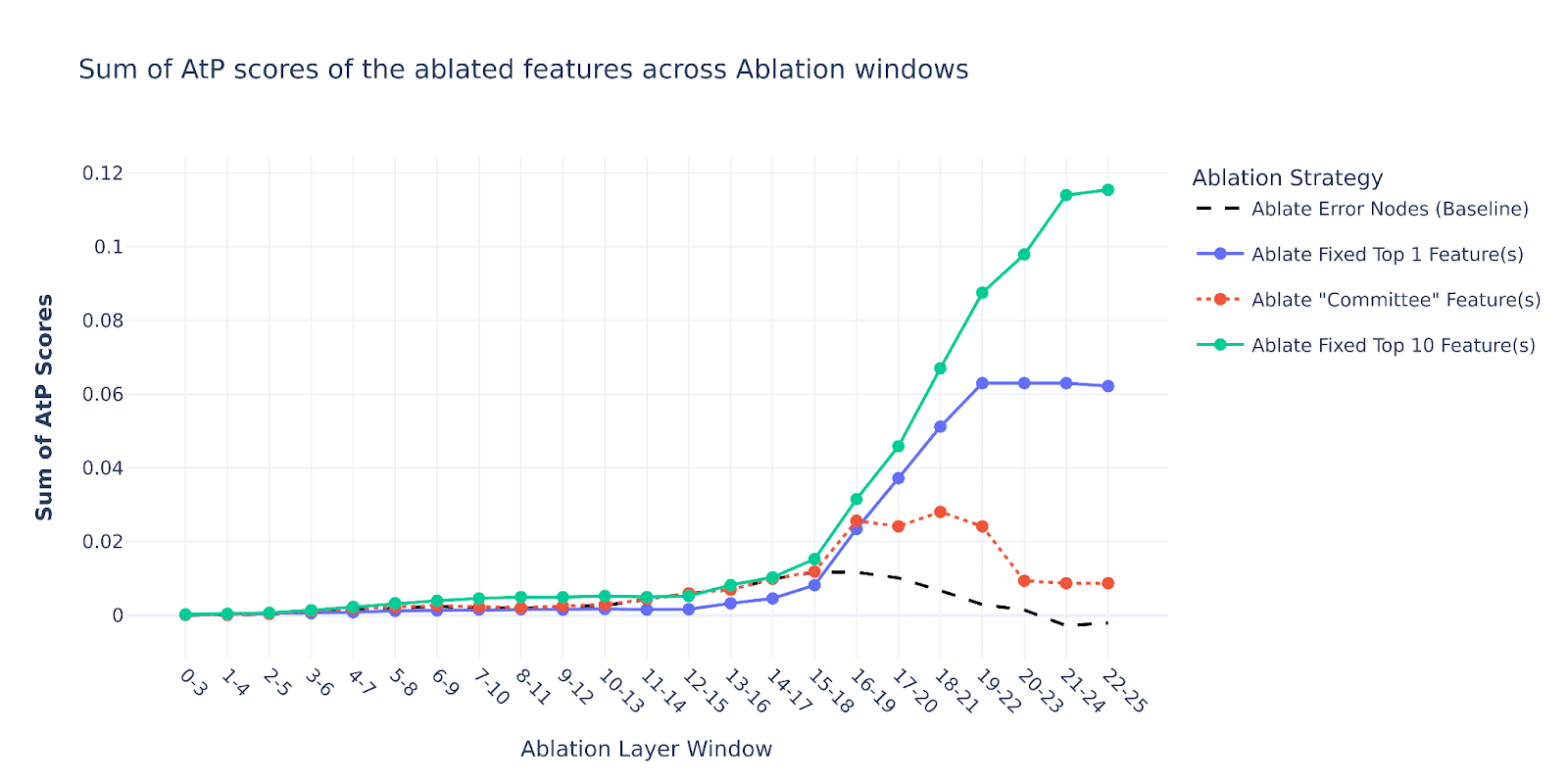
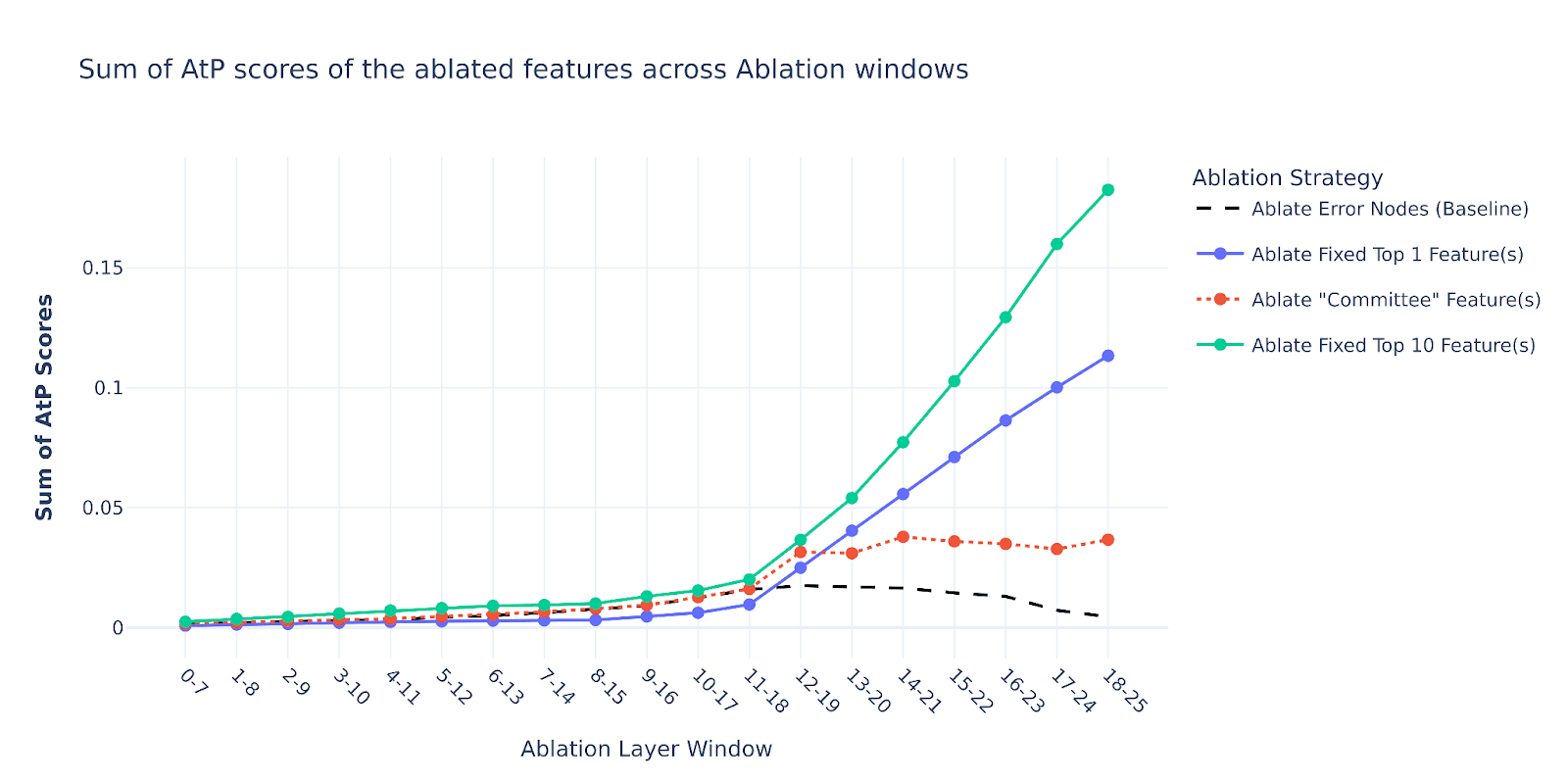
And so, it seems that there is nothing unique about the mild ablation effect of adjacent nodes - for early-mid layers, it stays above 0.7 for both error nodes and feature nodes ablations. In fact, ablating contiguous SAE node segments with a similar AtP score appears to hurt the model’s performance less than ablating the error nodes in early-mid layers. And then, all our feature baselines seem to destroy the model performance in late layers, but that’s quite expected since they have much higher total AtP scores as shown in the below plot.
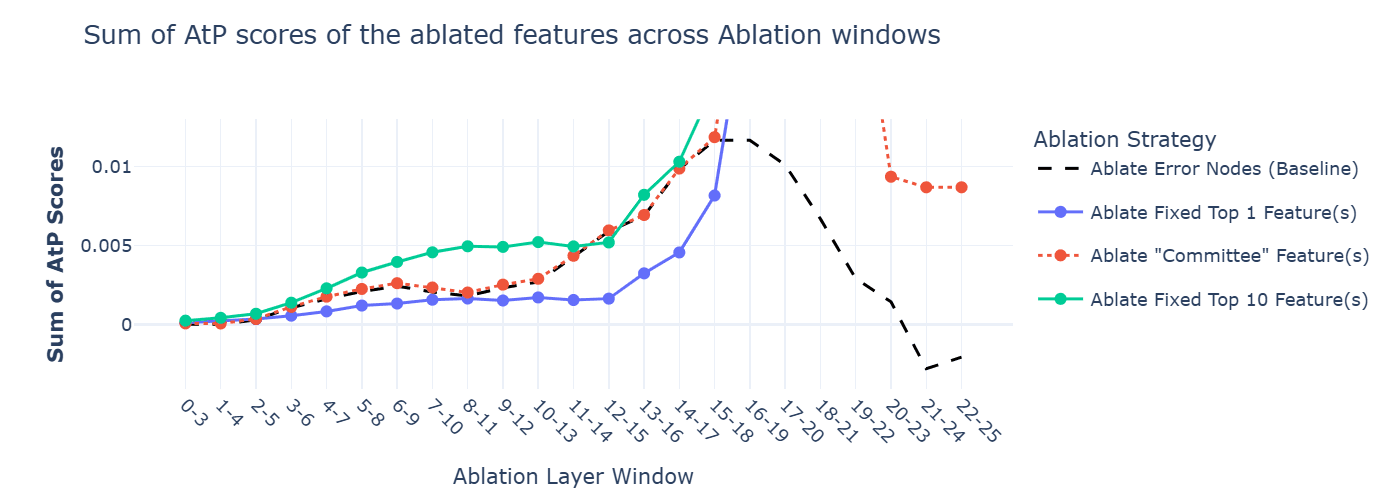
Here is also a zoomed-in version of this plot, showing that our “Committee” baseline quite tightly bounds the error nodes’ AtP score from above for early-mid layers.
What about the zero ablation variant? The intuition we have here is that mean ablation still allows the model to access some task specific information: for example, features that always active in our simple sentences with relative clauses (e.g. the third token is always a noun) will have the average value roughly equal to their values at any specific prompt, so mean-ablating them shouldn’t do anything. In contrast, zero ablating such features should throw the model out of distribution and hence be much more destructive.
The similar intuition can be applied to error nodes: if our hypothesis is true and they contain some internal variables used for computing the later features, then the more task-specific those variables are, the bigger will be their zero ablation effect as compared to mean ablation. So, we hoped to understand how task specific vs prompt specific our error nodes are by checking how much their ablation effect when we use zero ablation vs mean ablation [14].
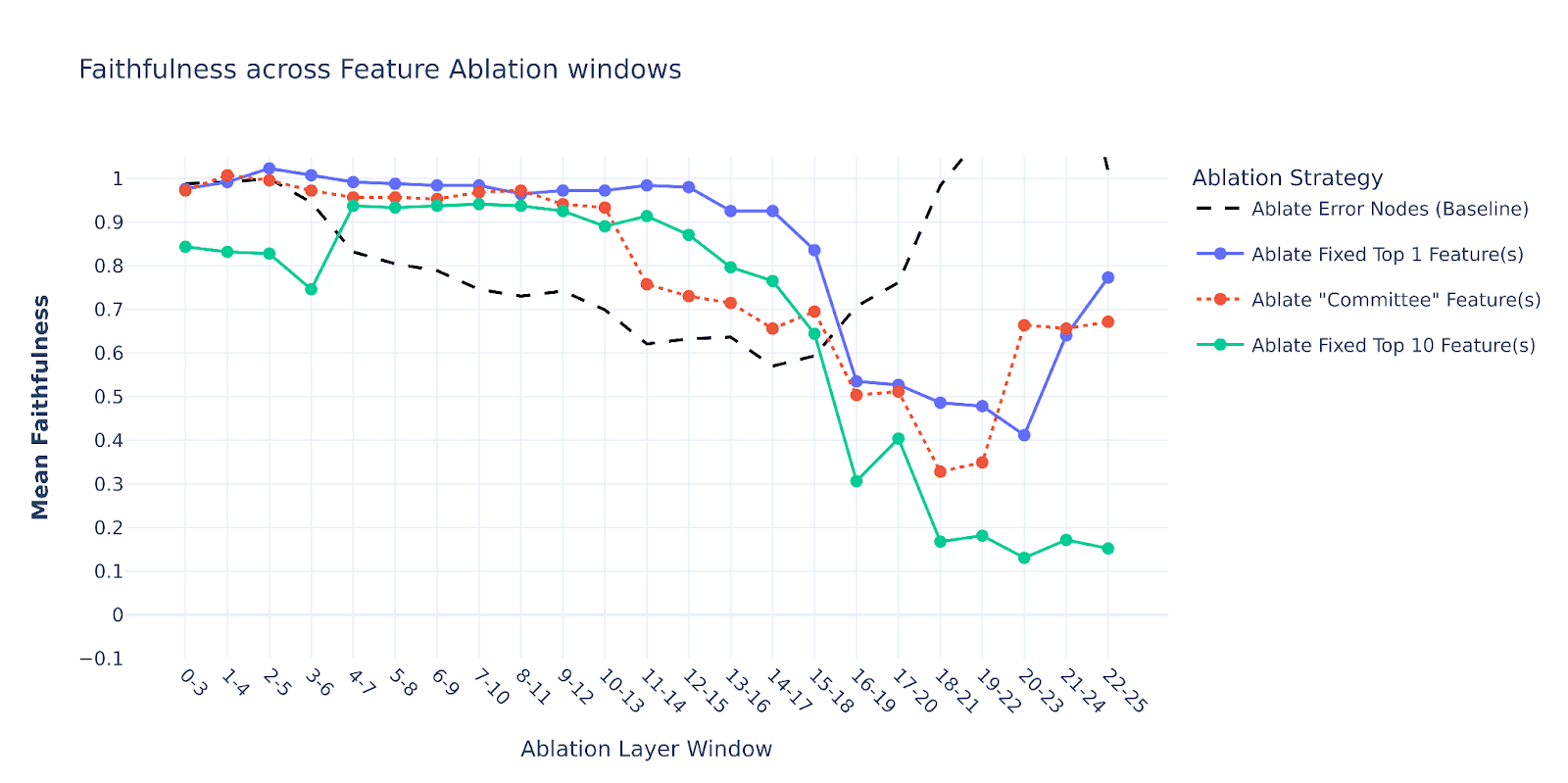
The zero-ablation variant of the above experiment is given below.
Interestingly, ablating the error nodes here leads to a sharper decline in faithfulness (compared to the mean ablation) than ablating the feature nodes, which doesn’t seem to have a big difference between two ablation scenarios. To make it visually clearer, we computed the differences between the 1st plot (mean ablation variant) and the 2nd plot from above (zero ablation variant) and plotted them below:
This may serve as rough evidence that the information contained in the error nodes is more “task-specific”, since mean ablating them causes a milder drop in faithfulness compared to the feature nodes.
To wrap this section up, we also present a similar plot for sliding window size of 8 and mean ablation of the error nodes:
The error nodes didn’t seem to like that! The plot suggests that ablating contiguous error node ranges with range size as large as 8 is significantly more destructive than ablating our feature nodes, even when the feature nodes have a larger total AtP score (“Top-10” baseline):
The problem remains the same: we would like to claim that these results suggest our error nodes behave qualitatively differently from feature nodes—but given how noisy the ablation effects are, this isn’t strong enough evidence. On top of that, we’re not sure how meaningful our feature baselines are, since A) there don’t seem to be enough important last-token features in the early-to-mid layers B) ablating SAE nodes and error nodes is conceptually different. A proper baseline would be error nodes that are composed of known SAE features—but unfortunately, we don’t have that at our disposal.
Expanding window ablation
This last subsection is aimed to answer the natural follow-up question: “if ablating contiguous ranges of error nodes only has a moderate partial effect, when will we observe the full ablation effect with faithfulness dropping down to zero?” In other words, how much should we ablate the error nodes to destroy the model’s performance?
Sliding right boundary
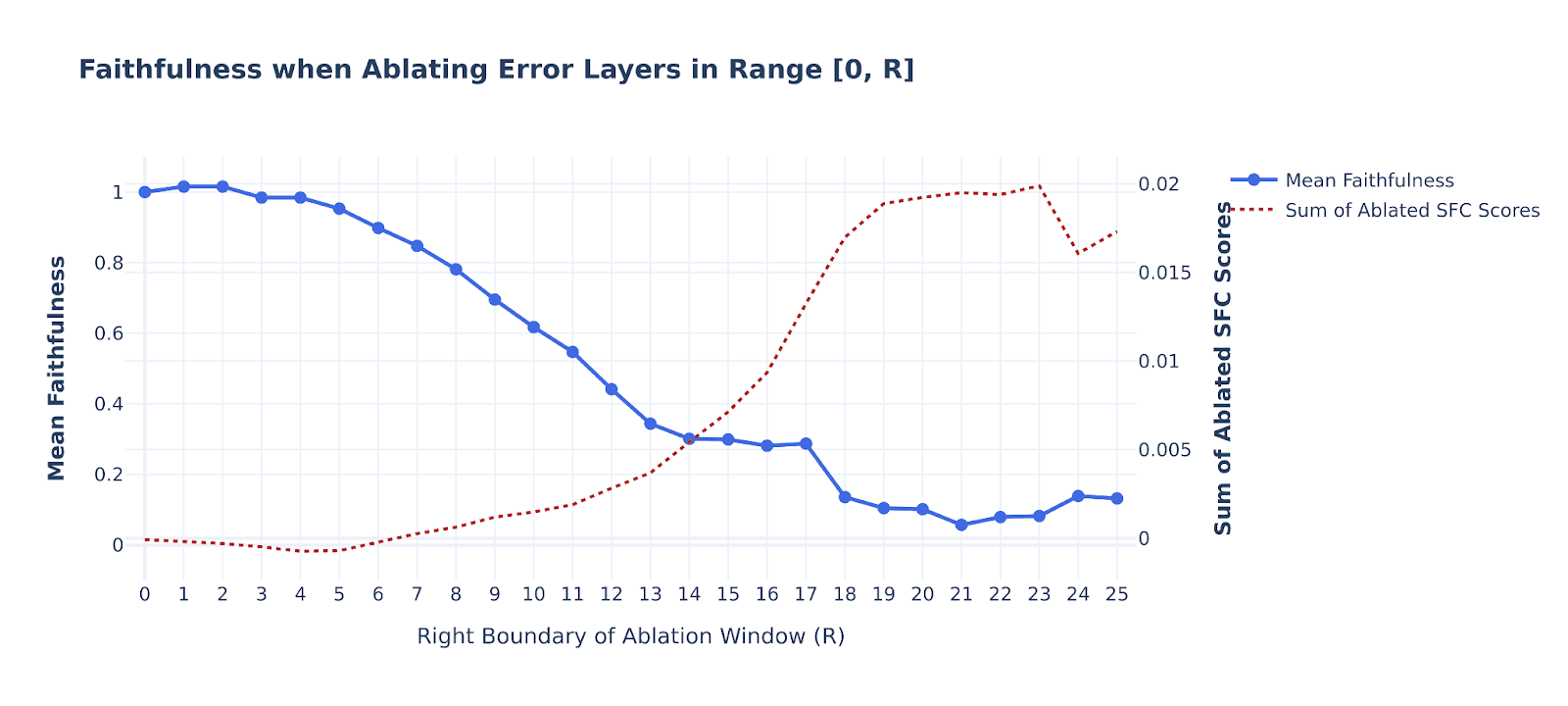
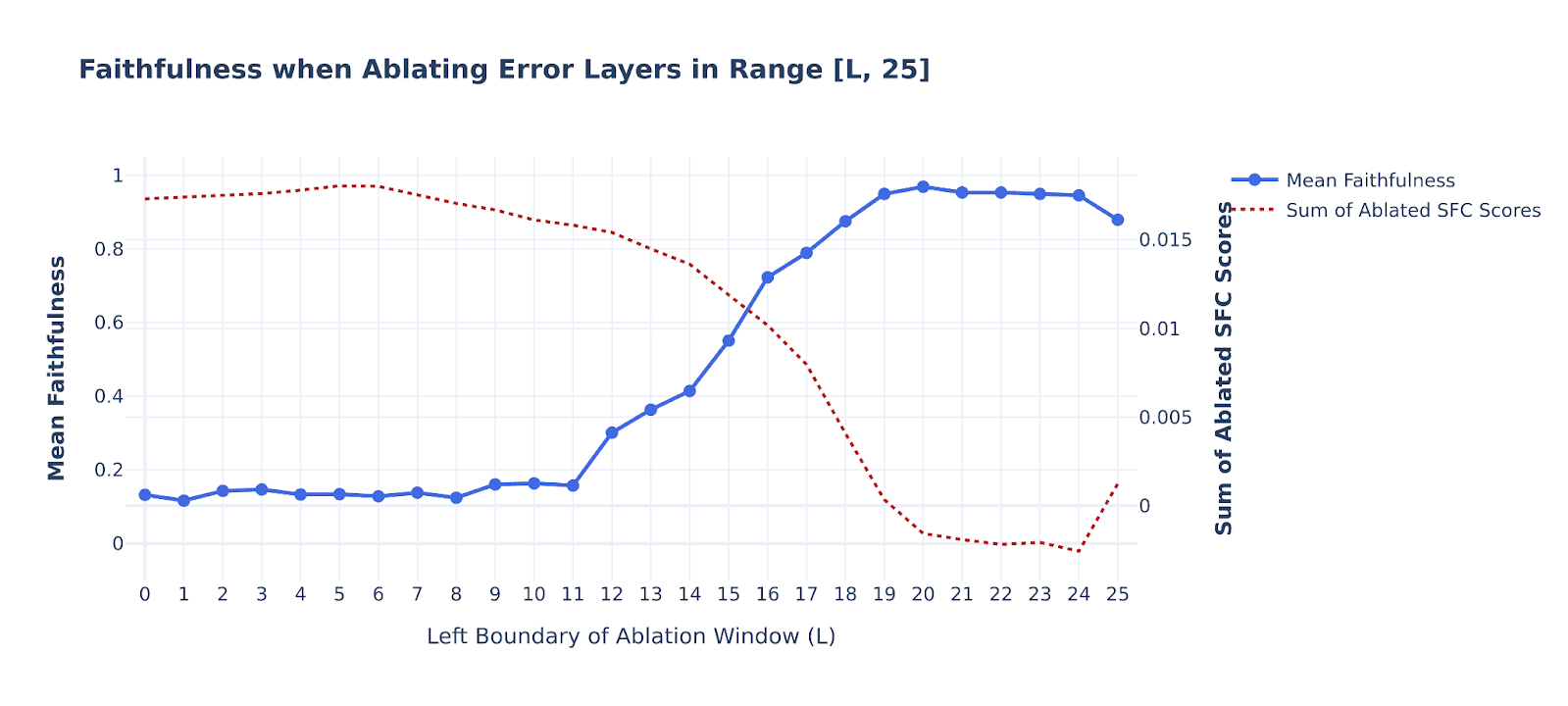
We perform the variation of our sliding window experiment, but here instead of sliding the entire window, varying the left and right bounds at the same time, we only slide the right bound while keeping the left one fixed at 0 (i.e. at the 1st layer). Using the mean ablation variant, this results in the following plot:
The red dotted line marks the cumulative AtP scores of the error nodes within the given range. As we can see, the decrease is quite gradual (except for the layer 18) and reaches zero only in late layer ranges.
Sliding left boundary
Similarly, we conduct a similar experiment when the right bound is fixed at the maximum layer 25, and the left one varies up to 0.
Note that here the “orientation” is reversed: x = 0 point in the plot corresponds to the maximum ablation range, and as x increases, fewer and fewer nodes are ablated which increases faithfulness.
Taken together with the previous plot and the sliding window ablation results (using a window size of 8), the findings consistently point to the 11–18 layer range as the critical region for our error nodes—ablating this range leads to the most significant drop in model performance down to the faithfulness score of 0.3.
Conclusions
While drawing any definite conclusions from ablation-based experiment is conceptually difficult due to the Hydra effect (self-repair) as mentioned above, we still think that our results somewhat lower the probability of the alternative “path through the error nodes” hypothesis:
- Ablating late error nodes alone has almost no effect on the model’s performance, while ablating late SAE features does.
- Error nodes behave qualitatively differently when ablated than SAE features, but it’s not clear whether it suggests that the error nodes are not composed of features, or that the features baselines we selected are flawed.
- We’ve also become a bit more confident in what error node range is most critical for the model’s performance (layers 11-18).
Reproducibility
Our Github repository is available at https://github.com/ambitious-mechinterp/SFC-errors
Future work
- Refined causal investigations: to answer questions like “what error nodes influence the most in our circuit” we could apply more extensive gradient attribution techniques. To the best of our knowledge, current edge attribution technique by Marks et al. has only been applied to intermediate neighbouring nodes, while for our purposes it might be more beneficial to trace the error nodes effect (say, from the critical range of layers 11-18) to other downstream nodes (although some significant optimizations might be required to do this efficiently).
- Be smarter about which latents to restore: currently to restore features we use a very rough heuristics of restoring top-K latents by AtP scores from each layer. But if our goal is to find specific features that are “good candidates of being represented in cross-layer superposition” to inform further experiments, we probably can do much better by specifically searching for features, restoring which yields the highest faithfulness boost when error nodes are ablated. One example we have in mind is to adopt one of binary mask optimization techniques, like the ones that were previously employed as an alternative to circuit node identification by Caples et al.
- Acausal Crosscoder analysis: the one we unsuccessfully attempted to perform ourselves, as detailed in the next section.
Acausal crosscoder analysis
TL;DR: We hoped to train BatchTopK acausal crosscoders to capture the representation of features in different layers. This would allow us to A) analyze how our SVA features are distributed across layers (provided that we can match SAE- and crosscoder-features); and B) do a gradient pursuit directly on the crosscoder decoder directions and use that in lieu of SAEs, and see if that reduces the reliance on error nodes in this circuit.
However, our crosscoders had a large number of dead features and the overall training curves were unpromising for the hyperparameters & training modifications we tried. Below are the motivation behind this direction and what we would’ve done given more time to solve the training issues.
Background
One way to reveal cross-layer superposition is to train acausal acrosscoders. The acausal crosscoders we use consist of one pair of linear encoder and decoder per layer, and we train using layers X through Y. The encoded activations are summed across all N layers, passed through a BatchTopK/ReLU activation, and the single sparse activation vector is then passed to each layer’s decoder to reconstruct the activations at that layer. In other words, for any input token x, call the activation at layer l as al(x), the hidden activations of an acausal crosscoder is
Which are then decoded to approximations
By using a single shared hidden vector across all layers, acausal crosscoders aim to capture any feature that has appeared in any layer of the model and locate the (linear) representation of that feature across all layers it activates on.
Why might acausal crosscoders capture feature representations used by our LLMs that SAEs regulate to the error term? We already touched on this citing Anthropic's early experimental results (Error nodes as a result of cross-layer superposition section), but we’ll reiterate some reasons here.
Suppose some feature F canonically becomes most prominent at layer X (resid_post) can be calculated in two ways: a simple way that involves a single MLP in layer X, when the feature is very prominent, and a hard way of which involve multiple components contributing among layers X - 1, X - 2, and X - 3. The intermediate computation in layer X - 1, X - 2, and X - 3 might not be captured by an SAE.
However, if the feature F is sufficiently prominent and important to the model at least in a single layer, the acausal crosscoder will dedicate one slot in its hidden dimension to that feature F, and the various decoder and encoders at each layer should attempt to “find” a representation of feature F at that layer, which would include intermediate computations in layers X - 1, X - 2, X - 3. In other words, the training process & the architecture of the acausal crosscoder encourages it to capture feature representations in different layers.
In the original post, Lindsey et al. studied latent formation through a model by looking at the relative norm of a latent’s decoder norm at each layer. The idea is to use the norm of the decoder direction as a measure of how “active” a latent is at a given layer.
However, this is a static analysis that captures some sort of average across the entire dataset: because a single latent’s activation is the result of a sum across encoders in all layers, the relative activation of a latent on some input in the crosscoders’ activation reconstruction is fixed for any specific input. In our earlier example with feature F, this means that the way the feature F is reconstructed in layers X - 3 through X is the same regardless of which mechanism is active.
To circumvent this issue, we hoped to apply inference time optimization techniques directly on the crosscoder decoder weights. Instead of using the encoders from all layers to determine which latent is active at a given layer and by how much, we use gradient pursuit directly on the decoder weights. Gradient pursuit takes in our trained dictionary and greedily finds a k-sparse reconstruction of our activations using dictionary latents.
Training crosscoders and issues
We adopted Oli Clive-Griffen’s codebase for training BatchTopK acausal crosscoders. The main changes that actually mattered were implementing a large, shuffled activations buffer and tweaking auxiliary loss hyperparameters. Other changes included improved activations harvesting: removing high norm activations, implementing padding etc.
However, we were unable to get the reconstruction loss curves we wanted (although it’s possible that we’ve done the best we can). You can find our training code here, our wandb project here, and a discussion on the open source mech interp slack here. The next idea we would’ve wanted to try is starting with a much larger k (e.g., 1200 instead of 120) for the batch top k activation and slowly decreasing it over time (credit to Nathan Hu on slack for the idea).
Concrete MVE for tackling the cross-layer superposition hypothesis
And finally, this is the main section where we lay out our specific proposal for how we believe this project should move forward—leveraging acausal crosscoders.
- Having trained a Gemma-2 acausal crosscoder that contains our critical 11-19 layer range, identify its latents that have the highest activation/cosine similarity to our top scoring SAE latents (by AtP score)
- We would start with searching for latents whose decoder norm peaks at layers 18-19, which we hypothesize to contain the best candidates for features represented in cross-layer superposition.
- Having identified the relevant crosscoder latents, check how their decoder norms are distributed across previous layers (before their peak), i.e., replicating Anthropic's figure above.
- If we find that these decoder norms closely correlate with AtP score of our error nodes, this could be a good piece of evidence for cross-layer superposition.
- Having kept only those latents that show high correlation of their decoder norms with error node AtP scores, try to restore only those latents and see if it mitigates the ablation effect of our error nodes with greater effectiveness than the coarse top-K restoration procedure we employed.
SAE error probing
TL;DR:
When training linear probes, consider using logistic regression with l2 penalty instead of using AdamW/other SGD methods on the dataset. If you do use SGD, tune your hyperparameters. I thought training probes on the SAE error term leads to slightly more accurate probes compared to the residual stream when using AdamW, but this is likely due to bad hyperparameters. When we train probes with logistic regression, we get better results across the board and probing on the residual stream leads to the best performance.
(Some of the results here were also used as my (Tim Hua)’s MATS application for Neel Nanda’s stream. Code for the initial AdamW results can be found here, and code for the logistic probing and experiment three can be found here. These aren't really cleaned up.)
Intro and motivation
Previously, we considered cross-layer superposition as a possible explanation for error nodes in circuits. We attempted to study one specific instance of cross-layer superposition in the subject verb agreement across a relative clause circuit in Gemma-2 2B. Now, we’ll consider another case of what could be inside the error node: directions containing arbitrary boolean functions of features.
In the mathematical framework for computation in superposition, Hänni et al. show that an MLP with random weights can calculate AND between arbitrary latents and store the result in an linear direction that is epsilon-orthogonal between the two original feature directions. In other words, it seems likely that large transformer models contain linear directions that represent arbitrary boolean functions of latents (see e.g., arbitrary XORs).
I suspect these arbitrary boolean function directions will be extremely sparse and not captured by an SAE, yet still useful to model computation. Perhaps we can partition the active latents in a model’s residual stream into “canonical latents,” which represent somewhat atomic features in the input, and “derived latents” which are directions representing arbitrary boolean functions between active and inactive latents. One possibility is that derived latents–which are low norm and high sparsity–always end up in the error term.
I ended up running a series of probing experiments. However, most of the initial linear probes were trained using AdamW with the default beta and weight decay parameters (0.9, 0.999, weight decay of 0.01). Anecdotally, AdamW trained probes are sensitive to activation norms (the SAE error term tends to have ~half the norm of the reconstruction or residual stream), and need some sort of hyperparameter sweep before I could find the absolute best performance. I later also trained probes using the logistic regression, which had better performance across the board compared to the AdamW probes. I haven’t had the time to really dig into this and figure things out, but I would be skeptical of all probing results from AdamW probes.
Experiment one: probing XORS in the error term
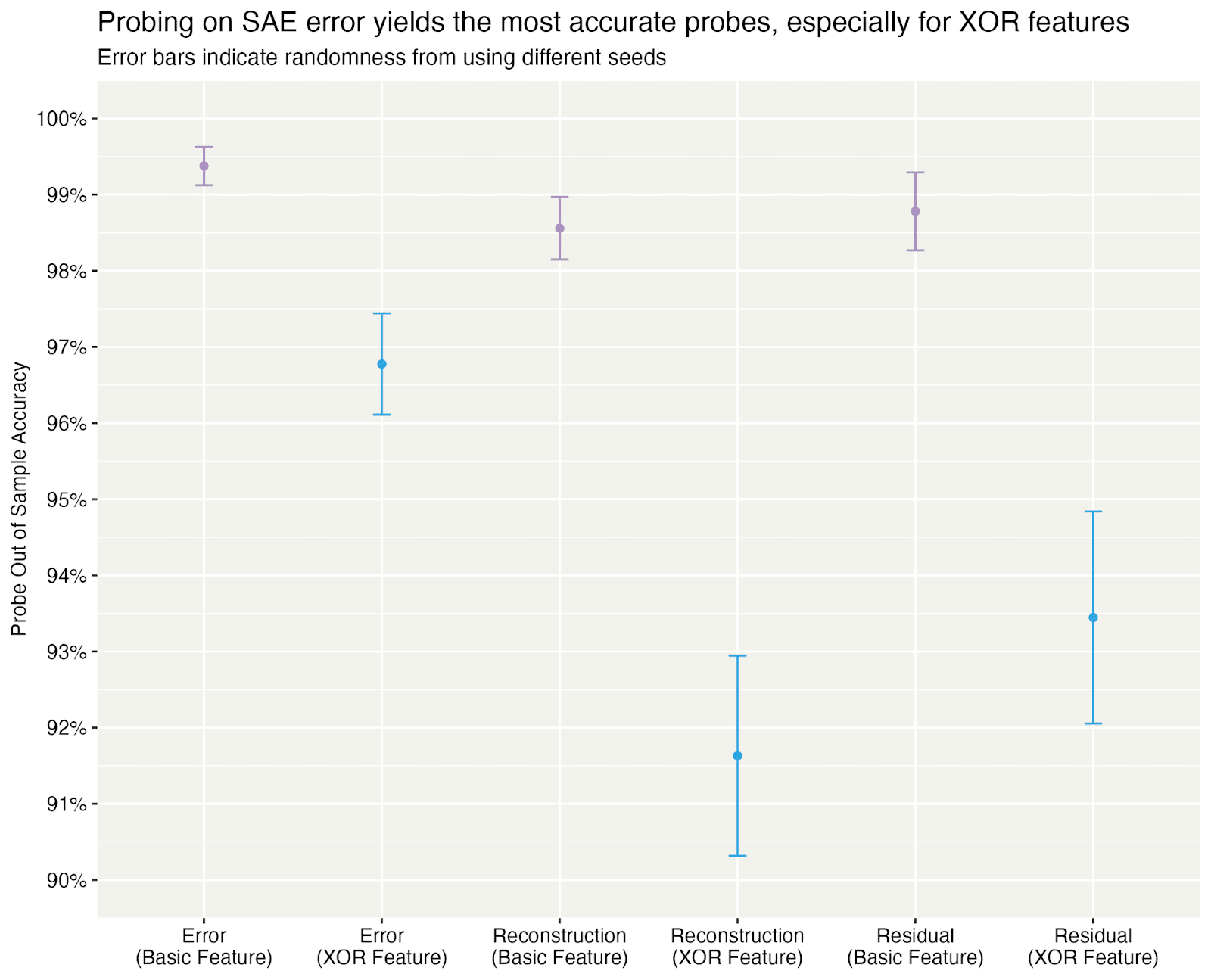
I thought that, since XORs are an example of a derived feature, and my hypothesis is that derived features live in the error term, I should be able to train probes for XOR on the error term and they’d outperform probes trained elsewhere. I trained linear probes (with bias) on the follow three sets of feature vectors:
- Residual stream of Gemma 2-2B at layer 19
- SAE reconstruction of the residual stream at layer 19, using the Gemma Scope SAE with width 16k and canonical l0.
- SAE error at layer 19 (i.e., residual stream - SAE reconstruction).
Following Marks 2024, I used statements from either “Bob” or “Alice” on cities and whether they belonged to a certain country. Here are a few examples from the data:
Bob: The city of Krasnodar is not in Russia
Alice: The city of Krasnodar is not in South Africa
Bob: The city of Baku is in Ukraine
Bob: The city of Baku is in Azerbaijan
Each statement has three “basic” boolean features we probe for
- Whether it’s from Alice
- Whether it contains the word “not”
- Whether it’s true
I also probe for the three possible pairwise XORs between these three features (e.g. Whether a sentence is from Alice XOR whether it’s true). These probes were trained using AdamW and I probe on the last token position.
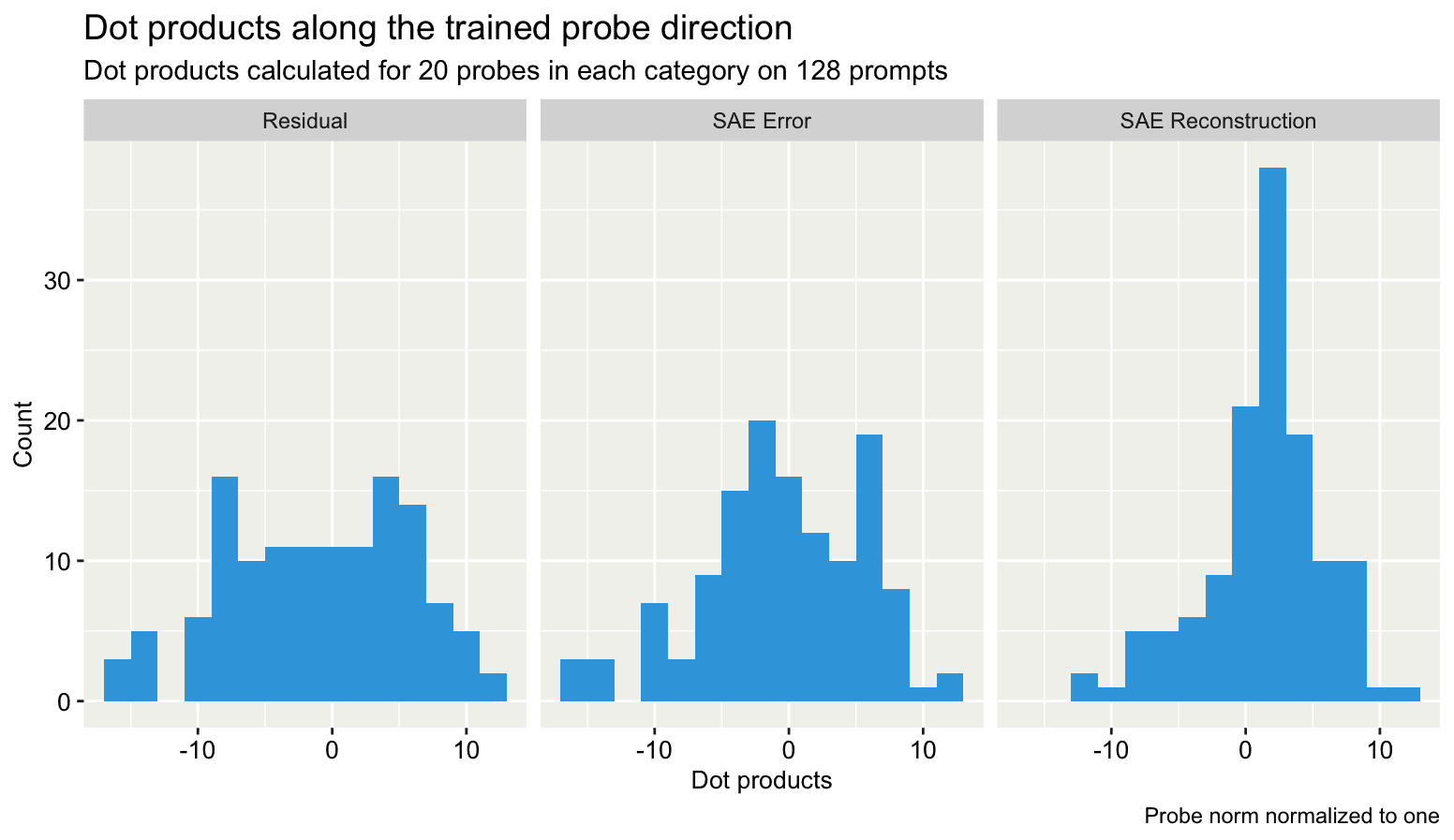
I do indeed find that you can probe for these random XORs, and they’re more recoverable in the SAE error than on the reconstruction. However, accuracy is also very high on the reconstruction–what gives? My best guess was that these derived features just live in various subspaces in the model, and the reconstruction space happened to be big enough to include these directions.
I mentioned some of these results to Sam Marks, and he proposed a much more simple and obvious explanation for my results: These arbitrary XORs are otherwise uninterpretable directions that make no sense, and thus the SAEs do not pick them up.
However, notice in the figure that even for basic features, the probes trained on the SAE error also had higher test accuracy compared to probes trained on the reconstruction and the residual stream. Could it be that the vast majority of SAE latents are usually not related to the specific concept, and thus the SAEs actually help us “de-noise” the residual stream, so that probing works better there? (Spoiler: Probably not, the discrepancies are likely due to using unoptimized AdamW hyperparameters. There might be some gains to ablating certain irrelevant directions, but they’re probably sufficiently small that it doesn’t really matter).
Experiment two: arbitrary probing on SAE errors
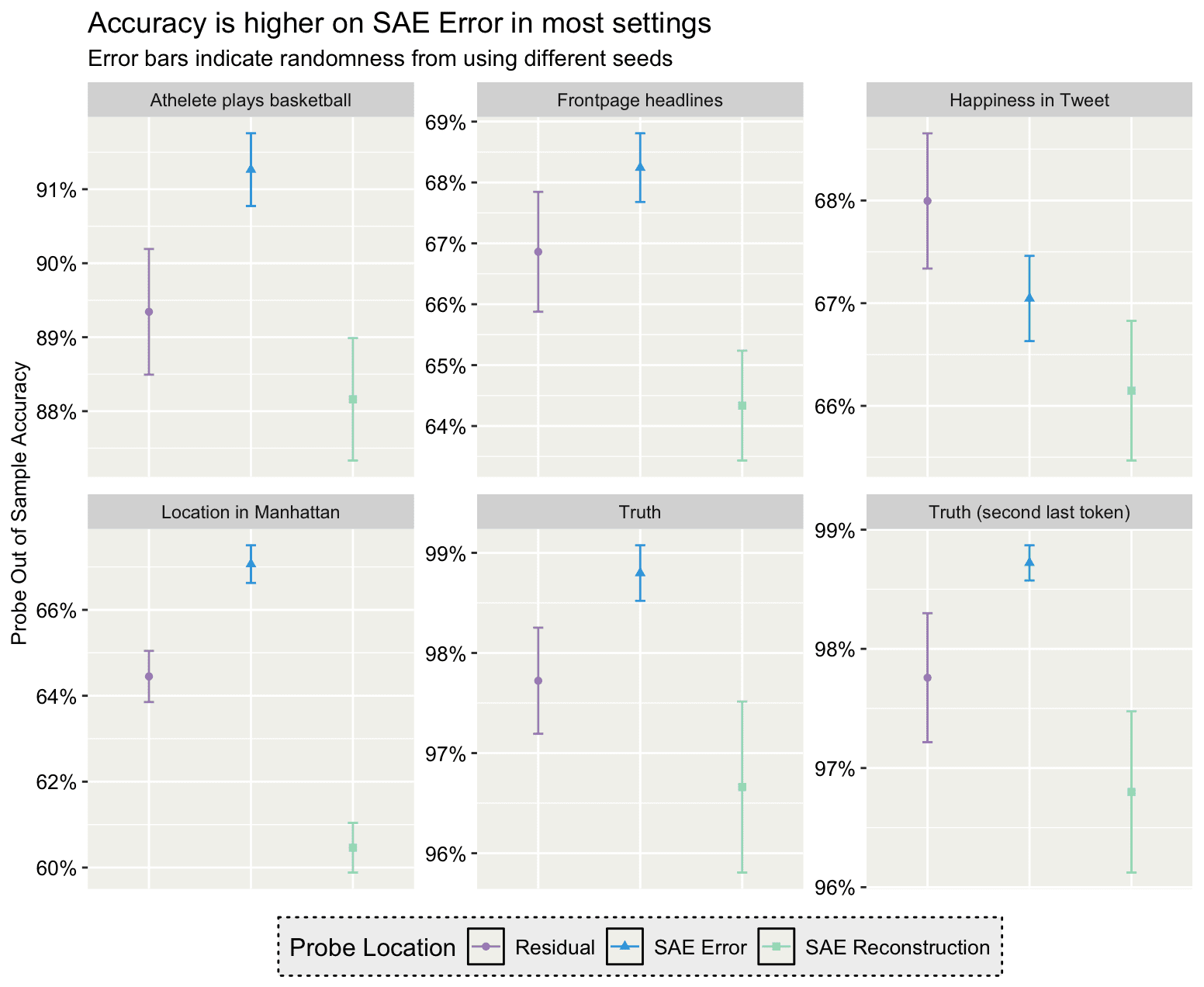
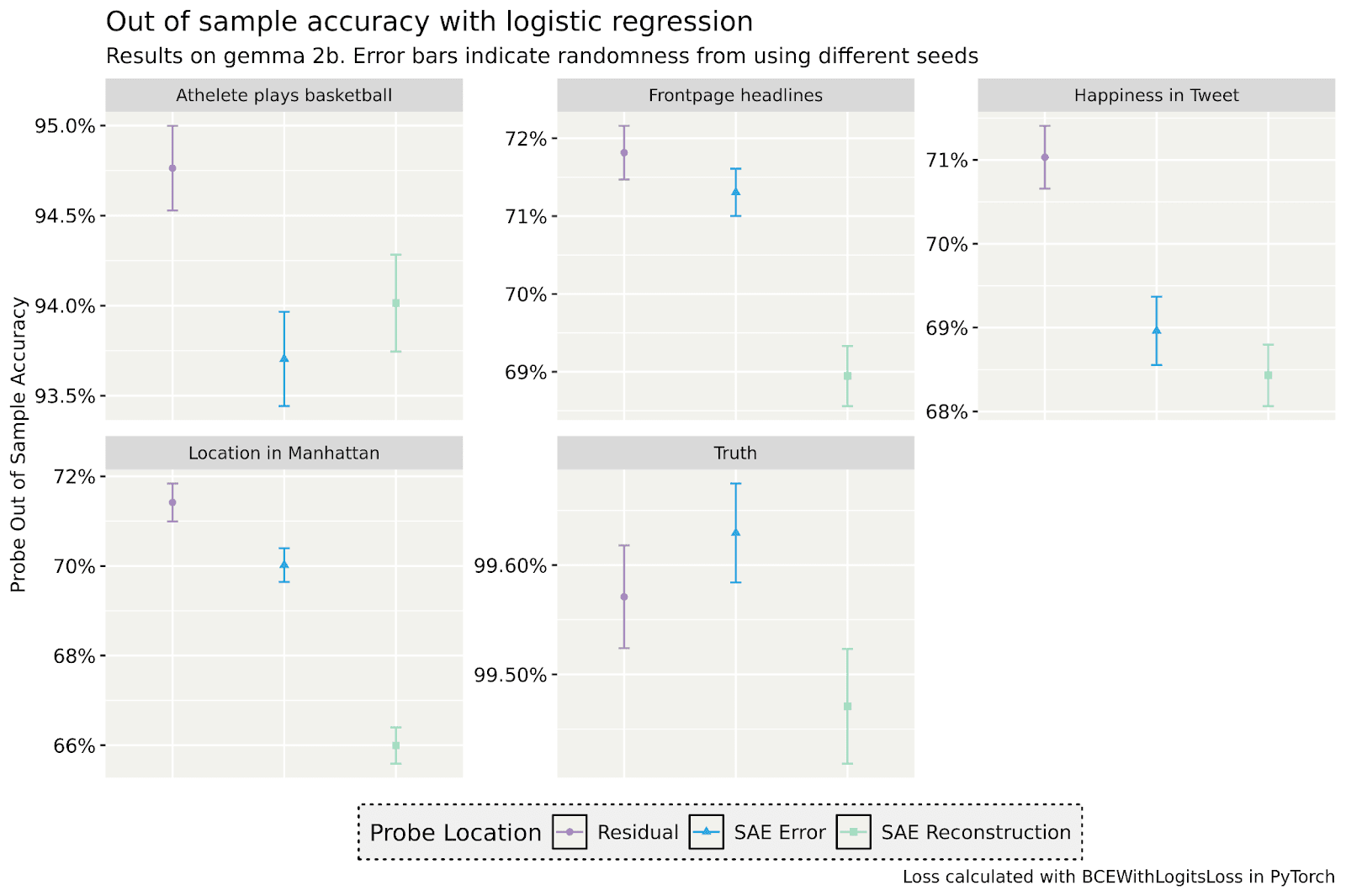
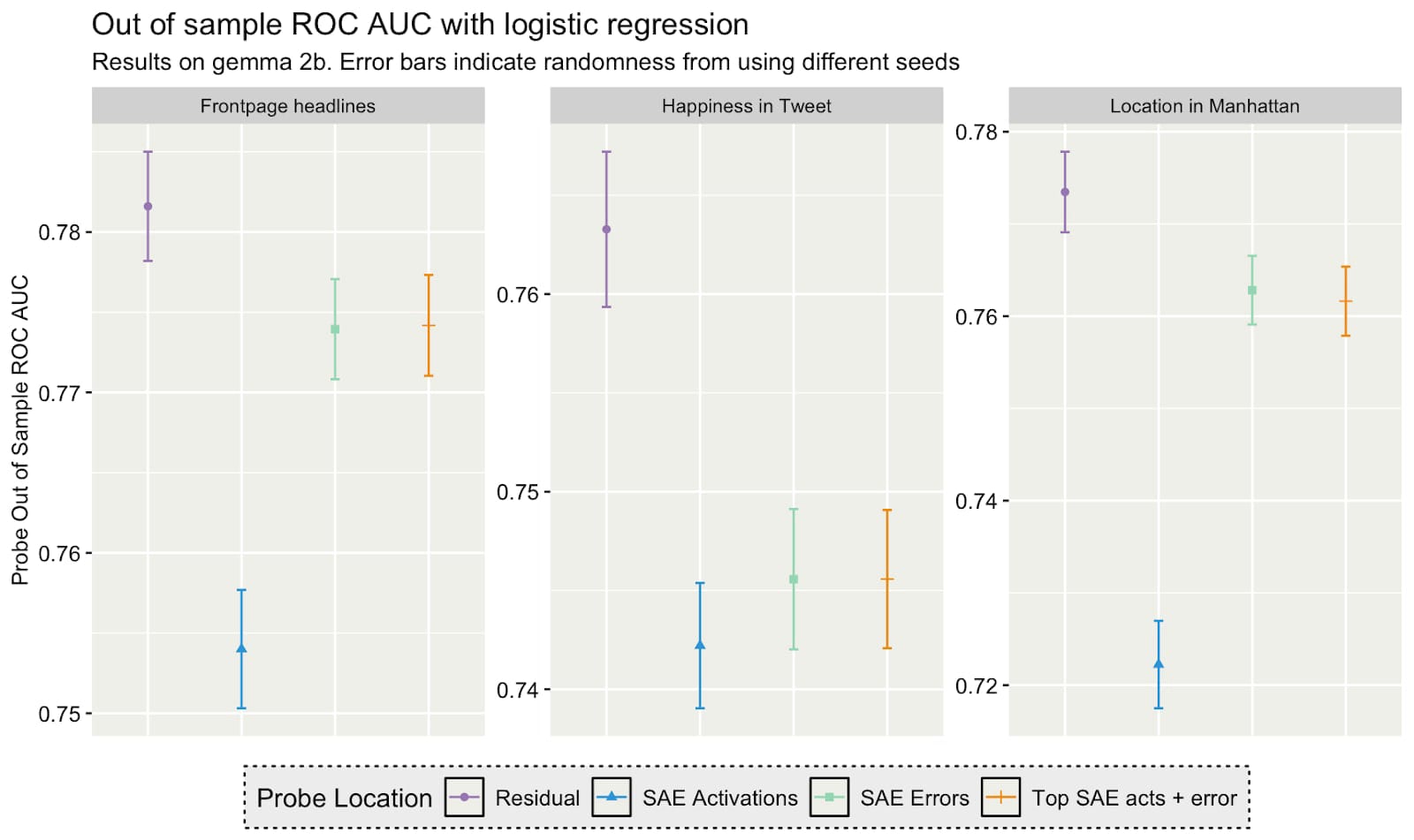
I ran some more probing experiments where I probed for arbitrary things from the datasets in from Kantamnemi et al. When using AdamW, it looks like we can get consistently more accurate probes using the SAE error.
However, if we use logistic regression to train my probes instead, I can increase my accuracy across the board, and now the SAE error no longer outperforms just probing on the residual stream. Thus, I think the previous results are likely due to the quirks of AdamW.
I also tried steering with the truth probes trained from AdamW. I took sentences of the form:
The city of Oakland is not in the United States. This statement is: False
The city of Canberra is in Australia. This statement is: True
[Some statement about cities and countries] This statement is:
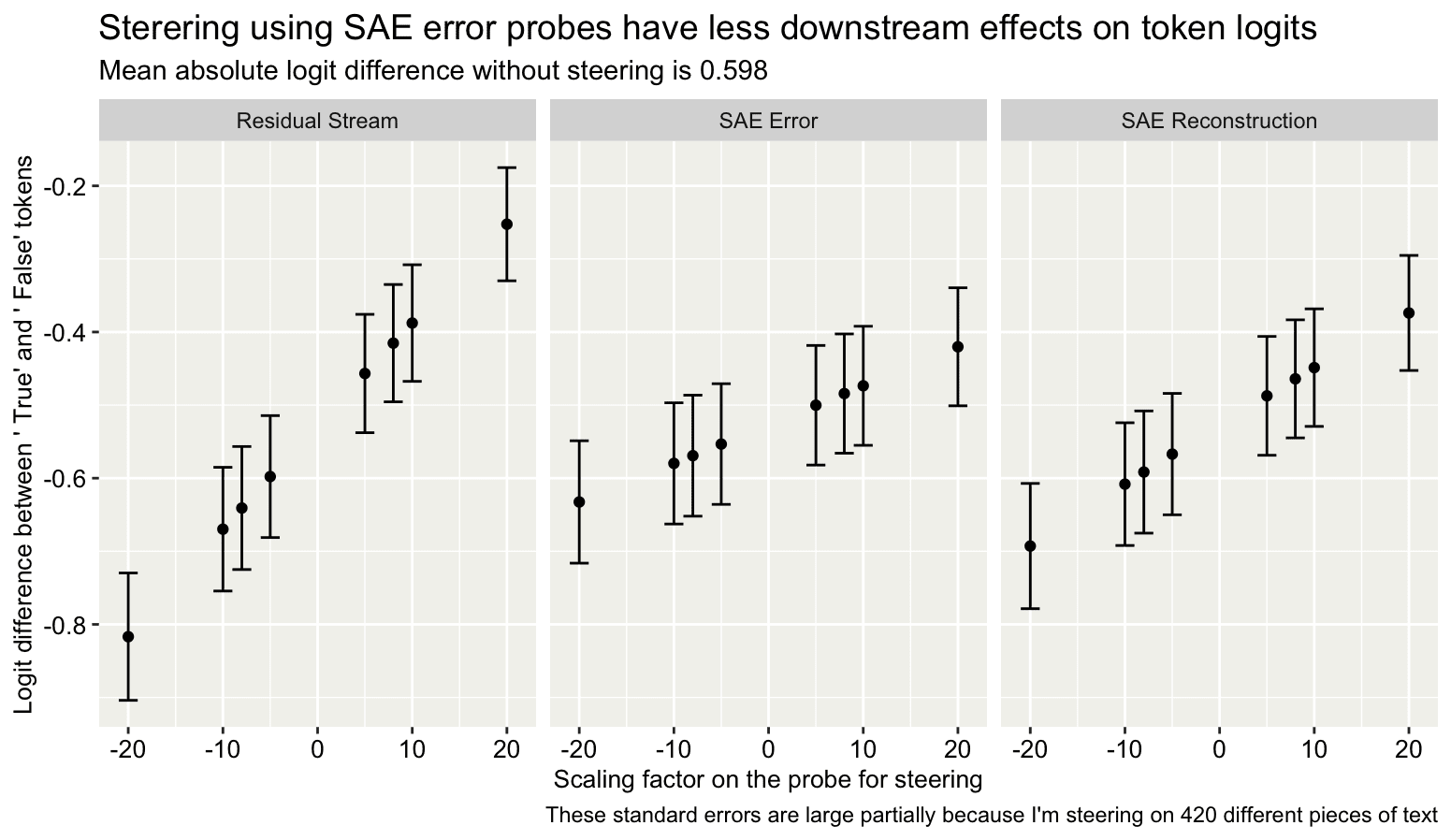
And trained new probes for truthfulness on the “:” token. I then tried to steer the next token prediction towards/away from the “ True” token. As expected, the error term probe steered less well:
Experiment three: using SAEs to remove unrelated latents
I did try one last thing: use SAEs to remove active SAE latents which are irrelevant to the concept probed before probing. In other words, I
- Train a probe on SAE hidden activations with l1 penalty
- Take the top six latents with the highest coefficient
- In a separate experiment, add the (activations in those six locations * sae.W_dec) to the error
- Train probe on the sum in (3), which represents the residual stream after it’s been de-noised.
This doesn’t really outperform probing on the residual stream either:
Author contributions statement
Taras Kutsyk: Designed and implemented the experiments in the Ablation & Restoration line of investigation; implemented the SFC replication and outlier filtering; proposed the cross-layer superposition hypothesis and developed initial strategies for testing it; conducted follow-up work with crosscoder training; wrote the corresponding sections of the post, including the introduction.
Tim Hua: Provided extensive feedback on the Ablation & Restoration results, including identifying the issue with faithfulness score outliers; envisioned the acausal crosscoder experiments and conducted the initial training runs; designed and implemented the experiments in the SAE Error Probing line of investigation; wrote the corresponding section of the post and helped edit and refine Taras’ sections.
Alice Rigg*: Provided valuable support throughout the research process; participated in regular progress check-ins and offered consistent guidance and feedback.
Andre Assis*: Served as project manager; contributed to codebase quality, facilitated regular progress check-ins, helped resolve blockers, and provided ongoing support and feedback.
*equal contribution
Acknowledgements
We thank the AISC community for providing a supportive research environment. We're especially grateful to our co-authors Alice Rigg and Andre Assis for their instrumental contributions and guidance throughout the project—even after we missed the official submission deadline.
— Taras & Tim
- ^
or at least some of them, e.g. latents that fire at least sometimes (i.e. are not “dead” in jargon) and not too frequently (e.g. less than 10% of tokens)
- ^
To make it easier/feasible to understand what’s going on, the authors group features into clusters with similar role/theme. So, the nodes of these graphs are collections of similar features rather than individual ones.
- ^
note that we don't have any model for it, it's just defined empirically as to make the equality hold.
- ^
approximations in the sense of "tight correlation" rather than "small absolute difference"
- ^
we account for the token positions because we use a templatic version of the SFC algorithm, meaning that our circuit nodes are different in different token positions. This corresponds more accurately to the transformer’s model of computation, as e.g. we have a separate residual stream for each input token position, so it’s reasonable to assume that they have different features.
- ^
SAEs capture the key computational steps which are interpretable through its features, edge attribution technique is robust etc.
- ^
We recommend checking it directly on page 24, as embedding the full figure here would compromise its quality. Instead, we’ve added custom annotations (in black) for reference.
- ^
Mathematically though, there is no contradiction: a high AtP score of this edge means that our metric experiences an approximately positive effect—up to a first-order approximation error—when we patch in the value of the “boundaries of plural NPs” upstream feature, assuming that this patching only influences the downstream error node at layer-20. So in the AtP sense of importance, layer-20 error node is important only "through the upstream NP-boundaries feature’s value, but not by itself.
- ^
by restoring the value we mean “patching from the clean forward pass” – changing the feature’s value to its original value, as it would be without any ablations.
- ^
the corresponding layer range shown in the plot is 16-21, but we rely on our previous understanding from the ablation & restoration experiment above that restoring only 16-17 layer ranges has little impact by itself.
- ^
it may be hard to follow this explanation for readers not deeply familiar with SFC, we recommend checking the Appendix A.1 of the paper where it’s explained better.
- ^
unless these error nodes are composed of quite a large number of features; then if only one of those features influences one of the downstream features, you will get a high edge weight (if both of these features are important for a circuit).
- ^
This may seem like an appeal to incredulity (“would you really believe that?”), but that’s not our intent—we’re not aiming to argue that this alternative can never be the case, but rather to explain why we lean toward the cross-layer superposition explanation.
- ^
note that any error node with non-zero AtP score must be prompt-specific to some extent, because if it had constant a value across all prompts, the AtP score would be zero by construction.