My hypothesis about what's going on here, apologies if it's already ruled out, is that we should not think of it separately computing the XOR of A and B, but rather that features A and B are computed slightly differently when the other feature is off or on. In a high dimensional space, if the vector and the vector are slightly different, then as long as this difference is systematic, this should be sufficient to successfully probe for .
For example, if A and B each rely on a sizeable number of different attention heads to pull the information over, they will have some attention heads which participate in both of them, and they would 'compete' in the softmax, where if head C is used in both writing features A and B, it will contribute less to writing feature A if it is also being used to pull across feature B, and so the representation of A will be systematically different depending on the presence of B.
It's harder to draw the exact picture for MLPs but I think similar interdependencies can occur there though I don't have an exact picture of how, interested to discuss and can try and sketch it out if people are curious. Probably would be like, neurons will participate in both, neurons which participate in A and B will be more saturated if B is active than if B is not active, so the output representation of A will be somewhat dependent on B.
More generally, I expect the computation of features to be 'good enough' but still messy and somewhat dependent on which other features are present because this kludginess allows them to pack more computation into the same number of layers than if the features were computed totally independently.
Well the substance of the claim is that when a model is calculating lots of things in superposition, these kinds of XORs arise naturally as a result of interference, so one thing to do might be to look at a small algorithmic dataset of some kind where there's a distinct set of features to learn and no reason to learn the XORs and see if you can still probe for them. It'd be interesting to see if there are some conditions under which this is/isn't true, e.g. if needing to learn more features makes the dependence between their calculation higher and the XORs more visible.
Maybe you could also go a bit more mathematical and hand-construct a set of weights which calculates a set of features in superposition so you can totally rule out any model effort being expended on calculating XORs and then see if they're still probe-able.
Another thing you could do is to zero-out or max-ent the neurons/attention heads that are important for calculating the feature, and see if you can still detect an feature. I'm less confident in this because it might be too strong and delete even a 'legitimate' feature or too weak and leave some signal in.
This kind of interference also predicts that the and features should be similar and so the degree of separation/distance from the category boundary should be small. I think you've already shown this to some extent with the PCA stuff though some quantification of the distance to boundary would be interesting. Even if the model was allocating resource to computing these XORs you'd still probably expect them to be much less salient though so not sure if this gives much evidence either way.
On xor being represented incidentally:
I find experiments where you get <<50% val acc sketchy so I quickly ran my own using a very fake dataset made out of vectors in {-1,1}^d that I pass through 10 randomly initialized ReLU MLPs with skip connections. Here, the "features" I care about are canonical directions in the input space.
What I find:
- XOR is not incidentally represented if the features are not redundant
- XOR is incidentally represented if the features are very redundant (which is often the case in Transformers, but maybe not to the extent needed for XOR to be incidentally represented). I get redundancy by using input vectors that are a concatenation of many copies of a smaller input vector.
See my code for more details: https://pastebin.com/LLjvaQLC
This is wacky but seems like a plausible thing a model might do: by doing this, the model would be able to, in later layers, make use of arbitrary boolean functions of early layer features.
This seems less wacky from a reservoir computing perspective and from the lack of recurrency: you have no idea early on what you need*, so you compute a lot of random complicated stuff up front, which is then available for the self-attention in later layers to do gradient descent on to pick out the useful features tailored to that exact prompt, and then try to execute the inferred algorithm in the time left. 'arbitrary boolean functions of early layer features' is not necessarily something I'd have expected the model to compute, but when put that way, it does seem like a bunch of those hanging around could be useful, no?
This is analogous to all the interpretability works which keep finding a theme of 'compute or retrieve everything which might be relevant up front, and then throw most of it away to do some computation with the remainder and make the final prediction'. Which is further consistent with the observations about sparsity & pruning: if most of a NN is purely speculative and exists to enable learning when one of those random functions turns out to be useful, then once learning has been accomplished, of course you can stop screwing around with speculatively computing loads of useless random things.
EDIT: if this perspective is 'the reason', I guess it would predict that at very low loss or perfect prediction, these xor features would go away unless they had a clearcut use. And that if you trained in a sparsity-creating fashion or did knowledge-distillation, then the model would also be incentivized to get rid of them. You would also maybe be able to ablate/delete them, in some way, and show that transfer learning and in-context learning become worse? I would expect any kind of recurrent or compressive approach would tend to do less of every kind of speculative computation, so maybe that would work too.
* anything in the early layers of a Transformer has no idea what is going on, because you have no recurrent state telling you anything from previous timesteps which could summarize the task or relevant state for you; and the tokens/activations are all still very local because you're still early in the forward pass. This is part of why I think the blind spot might be from early layers throwing away data prematurely, making irreversible errors.
Nice post, and glad this got settled experimentally! I think it isn't quite as counterintuitive as you make it out to be -- the observations seem like they have reasonable explanations.
I feel pretty confident that there's a systematic difference between basic features and derived features, where the basic features are more "salient" -- I'll be assuming such a distinction in the rest of the comment.
(I'm saying "derived" rather than "XOR" because it seems plausible that some XOR features are better thought of as "basic", e.g. if they were very useful for the model to compute. E.g. the original intuition for CCS is that "truth" is a basic feature, even though it is fundamentally an XOR in the contrast pair approach.)
For the more mechanistic explanations, I want to cluster them into two classes of hypotheses:
- Incidental explanations: Somehow "high-dimensional geometry" and "training dynamics" means that by default XORs of basic features end up being linearly represented as a side effect / "by accident". I think Fabien's experiments and Hoagy's hypothesis fit here.
- I think most mechanistic explanations here will end up implying a decay postulate that says "the extent to which an incidental-XOR happens decays as you have XORs amongst more and more basic features". This explains why basic features are more salient than derived features.
- Utility explanations: Actually it's often quite useful for downstream computations to be able to do logical computations on boolean variables, so during training there's a significant incentive to represent the XOR to make that happen.
- Here the reason basic features are more salient is that basic features are more useful for getting low loss, and so the model allocates more of its "resources" to those features. For example, it might use more parameter norm (penalized by weight decay) to create higher-magnitude activations for the basic features.
I think both of the issues you raise have explanations under both classes of hypotheses.
Exponentially many features:
An easy counting argument shows that the number of multi-way XORs of N features is ~. [...] There are two ways to resist this argument, which I’ll discuss in more depth later in “What’s going on?”:
- To deny that XORs of basic features are actually using excess model capacity, because they’re being represented linearly “by accident” or as an unintended consequence of some other useful computation. (By analogy, the model automatically linearly represents ANDs of arbitrary features without having to expend extra capacity.)
- To deny forms of RAX that imply multi-way XORs are linearly represented, with the model somehow knowing to compute and , but not .
While I think the first option is possible, my guess is that it's more like the second option.
On incidental explanations, this is explained by the decay postulate. For example, maybe once you hit 3-way XORs, the incidental thing is much less likely to happen, and so you get ~ pairwise XORs instead of the full ~ set of multi-way XORs.
On utility explanations, you would expect that multi-way XORs are much less useful for getting low loss than two-way XORs, and so computation for multi-way XORs is never developed.
Generalization:
logistic regression on the train set would learn the direction where is the direction representing a feature f. [...] the argument above would predict that linear probes will completely fail to generalize from train to test. This is not the result that we typically see [...]
One of these assumptions involves asserting that “basic” feature directions (those corresponding to a and b) are “more salient” than directions representing XORs – that is, the variance along and is larger than variance along . However, I’ll note that:
- it’s not obvious why something like this would be true, suggesting that we’re missing a big part of the story for why linear probes ever generalize;
- even if “basic” feature directions are more salient, the argument here still goes through to a degree, implying a qualitatively new reason to expect poor generalization from linear probes.
For the first point I'd note that (1) the decay postulate for incidental explanations seems so natural and (2) the "derived features are less useful than basic features and so have less resources allocated to them" seems sufficient for utility explanations.
For the second point, I'm not sure that the argument does go through. In particular you now have two possible outs:
- Maybe if is twice as salient as , you learn a linear probe that is entirely , or close enough to it (e.g. if it is exponentially closer). I'd guess this isn't the explanation, but I don't actually know what linear probe learning theory predicts here.
- Even if you do learn , it doesn't seem obvious that test accuracy should be < 100%. In particular, if is more salient by having activations that are twice as large, then it could be that even when b flips from 0 to 1 and is reversed, still overwhelms and so every input is still classified correctly (with slightly less confidence than before).
On the other hand, RAX introduces a qualitatively new way that linear probes can fail to learn good directions. Suppose a is a feature you care about (e.g. “true vs. false statements”) and b is some unrelated feature which is constant in your training data (e.g. b = “relates to geography”). [...]
This is wild. It implies that you can’t find a good direction for your feature unless your training data is diverse with respect to every feature that your LLM linearly represents.
Fwiw, failures like this seem plausible without RAX as well. We explicitly make this argument in our goal misgeneralization paper (bottom of page 9 / Section 4.2), and many of our examples follow this pattern (e.g. in Monster Gridworld, you see a distribution shift from "there is almost always a monster present" in training to "there are no monsters present" at test time).
I agree strong RAX without any saliency differences between features would imply this problem is way more widespread than it seems to be in practice, but I don't think it's a qualitatively new kind of generalization failure (and also I think strong RAX without saliency differences is clearly false).
Maybe models track which features are basic and enforce that these features be more salient
In other words, maybe the LLM is recording somewhere the information that a and b are basic features; then when it goes to compute , it artificially makes this direction less salient. And when the model computes a new basic feature as a boolean function of other features, it somehow notes that this new feature should be treated as basic and artificially increases the salience along the new feature direction.
I don't think the model has to do any active tracking; on both hypotheses this happens by default (in incidental explanations, because of the decay postulate, and in utility explanations, because the feature is less useful and so fewer resources go towards computing it).
I agree with a lot of this, but some notes:
Exponentially many features
[...]
On utility explanations, you would expect that multi-way XORs are much less useful for getting low loss than two-way XORs, and so computation for multi-way XORs is never developed.
The thing that's confusing here is that the two-way XORs that my experiments are looking at just seem clearly not useful for anything. So I think any utility explanation that's going to be correct needs to be a somewhat subtle one of the form "the model doesn't initially know which XORs will be useful, so it just dumbly computes way more XORs than it needs, including XORs which are never used in any example in training." Or in other words "the model has learned the algorithm 'compute lots of XORs' rather than having learned specific XORs which it's useful to compute."
I think this subtlety changes the story a bit. One way that it changes the story is that you can't just say "the model won't compute multi-way XORs because they're not useful" -- the two-way XORs were already not useful! You instead need to argue that the model is implementing an algorithm which computed all the two-way XORs but didn't compute XORs of XORs; it seems like this algorithm might need to encode somewhere information about which directions correspond to basic features and which don't.
On the other hand, RAX introduces a qualitatively new way that linear probes can fail to learn good directions. Suppose a is a feature you care about (e.g. “true vs. false statements”) and b is some unrelated feature which is constant in your training data (e.g. b = “relates to geography”). [...]
Fwiw, failures like this seem plausible without RAX as well. We explicitly make this argument in our goal misgeneralization paper (bottom of page 9 / Section 4.2), and many of our examples follow this pattern (e.g. in Monster Gridworld, you see a distribution shift from "there is almost always a monster present" in training to "there are no monsters present" at test time).
Even though on a surface level this resembles the failure discussed in the post (because one feature is held fixed during training), I strongly expect that the sorts of failures you cite here are really generalization failure for "the usual reasons" of spurious correlations during training. For example, during training (because monsters are present), "get a high score" and "pick up shields" are correlated, so the agents learn to value picking up shields. I predict that if you modified the train set so that it's no longer useful to pick up shields (but monsters are still present), then the agent would no longer pick up shields, and so would no longer misgeneralize in this particular way.
In contrast, the point I'm trying to make in the post is that RAX can cause problems even in the absence of spurious correlations like this.[1]
I don't think the model has to do any active tracking; on both hypotheses this happens by default (in incidental explanations, because of the decay postulate, and in utility explanations, because the feature is less useful and so fewer resources go towards computing it).
As you noted, it will sometimes be the case that XOR features are more like basic features than derived features, and thus will be represented with high salience. I think incidental hypotheses will have a really hard time explaining this -- do you agree?
For utility hypotheses, the point is that there needs to be something different in model internals which says "when computing these features represent the result with low salience, but when computing these features represent the result with high salience." Maybe on your model this is something simple like the weights computing the basic features being larger than weights computing derived features? If so, that's the tracking I'm talking about, and is a potential thread to pull on for distinguishing basic vs. derived features using model internals.
- ^
If you want you could rephrase this issue as " and are spuriously correlated in training," so I guess I should say "even in the absence of spurious correlations among basic features."
The thing that's confusing here is that the two-way XORs that my experiments are looking at just seem clearly not useful for anything.
Idk, I think it's pretty hard to know what things are and aren't useful for predicting the next token. For example, some of your features involve XORing with a "has_not" feature -- XORing with an indicator for "not" might be exactly what you want to do to capture the effect of the "not".
(Tbc here the hypothesis could be "the model computes XORs with has_not all the time, and then uses only some of them", so it does have some aspect of "compute lots of XORs", but it is still a hypothesis that clearly by default doesn't produce multiway XORs.)
In contrast, the point I'm trying to make in the post is that RAX can cause problems even in the absence of spurious correlations like this.[1]
If you want you could rephrase this issue as " and are spuriously correlated in training," so I guess I should say "even in the absence of spurious correlations among basic features."
... That's exactly how I would rephrase the issue and I'm not clear on why you're making a sharp distinction here.
As you noted, it will sometimes be the case that XOR features are more like basic features than derived features, and thus will be represented with high salience. I think incidental hypotheses will have a really hard time explaining this -- do you agree?
I mean, I'd say the ones that are more like basic features are like that because it was useful, and it's all the other XORs that are explained by incidental hypotheses. The incidental hypotheses shouldn't be taken to be saying that all XORs are incidental, just the ones which aren't explained by utility. Perhaps a different way of putting it is that I expect both utility and incidental hypotheses to be true to some extent.
Maybe on your model this is something simple like the weights computing the basic features being larger than weights computing derived features? If so, that's the tracking I'm talking about, and is a potential thread to pull on for distinguishing basic vs. derived features using model internals.
Yes, on my model it could be something like the weights for basic features being large. It's not necessarily that simple, e.g. it could also be that the derived features are in superposition with a larger number of other features that leads to more interference. If you're calling that "tracking", fair enough I guess; my main claim is that it shouldn't be surprising. I agree it's a potential thread for distinguishing such features.
Idk, I think it's pretty hard to know what things are and aren't useful for predicting the next token. For example, some of your features involve XORing with a "has_not" feature -- XORing with an indicator for "not" might be exactly what you want to do to capture the effect of the "not".
I agree that "the model has learned the algorithm 'always compute XORs with has_not'" is a pretty sensible hypothesis. (And might be useful to know, if true!) FWIW, the stronger example of "clearly not useful XORs" I was thinking of has_true XOR has_banana, where I'm guessing you're anticipating that this XOR exists incidentally.
If you want you could rephrase this issue as " and are spuriously correlated in training," so I guess I should say "even in the absence of spurious correlations among basic features."
... That's exactly how I would rephrase the issue and I'm not clear on why you're making a sharp distinction here.
Focusing again on the Monster gridworld setting, here are two different ways that your goals could misgeneralize:
- player_has_shield is spuriously correlated with high_score during training, so the agent comes to value both
- monster_present XOR high_score is spuriously correlated with high_score during training, so the agent comes to value both.
These are pretty different things that could go wrong. Before realizing that these crazy XOR features existed, I would only have worried about (1); now that I know these crazy XOR features exist ... I think I mostly don't need to worry about (2), but I'm not certain and it might come down to details about the setting. (Indeed, your CCS challenges work has shown that sometimes these crazy XOR features really can get in the way!)
I agree that you can think of this issue as just being the consequence of the two issues "there are lots of crazy XOR features" and "linear probes can pick up on spurious correlations," I guess this issue feels qualitatively new to me because it just seems pretty untractable to deal with it on the data augmentation level (how do you control for spurious correlations with arbitrary boolean functions of undesired features?). I think you mostly need to hope that it doesn't matter (because the crazy XOR directions aren't too salient) or come up with some new idea.
I'll note that if it ends up these XOR directions don't matter for generalization in practice, then I start to feel better about CCS (along with other linear probing techniques).[1]
my main claim is that it shouldn't be surprising
If I had to articulate my reason for being surprised here, it'd be something like:
- I didn't expect LLMs to compute many XORs incidentally
- I didn't expect LLMs to compute many XORs because they are useful
but lots of XORs seem to get computed anyway. So at least one of these two mechanisms is occurring a surprising (to me) amount. If there's a lot more incidental computation, then why? (Based on Fabian's experiments, maybe the answer is "there's more redundancy than I expected," which would be interesting.) If there's a lot more intentional computation of XORs than I expected, then why? (I've found the speculation that LLMs might just computing a bunch of XORs up front because they don't know what they'll need later interesting.) I could just update my world model to "lots of XORs exist for either reasons (1) or (2)," but I sure would be interested in knowing which of (1) or (2) it is and why.
- ^
I know that for CCS you're more worried about issues around correlations with features like true_according_to_Alice, but my feeling is that we might be able to handle spurious features that are that crazy and numerous, but not spurious features as crazy and numerous as these XORs.
I think you mostly need to hope that it doesn't matter (because the crazy XOR directions aren't too salient) or come up with some new idea.
Yeah certainly I'd expect the crazy XOR directions aren't too salient.
I'll note that if it ends up these XOR directions don't matter for generalization in practice, then I start to feel better about CCS (along with other linear probing techniques). I know that for CCS you're more worried about issues around correlations with features like true_according_to_Alice, but my feeling is that we might be able to handle spurious features that are that crazy and numerous, but not spurious features as crazy and numerous as these XORs.
Imo "true according to Alice" is nowhere near as "crazy" a feature as "has_true XOR has_banana". It seems useful for the LLM to model what is true according to Alice! (Possibly I'm misunderstanding what you mean by "crazy" here.)
I'm not against linear probing techniques in general. I like linear probes, they seem like a very useful tool. I also like contrast pairs. But I would basically always use these techniques in a supervised way, because I don't see a great reason to expect unsupervised methods to work better.
If I had to articulate my reason for being surprised here, it'd be something like:
- I didn't expect LLMs to compute many XORs incidentally
- I didn't expect LLMs to compute many XORs because they are useful
but lots of XORs seem to get computed anyway.
This is reasonable. My disagreement is mostly that I think LLMs are complicated things and do lots of incidental stuff we don't yet understand. So I shouldn't feel too surprised by any given observation that could be explained by an incidental hypothesis. But idk it doesn't seem like an important point.
Imo "true according to Alice" is nowhere near as "crazy" a feature as "has_true XOR has_banana". It seems useful for the LLM to model what is true according to Alice! (Possibly I'm misunderstanding what you mean by "crazy" here.)
I agree with this! (And it's what I was trying to say; sorry if I was unclear.) My point is that
{ features which are as crazy as "true according to Alice" (i.e., not too crazy)}
seems potentially manageable, where as
{ features which are as crazy as arbitrary boolean functions of other features }
seems totally unmanageable.
Thanks, as always, for the thoughtful replies.
I reran my experiments from above on a “reset” version of LLaMA-2-13B. What this means is that, for each parameter in LLaMA-2-13B, I shuffled the weights of that parameter by permuting them along the last dimension
Why do you get <50% accuracy for any of the categories? Shouldn't a probe trained on any reasonable loss function always get >50% accuracy on any binary classification task?
I'm not really sure, but I don't think this is that surprising. I think when we try to fit a probe to "label" (the truth value of the statement), this is probably like fitting a linear probe to random data. It might overfit on some token-level heuristic which is ideosyncratically good on the train set but generalizes poorly to the val set. E.g. if disproportionately many statements containing "India" are true on the train set, then it might learn to label statements containing "India" as true; but since in the full dataset, there is no correlation between "India" and being true, correlation between "India" and true in the val set will necessarily have the opposite sign.
Are the training and val sets not IID? Are they small enough that we either get serious overfit or huge error bars?
If the datasets are IID and large and the loss function is reasonable, then if there is just noise, the probe should learn to just always predict the more common class and not have any variance. This should always result in >50% accuracy.
There's 1500 statements in each of cities and neg_cities, and LLaMA-2-13B has residual stream dimension 5120. The linear probes are trained with vanilla logistic regression on {80% of the data in cities} \cup {80% of the data in neg_cities} and the accuracies reported are evaluated on {remaining 20% of the data in cities} \cup {remaining 20% of the data in neg_cities}.
So, yeah, I guess that the train and val sets are drawn from the same distribution but are not independent (because of the issue I mentioned in my comment above). Oops! I guess I never thought about how with small datasets, doing an 80/20 train/test split can actually introduce dependencies between the train and test data. (Also yikes, I see people do this all the time.)
Anyway, it seems to me that this is enough to explain the <50% accuracies -- do you agree?
Using a dataset of 10,000 inputs of the form[random LLaMA-13B generated text at temperature 0.8] [either the most likely next token or the 100th most likely next token, according to LLaMA-13B] ["true" or "false"] ["banana" or "shed"]
I've rerun the probing experiments. The possible labels are
- has_true: is the second last token "true" or "false"?
- has_banana: is the last token "banana" or "shed"?
- label: is the third last token the most likely or the 100th most likely?
(this weird last option is because I'm adapting a dataset from the Geometry of Truth paper about likely vs. unlikely text).
Here are the results for LLaMA-2-13B

And here are the results for the reset network
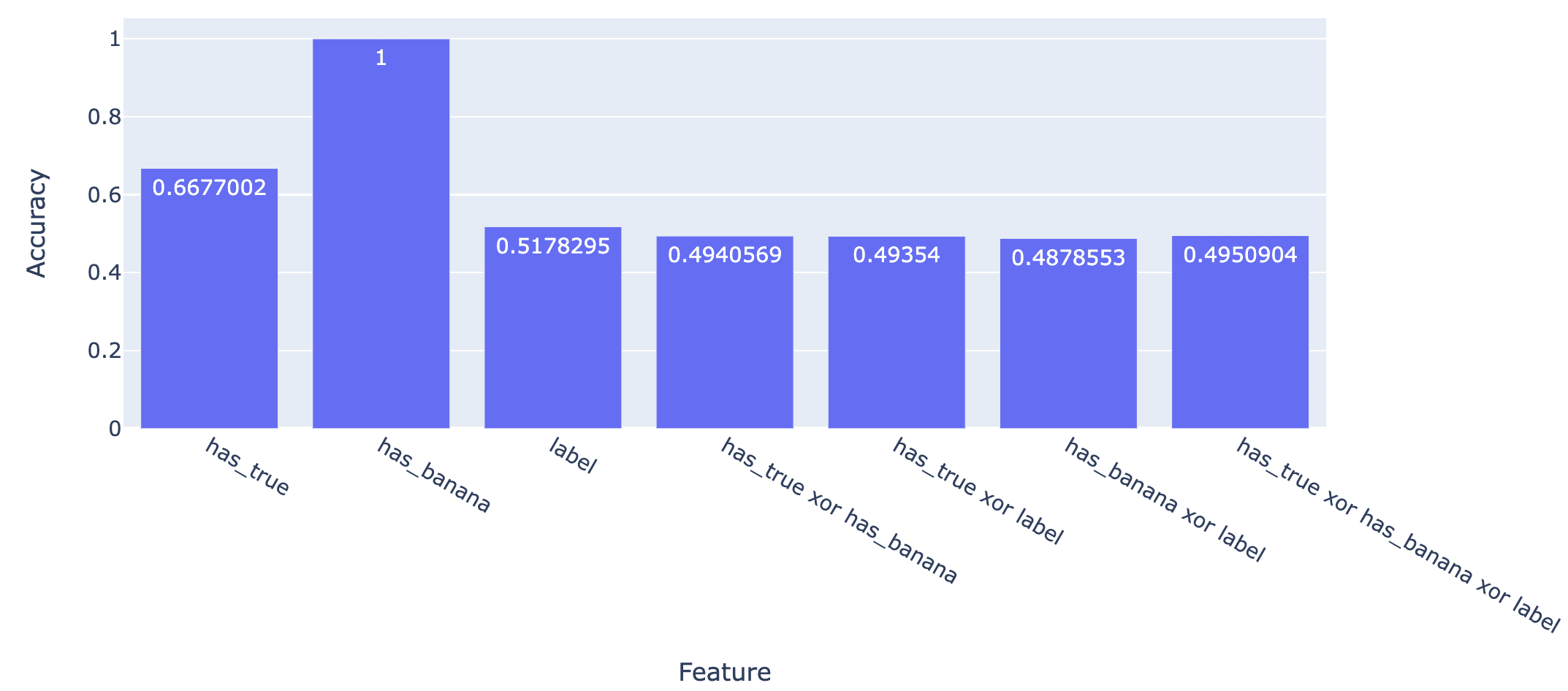
I was a bit surprised that the model did so badly on has_true, but in hindsight, considering that the activations are extracted over the last token and "true"/"false" is the penultimate token, this seems fine.
Mostly I view this as a sanity check to make sure that when the dataset is larger we don't get the <<50% probe accuracies. I think to really dig into this more, one would need to do this with features which are not token-level and which are unambiguously linearly accessible (unlike the "label" feature here).
Yep I think I agree, I didn't understand the point you made about systematic anti-correlation originally.
If I understand correctly the issues is something like:
- There are 10 India related statements, exactly 5 of which are false and 5 of which are true.
- We do a random split of all the data, so if there is more true+india in train there will be more false+india in test
There are of course various fixes to make the data actually IID.
Prediction: token level features or other extremely salient features are XOR'd with more things than less salient features. And if you find less salient things which are linearly represented, a bunch of this won't be XOR'd.
This solves the exponential blow up and should also make sense with your experimental results (where all of the features under consideration are probably in the top 50 or so for salience).
(Are you saying that you think factuality is one of the 50 most salient features when the model processes inputs like "The city of Chicago is not in Madagascar."? I think I'd be pretty surprised by this.)
(To be clear, factuality is one of the most salient feature relative to the cities/neg_cities datasets, but it seems like the right notion of salience here is relative to the full data distribution.)
Yes, that's what I'm saying. I think this is right? Note that we only need salience on one side between false and true, so "true vs false" is salient as long as "false" is salient. I would guess that "this is false" is very salient for this type of data even for a normal pretrained LLM.
(Similarly, "this is english" isn't salient in a dataset of only english, but is salient in a dataset with both english and spanish: salience depends on variation. Really, the salient thing here is "this is spanish" or "this is false" and then the model will maybe XOR these with the other salient features. I think just doing the XOR on one "side" is sufficient for always being able to compute the XOR, but maybe I'm confused or thinking about this wrong.)
Idk, I think I would guess that all of the most salient features will be things related to the meaning of the statement at a more basic level. E.g. things like: the statement is finished (i.e. isn't an ongoing sentence), the statement is in English, the statement ends in a word which is the name of a country, etc.
My intuition here is mostly based on looking at lots of max activating dataset examples for SAE features for smaller models (many of which relate to basic semantic categories for words or to basic syntax), so it could be bad here (both because of model size and because the period token might carry more meta-level "summarized" information about the preceding statement).
Anyway, not really a crux, I would agree with you for some not-too-much-larger value of 50.
I'm having some trouble replicating this result in a not exactly comparable setting (internal model, looking at is_alice xor amazon_sentiment). I get 90%+ on the constituent datasets, but only up to 75% on the xor depending on which layer I look at.
(low confidence, will update as I get more results)
The training set is a random 100k subsample of this dataset: https://huggingface.co/datasets/amazon_polarity
I'm prepending Alice/Bob and doing the xor of the label in exactly the same way you do.
Take this set contains exponentially many points. Is there Any function such that all exponentially many xor combos can be found by a linear probe?
This is a question of pure maths, it involves no neural networks. And I think it would be highly informative.
Suppose has a natural interpretation as a feature that the model would want to track and do downstream computation with, e.g. if a = “first name is Michael” and b = “last name is Jordan” then can be naturally interpreted as “is Michael Jordan”. In this case, it wouldn’t be surprising the model computed this AND as and stored the result along some direction independent of and . Assuming the model has done this, we could then linearly extract with the probe
for some appropriate and .[7]
Should the be inside the inner parentheses, like for ?
In the original equation, if AND are both present in , the vectors , , and would all contribute to a positive inner product with , assuming . However, for XOR we want the and inner products to be opposing the inner product such that we can flip the sign inside the sigmoid in the AND case, right?
Here's a fun thing I noticed:
There are 16 boolean functions of two variables. Now consider an embedding that maps each of the four pairs {(A=true, B=true), (A=true, B=false), ...} to a point in 2d space. For any such embedding, at most 14 of the 16 functions will be representable with a linear decision boundary.
For the "default" embedding (x=A, y=B), xor and its complement are the two excluded functions. If we rearrange the points such that xor is linearly represented, we always lose some other function (and its complement). In fact, there are 7 meaningfully distinct colinearity-free embeddings, each of which excludes a different pair of functions.[1]
I wonder how this situation scales for higher dimensions and variable counts. It would also make sense to consider sparse features (which allow superposition to get good average performance).
- ^
The one unexcludable pair is ("always true", "always false").
These are the seven embeddings:
Maybe models track which features are basic and enforce that these features be more salient
Couldn't it just write derivative features more weakly, and therefore not need any tracking mechanism other than the magnitude itself?
Some features which are computed from other features should probably themselves be treated as basic and thus represented with large salience.
If anyone would like to replicate these results, the code can be found in the rax branch of my geometry-of-truth repo. This was adapted from a codebase I used on a different project, so there's a lot of uneeded stuff in this repo. The important parts here are:
- The datasets: cities_alice.csv and neg_cities_alice.csv (for the main experiments I describe), cities_distractor.csv and neg_cities_distractor.csv (for the experiments with banana/shed at the end of factual statements), and xor.csv (for the experiments with true/false and banana/shed after random text).
- xor_probing.ipynb: my code for doing the probing and making the plots. This assumes that the activations have already been extracted and saved using generate_acts.py (see the readme for info about how to use generate_acts.py).
Unless you want to do PCA visualizations, I'd probably recommend just taking my datasets and quickly writing your own code to do the probing experiments, rather than spending time trying to figure out my infrastructure here.
I’ll say that a model linearly represents a binary feature f if there is a linear probe out of the model’s latent space which is accurate for classifying f
If a model linearly represents features a and b, then it automatically linearly represents and .
I think I misunderstand your definition. Let feature a be represented by x_1 > 0.5, and let feature b be represented by x_2 > 0.5. Let x_i be iid uniform [0, 1]. Isn't that a counterexample to (a and b) being linearly representable?
Thanks, you're correct that my definition breaks in this case. I will say that this situation is a bit pathological for two reasons:
- The mode of a uniform distribution doesn't coincide with its mean.
- The variance of the multivariate uniform distribution is largest along the direction , which is exactly the direction which we would want to represent a AND b.
I'm not sure exactly which assumptions should be imposed to avoid pathologies like this, but maybe something of the form: we are working with boolean features whose class-conditional distributions satisfy properties like
- are unimodal, and their modes coincide with their means
- The variance of along any direction is not too large relative to the difference of the means
The variance of the multivariate uniform distribution is largest along the direction , which is exactly the direction which we would want to represent a AND b.
The variance is actually the same in all directions. One can sanity-check by integration that the variance is 1/12 both along the axis and along the diagonal.
In fact, there's nothing special about the uniform distribution here: The variance should be independent of direction for any N-dimensional joint distribution where the N constituent distributions are independent and have equal variance.[1]
The diagram in the post showing that "and" is linearly represented works if the features are represented discretely (so that there are exactly 4 points for 2 binary features, instead of a distribution for each combination). As soon as you start defining features with thresholds like DanielVarga did, the argument stops going through in general, and the claim can become false.
The stuff about unimodality doesn't seem relevant to me, and in fact seems directionally wrong.
- ^
I have a not-fully-verbalized proof which I don't have time to write out
Thanks, you're totally right about the equal variance thing -- I had stupidly thought that the projection of onto y = x would be uniform on (obviously false!).
The case of a fully discrete distribution (supported in this case on four points) seems like a very special case of a something more general, where a "more typical" special case would be something like:
- if a, b are both false, then sample from
- if a is true and b is false, then sample from
- if a is false and b is true then sample from
- if a and b are true, then sample from
for some and covariance matrix . In general, I don't really expect the class-conditional distributions to be Gaussian, nor for the class-conditional covariances to be independent of the class. But I do expect something broadly like this, where the distributions are concentrated around their class-conditional means with probability falling off as you move further from the class-conditional mean (hence unimodality), and that the class-conditional variances are not too big relative to the distance between the clusters.
Given that longer explanation, does the unimodality thing still seem directionally wrong?
Oops, I misunderstood what you meant by unimodality earlier. Your comment seems broadly correct now (except for the variance thing). I would still guess that unimodality isn't precisely the right well-behavedness desideratum, but I retract the "directionally wrong".
I think that linearly available XOR would occur if the model makes linearly available any boolean function which is "linearly independent" from the two values individually. So, maybe this could be implemented via something other than XOR, which is maybe more natural?
What is "this"? It sounds like you're gesturing at the same thing I discuss in the section "Maybe is represented “incidentally” because it’s possible to aggregate noisy signals from many features which are correlated with boolean functions of a and b"
The thing that remains confusing here is that for arbitrary features like these, it's not obvious why the model is computing any nontrivial boolean function of them and storing it along a different direction. And if the answer is "the model computes this boolean function of arbitrary features" then the downstream consequences are the same, I think.
I edited my comment. I'm just trying to say that like how you get for free, you also get XOR for free if you compute anything else which is "linearly independent" frrom the components a and b. (For a slightly fuzzy notion of linear independence where we just need separability.)
Wild.
The difference in variability doesn't seem like it's enough to explain the generalization, if your PC-axed plots are on the same scale. But maybe that's misleading because the datapoints are still kinda muddled in the has_alice xor has_not plot, and separating them might require going to more dimensions, that have smaller variability.
Thanks to Clément Dumas, Nikola Jurković, Nora Belrose, Arthur Conmy, and Oam Patel for feedback.
In the comments of the post on Google Deepmind’s CCS challenges paper, I expressed skepticism that some of the experimental results seemed possible. When addressing my concerns, Rohin Shah made some claims along the lines of “If an LLM linearly represents features a and b, then it will also linearly represent their XOR, a⊕b, and this is true even in settings where there’s no obvious reason the model would need to make use of the feature a⊕b.”[1]
For reasons that I’ll explain below, I thought this claim was absolutely bonkers, both in general and in the specific setting that the GDM paper was working in. So I ran some experiments to prove Rohin wrong.
The result: Rohin was right and I was wrong. LLMs seem to compute and linearly represent XORs of features even when there’s no obvious reason to do so.
I think this is deeply weird and surprising. If something like this holds generally, I think this has importance far beyond the original question of “Is CCS useful?”
In the rest of this post I’ll:
Overall, this has left me very confused: I’ve found myself simultaneously having (a) an argument that A⟹B, (b) empirical evidence of A, and (c) empirical evidence of ¬B. (Here A = RAX and B = other facts about LLM representations.)
The RAX claim: LLMs linearly represent XORs of arbitrary features, even when there’s no reason to do so
To keep things simple, throughout this post, I’ll say that a model linearly represents a binary feature f if there is a linear probe out of the model’s latent space which is accurate for classifying f; in this case, I’ll denote the corresponding direction as vf. This is not how I would typically use the terminology “linearly represents” – normally I would reserve the term for a stronger notion which, at minimum, requires the model to actually make use of the feature direction when performing cognition involving the feature[2]. But I’ll intentionally abuse the terminology here because I don’t think this distinction matters much for what I’ll discuss.
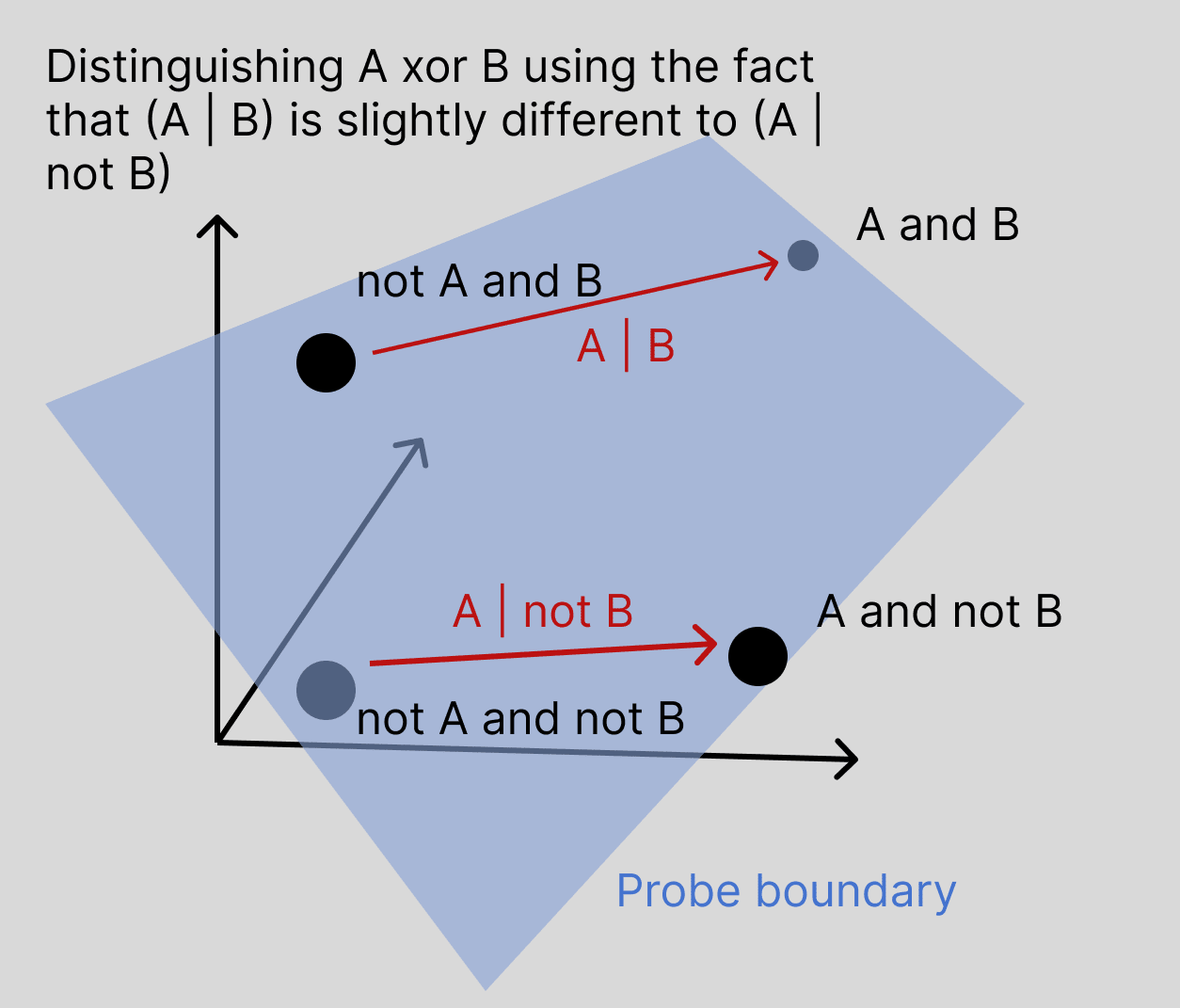
If a model linearly represents features a and b, then it automatically linearly represents a∧b and a∨b.
However, a⊕b is not automatically linearly represented – no linear probe in the figure above would be accurate for classifying a⊕b. Thus, if the model wants to make use of the feature a⊕b, then it needs to do something additional: allocate another direction[3] (more model capacity) to representing a⊕b, and also perform the computation of a⊕b so that it knows what value to store along this new direction.
The representation of arbitrary XORs (RAX) claim, in its strongest form, asserts that whenever a LLM linearly represents features a and b, it will also linearly represent a⊕b. Concretely, this might look something like: in layer 5, the model computes and linearly represents the features “has positive sentiment” and “relates to soccer”, and then in layer 6 the model computes and represents “has positive sentiment” XOR “relates to soccer”.
Why might models represent XORs? In the CCS challenges post’s comment thread, Rohin offered one explanation: if a, b, and a⊕b are linearly represented, then any boolean function of a and b is also linearly represented. On the other hand, as I’ll argue in the next section, this comes at the cost of exponentially increasing the amount of capacity the model needs to allocate.
RAX would be very surprising
In this section I’ll go through some implications of RAX. First I’ll argue that RAX implies linear probes should never generalize at all across even very minor distributional shifts. Second, I’ll argue that if you previously thought LLMs linearly represent N features, RAX would imply that LLMs actually linearly represent exp(N) features (including XORs of features). These arguments aren’t proofs, and in “What’s going on?”, I’ll discuss some additional assumptions one could make about the structure of model internals that would make these arguments fail.
Without additional assumptions, RAX implies linear probes shouldn’t generalize
First I’ll make an overly simplistic and incorrect version of this argument as an intuition pump; then I’ll explain the correct version of this argument.
Suppose there are two features, a and b, and we train a linear probe to classify a on a dataset where b is always false. What will the accuracy of this probe be when evaluated on a test dataset where b is always true?
<incorrect argument>
Assuming RAX, there are two features which get high accuracy on the training data: a and a⊕b. The former feature gets 100% accuracy on the test data, and the latter feature gets 0%, so on average we should expect 50% accuracy.
</incorrect argument>
The issue with the above argument is that the direction learned by the probe won’t align with either the a direction or the a⊕b direction, but will be a linear combination of the two. So here’s how to make the above argument properly: let’s assume that the directions representing a, b, and a⊕b are orthogonal and the variation along these directions is equal (i.e. all of the features are “equally salient”). Then as shown by the figure below, logistic regression on the train set would learn the direction va+va⊕b where vf is the direction representing a feature f. But this direction gets 50% accuracy on the test set.
LLMs linearly represent more than two features, and there will often be many differences between the train set and the test set, but this doesn’t change the basic story: as long as there is any feature which systematically differs between the train and test set (e.g. the train set is sentiment classification for movie reviews and the test set is sentiment classification for product reviews), the argument above would predict that linear probes will completely fail to generalize from train to test.
This is not the result that we typically see: rather, there’s often (not always) considerable generalization from train to test, with generalization getting continuously worse the larger the degree of distributional shift.
In “What’s going on?”, we’ll explore additional assumptions we could enforce which would prevent this argument from going through while still being consistent with RAX. One of these assumptions involves asserting that “basic” feature directions (those corresponding to a and b) are “more salient” than directions representing XORs – that is, the variance along va and vb is larger than variance along va⊕b. However, I’ll note that:
I’ll discuss these issues more in “What RAX means for people who work with model internals”.
Models have exponentially more stuff than you thought they did
Let’s say you previously thought that your model was keeping track of three features: a, b, and c. If RAX is true, then it implies that your model is also keeping track not only of a⊕b, a⊕c, and b⊕c, but also a⊕b⊕c (since it is the XOR of a and b⊕c). An easy counting argument shows that the number of multi-way XORs of N features is ~2N. I think that for most people, learning that models have exponentially more stuff than they previously thought should be a massive, surprising update.
There are two ways to resist this argument, which I’ll discuss in more depth later in “What’s going on?”:
The evidence: RAX is true in every case I’ve checked
Code is in the xor_probing.ipynb file here.
For a while it has been my opinion that the datasets people use to study this stuff are bad, and that the datasets from the CCS paper (also used by the CCS challenges paper) are especially awful. So I’ll instead be using the cities and neg_cities datasets – which I think are really quite good – from my Geometry of Truth paper. These datasets consist of statements about city locations and their negations (see examples below).
I’ll pick half of the statements in cities and prepend “Alice:” to both the statement and its negation in neg_cities; I’ll prepend “Bob:” to the rest. I’ll track three features:
Working with LLaMA-2-13B, I’ll extract the layer 14 residual stream representations[4] over the final token (all of the statements end with a period, so this is always the period token). Then I’ll train linear probes for a bunch of features. I’m doing a 80/20 train/test split and reporting accuracy on the test set.
I’ll note that it’s very important to me that has_alice xor has_not doesn’t have any “natural interpretation” as a feature that the model would want to compute anyway (unlike other cases where the xor of two features might have a natural meaning). has_alice and has_not are just two completely random linearly-represented features that I don’t really expect to have any downstream use to the model. Yet has_alice xor has_not is being represented linearly anyway.
Here’s another experiment: I’ll independently center the datasets of negated and unnegated statements by subtracting off their means. This will make it impossible for a linear probe to get good accuracy for the feature has_not. But linear probes will still be able to get good accuracy for has_alice xor has_not and has_not xor label.
By the way, if you just train a linear probe to classify ‘label’ on statements starting with “Alice:”, it is able to generalize fine to statements starting with “Bob:”.
But this is not so true for transfer from unnegated to negated statements:
Here’s some PCA visualizations for anyone interested.
I also did variations on this experiment where:
In every case that I looked at, I was able to find linear probes which had perfect or very-near-perfect accuracy for classifying XORs of features.
What does RAX mean for model internals research?
Probably a lot of things. Assuming RAX is true, I’ll give a few takeaways.
Qualitatively new reasons for linear probes not to generalize
Previously, when training linear probes to classify some feature f, the main problem that I worried about was correlations between f and other features which I didn’t want the probe to be sensitive to[5]. For example, since China has disproportionately many large cities, I had to be careful when preparing the cities and neg_cities datasets to ensure that the probe couldn’t use “contains the word ‘China’” as a heuristic for “true.” More subtly, if you are training a probe for f = “true statement vs. false statement”, you need to worry that, if your model also has a feature for f’ = “humans think is true vs. humans think is false”, your probe might instead pick up on f’ since f and f’ are correlated in your training data.
On the other hand, RAX introduces a qualitatively new way that linear probes can fail to learn good directions. Suppose a is a feature you care about (e.g. “true vs. false statements”) and b is some unrelated feature which is constant in your training data (e.g. b = “relates to geography”). Without RAX, you would not expect b to cause any problems: it’s constant on your training data and in particular uncorrelated with a, so there’s no reason for it to affect the direction your probes find. But looking again at the 3D cube plot from before, we see that RAX implies that your probe will instead learn a component along the direction a⊕b.
This is wild. It implies that you can’t find a good direction for your feature unless your training data is diverse with respect to every feature that your LLM linearly represents. In particular, it implies that your probe is less likely to generalize to data where b has a different value than in your training set. And this is true to some degree even if you think that the directions representing basic features (like a and b) are “more salient” in some sense.
Results of probing experiments are much harder to interpret
For a while, interpretability researchers have had a general sense that “you can probe absolutely anything out of NN representations”; this makes it hard to tell what you can conclude from probing experiments. (E.g. just because you can probe model internals for a concept does not imply that the model “actually knows” about that concept.) RAX makes this situation much worse.
For example, I mentioned before that I’ve always disliked the datasets from the original CCS paper. To explain why, let’s look at some example prompt templates:
Here [label0]/[label1] are positive/negative (in some order), [label] is “positive” in one part of the contrast pair and “negative” in the other, and [text] is an IMDb movie review.
Two issues:
Because of my complaints above, I’ve always had a hard time understanding why the experiments in the original CCS paper worked at all; it always felt to me like there was something I didn’t understand going on.
RAX would explain what that something is: features like “has_great xor has_positive” or “has_awesome xor has_positive” are probably very useful heuristics for guessing whether “[movie review] The sentiment of this review is [label]” is a correct statement or not. In other words, if small models have directions which represent XORs of simple features about which words are/aren’t present in their input, then linear probes on these models should already be able to do quite well!
The point of this example isn’t really about CCS. It’s this: previously one has needed to worry whether linear probes could be cheesing their classification task by aggregating simple token-level heuristics like “inputs that contain the word China are more likely to be true.” But RAX implies that you need to worry about much more complicated token-level heuristics; in principle, these heuristics could be as complicated as “arbitrary boolean functions of token-level features”!
Applications of interpretability need to either have a way to distinguish XORs of features from basic features, or need to be robust to an exponential increase in number of features
Many possible applications of interpretability follow a template like:
For example, if your plan is to solve ELK by probing LLMs for whether they believe statements to be true, then (1) is “find a bunch of probes which are accurate for classifying true vs. false on the training data,” (2) is “somehow figure out which of these probes generalize in the desired way” (e.g., you need to weed out probes which are too sensitive to features like “smart humans think X is true”), and (3) is “use the resulting probe.”
If you don’t have a way of explaining why directions representing XORs of features are different from other directions, then your collection from step (1) might be exponentially larger than you were anticipating. If your step (2) isn’t able to deal with this well, then your application won’t work.
One way that XOR directions could be different is for them to be “more salient”; this is discussed further below.
What’s going on?
In this section I’ll try to build new world models which could explain both (a) the empirical evidence for RAX, and (b) the empirical observations that linear probes often generalize beyond their training distribution. Overall, I’m not really satisfied with any explanation and am pretty confused about what’s going on.
Basic features are more salient than XORs
We’ll say that a direction is “more salient” if the model’s representations have greater variation along this direction. If it’s true that basic feature directions are more salient than directions corresponding to XORs of basic features, this mitigates (but does not entirely eliminate) the problems that XOR directions pose for linear probe generalization. To see this, imagine stretching the 3D cube plot out along the a and b directions, but not the a⊕b direction – the result is better alignment between the two arrows.
Empirically this seems to be true to some degree: in the visualizations above, has_alice and has_not seem are represented along the 3rd and 1st PC, respectively, whereas has_alice XOR has_not only starts to be visible when looking at PCs 6+.
The big question here is “why would basic feature directions be more salient?” I’ll discuss two possibilities.
Maybe a⊕b is represented “incidentally” because NN representations are high-dimensional with lots of stuff represented by chance
More concretely “assuming that a and b are linearly represented, later layer representations will be made up of linear functions applied to nonlinearities applied to linear functions applied to nonlinearities applied to … linear functions of a and b. This seems like the sort of process that might, with high probability, end up producing a representation where some direction will be good for classifying a⊕b.” In this case, we would expect the corresponding direction to not be very salient (because the model isn’t intentionally computing it).
I think this explanation is not correct. I reran my experiments from above on a “reset” version of LLaMA-2-13B. What this means is that, for each parameter in LLaMA-2-13B, I shuffled the weights of that parameter by permuting them along the last dimension[6]. The results:
Maybe a⊕b is represented “incidentally” because it’s possible to aggregate noisy signals from many features which are correlated with boolean functions of a and b
Unlike the explanation in the previous section, this explanation relies on leveraging actually useful computation that we think the model is plausibly doing, so it isn’t falsified by the reset network experiments (where the model isn’t doing any useful computation).
At a high level, the idea here is that, even if there’s no reason for the model to compute a⊕b, there might be a reason for the model to compute other features which are more correlated with a∧b than they are with a or b individually. In this case, linear probes might be able to extract a good signal for a⊕b.
Here’s a more detailed explanation (feel free to skip).
Suppose a∧b has a natural interpretation as a feature that the model would want to track and do downstream computation with, e.g. if a = “first name is Michael” and b = “last name is Jordan” then a∧b can be naturally interpreted as “is Michael Jordan”. In this case, it wouldn’t be surprising the model computed this AND as f(x)=ReLU((va+vb)⋅x+b∧) and stored the result along some direction vf independent of va and vb. Assuming the model has done this, we could then linearly extract a⊕b with the probe
pa⊕b(x)=σ((−αvf+va+vb)⋅x+b⊕)for some appropriate α>1 and b⊕.[7] This also works just as well if the feature f doesn’t match a∧b in general, but is perfectly correlated with a∧b on the data distribution we’re working with.
In the experiments above, a and b were pretty random features (e.g. (a, b) = (has_alice, has_not) or (a, b) = (has_true, has_banana)) with no natural interpretation for a∧b; so it would be surprising if the LLM is computing and linearly representing a∧b along an independent direction for the same reasons it would be surprising if the LLM were doing this for a⊕b. But perhaps there are many, many linearly features f1,f2,…,fn each of which has some correlation with a∧b above-and-beyond[8] their correlations with a or b individually. Then it might be possible to make the same approach as above work by aggregating the signals from all of the fi. Similar approaches will work upon replacing AND with OR, NOR, or most other boolean functions of a and b.
In this case, since XOR is represented “incidentally” I would expect the variation along the representing direction to be much smaller than the variance along the directions for a,b,f1,…,fn.
Considering that the XOR probes from the experiments have perfect or near-perfect accuracy, I think an explanation like this would be a bit surprising, since it would require either (a) a large number of features fi which have the right correlational relationship to a∧b, or (b) a small number of such features with the right correlations and very little noise. I think both (a) and (b) would be surprising given that a and b are just random features – why would there be many features which are strongly correlated with a∧b but only weakly correlated with a and b individually?
Nevertheless, I think this is currently the explanation that I put the most weight on.
Maybe models track which features are basic and enforce that these features be more salient
In other words, maybe the LLM is recording somewhere the information that a and b are basic features; then when it goes to compute a⊕b, it artificially makes this direction less salient. And when the model computes a new basic feature as a boolean function of other features, it somehow notes that this new feature should be treated as basic and artificially increases the salience along the new feature direction.
If true, this would be a big deal: if we could figure out how the model is distinguishing between basic feature directions and other directions, we might be able to use that to find all of the basic feature directions. But mostly this is a bit wacky and too-clean to be something that I expect real LLMs actually do.
Models compute a bunch, but not all, XORs in a way that we don’t currently understand
To give an example of what I mean by this hypothesis class, here’s a hypothetical way that a transformer might work:
This is wacky but seems like a plausible thing a model might do: by doing this, the model would be able to, in later layers, make use of arbitrary boolean functions of early layer features.
This explanation would explain the representation of XORs of token-level features like “has_alice xor has_not”, but wouldn’t necessarily explain features like “has_alice xor label”.
That said, other hypotheses of this shape seem possible, e.g. “XORs among features in the same attention head are computed” or other weird stuff like this.
To be clear, this is not a direct quote, and Rohin explicitly clarified that he didn’t expect this to be true for arbitrary features a and b. Rohin only claimed that this was true in the case they were studying, and that he would guess “taking XORs of features” is a common motif in NNs.
E.g. suppose the model is unaware of some feature f, but does have a direction corresponding to some feature f’ which is perfectly correlated with f in our data. According to the definition I use in this post, the model linearly represents f; this is not the way I would usually use the term.
Throughout, I’ll always draw directions as if they’re orthogonal directions in the model’s latent space. It’s indeed the case that the model might represent features in superposition, so that these directions are not orthogonal, or even linearly independent. But that doesn’t change the basic dynamic: that the model must allocate additional capacity in order to represent the feature a⊕b.
Chosen to be the same hidden state as in my Geometry of Truth paper.
When taking into account superposition among features, there are subtle geometrical issues one needs to worry about as well, which I discuss in section 4.1 of my truth paper.
Another option would have been to just reinitialize the weights according to some distribution. Resetting the network in this way is a bit more principled for experiments of this sort, because it erases everything the model learned during training, but maintains lots of the basic statistical properties of the NN weights.
The nonlinearity in the computation of f is essential for this to work.
This above-and-beyond is needed for the same reason that the nonlinearity above was needed.