This is a special post for quick takes by Thomas Kwa. Only they can create top-level comments. Comments here also appear on the Quick Takes page and All Posts page.
Thomas Kwa's Shortform
41Thomas Kwa
11ryan_greenblatt
9ryan_greenblatt
2Thomas Kwa
2ryan_greenblatt
3Daniel Kokotajlo
8gwern
2Thomas Kwa
2Thomas Kwa
37Thomas Kwa
14Buck
35Thomas Kwa
7Neel Nanda
7Thomas Kwa
3habryka
2Neel Nanda
16Thomas Kwa
7Thomas Kwa
15LawrenceC
5Thomas Kwa
1TsviBT
6Thomas Kwa
2Lauro Langosco
2TurnTrout
1Thomas Kwa
1Thomas Kwa
5Thomas Kwa
4Thomas Kwa
9Buck
2Chris_Leong
4Thomas Kwa
4Thomas Kwa
2leogao
2Thomas Kwa
Edit: Full post here with 9 domains and updated conclusions!
Cross-domain time horizon:
We know AI time horizons (human time-to-complete at which a model has a 50% success rate) on software tasks are currently ~1.5hr and doubling every 4-7 months, but what about other domains? Here's a preliminary result comparing METR's task suite (orange line) to benchmarks in other domains, all of which have some kind of grounding in human data:
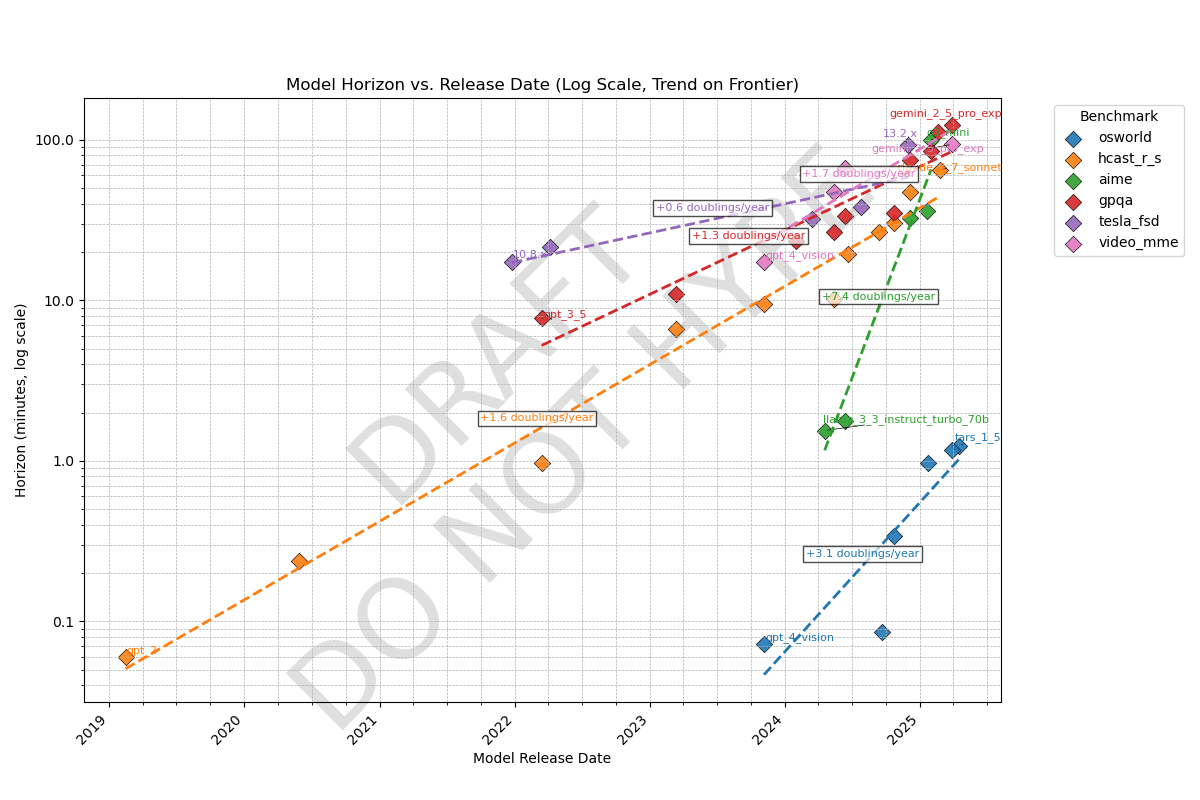
Observations
- Time horizons on agentic computer use (OSWorld) is ~100x shorter than other domains. Domains like Tesla self-driving (tesla_fsd), scientific knowledge (gpqa), and math contests (aime), video understanding (video_mme), and software (hcast_r_s) all have roughly similar horizons.
- My guess is this means models are good at taking in information from a long context but bad at acting coherently. Most work requires agency like OSWorld, which may be why AIs can't do the average real-world 1-hour task yet.
- There are likely other domains that fall outside this cluster; these are just the five I examined
- Note the original version had a unit conversion error that gave 60x too high horizons for video_mme; this has been fixed (thanks @ryan_greenblatt )
- Rate of improvement varies significantly; math contests have improved ~50x in the last year but Tesla self-driving only 6x in 3 years.
- HCAST is middle of the pack in both.
Note this is preliminary and uses a new methodology so there might be data issues. I'm currently writing up a full post!
Is this graph believable? What do you want to see analyzed?
edit: fixed Video-MME numbers
1but bad at acting coherently. Most work requires agency like OSWorld, which may be why AIs can't do the average real-world 1-hour task yet.
I'd have guessed that poor performance on OSWorld is mostly due to poor vision and mouse manipulation skills, rather than insufficient ability to act coherantly.
I'd guess that typical self-contained 1-hour task (as in, a human professional could do it in 1 hour with no prior context except context about the general field) also often require vision or non-text computer interaction and if they don't, I bet the AIs actually do pretty well.
1I'm skeptical and/or confused about the video MME results:
- You show Gemini 2.5 Pro's horizon length as ~5000 minutes or 80 hours. However, the longest videos in the benchmark are 1 hour long (in the long category they range from 30 min to 1 hr). Presumably you're trying to back out the 50% horizon length using some assumptions and then because Gemini 2.5 Pro's performance is 85%, you back out a 80-160x multiplier on the horizon length! This feels wrong/dubious to me if it is what you are doing.
- Based on how long these horizon lengths are, I'm guessing you assumed that answering a question about a 1 hour long video takes a human 1 hr. This seems very wrong to me. I'd bet humans can typically answer these questions much faster by panning through the video looking for where the question might be answered and then looking at just that part. Minimally, you can sometimes answer the question by skimming the transcript and it should be possible to watch at 2x/3x speed. I'd guess the 1 hour video tasks take more like 5-10 min for a well practiced human, and I wouldn't be surprised by much shorter.
- For this benchmark, (M)LLM performance seemingly doesn't vary much with video duration, invalidating that horizon length (at least horizon length based on video length) is a good measure on this dataset!
There was a unit conversion mistake, it should have been 80 minutes. Now fixed.
Besides that, I agree with everything here; these will all be fixed in the final blog post. I already looked at one of the 30m-1h questions and it appeared to be doable in ~3 minutes with the ability to ctrl-f transcripts but would take longer without transcripts, unknown how long.
In the next version I will probably use the no-captions AI numbers and measure myself without captions to get a rough video speed multiplier, then possibly do better stats that separate out domains with strong human-time-dependent difficulty from domains without (like this and SWE-Lancer).
No captions feels very unnatural because both llms and humans could first apply relatively dumb speech to text tools.
- Rate of improvement also varies significantly; math contests have improved ~50x in the last year but Tesla self-driving only 6x in 3 years.
I wish I had thought to blind myself to these results and try to predict them in advance. I think I would have predicted that Tesla self-driving would be the slowest and that aime would be the fastest. Not confident though.
(Solving difficult math problems is just about the easiest long-horizon task to train for,* and in the last few months we've seen OpenAI especially put a lot of effort into training this.)
*Only tokens, no images. Also no need for tools/plugins to the internet or some code or game environment. Also you have ground-truth access to the answers, it's impossible to reward hack.
I think I would have predicted that Tesla self-driving would be the slowest
For graphs like these, it obviously isn't important how the worst or mediocre competitors are doing, but the best one. It doesn't matter who's #5. Tesla self-driving is a longstanding, notorious failure. (And apparently is continuing to be a failure, as they continue to walk back the much-touted Cybertaxi launch, which keeps shrinking like a snowman in hell, now down to a few invited users in a heavily-mapped area with teleop.)
I'd be much more interested in Waymo numbers, as that is closer to SOTA, and they have been ramping up miles & cities.
I would love to have Waymo data. It looks like it's only available since September 2024 so I'll still need to use Tesla for the earlier period. More critically they don't publish disengagement data, only crash/injury. There are Waymo claims of things like 1 disengagement every 17,000 miles but I don't believe them without a precise definition for what this number represents.
New graph with better data, formatting still wonky though. Colleagues say it reminds them of a subway map.
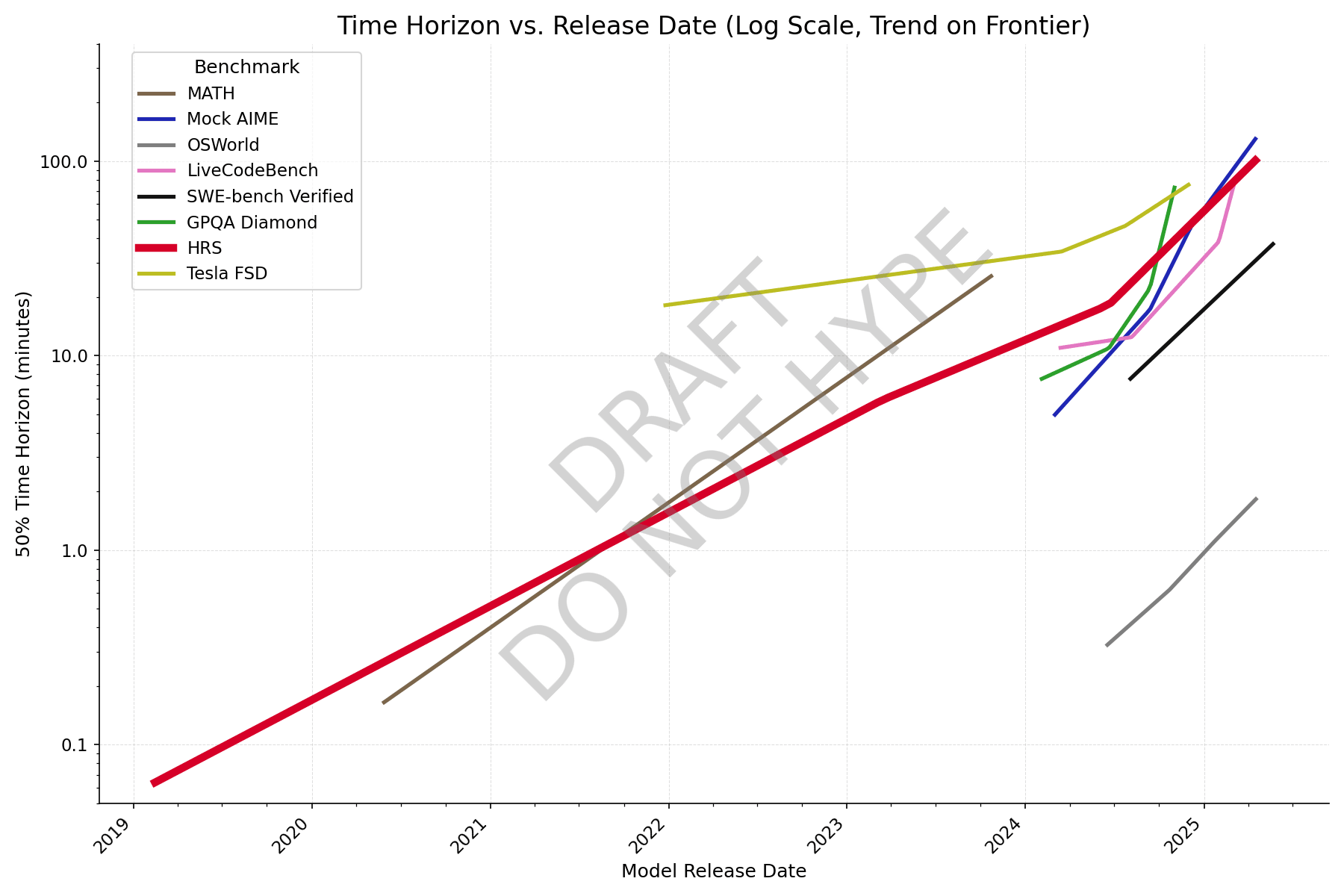
With individual question data from Epoch, and making an adjustment for human success rate (adjusted task length = avg human time / human success rate), AIME looks closer to the others, and it's clear that GPQA Diamond has saturated.
Some versions of the METR time horizon paper from alternate universes:
Measuring AI Ability to Take Over Small Countries (idea by Caleb Parikh)
Abstract: Many are worried that AI will take over the world, but extrapolation from existing benchmarks suffers from a large distributional shift that makes it difficult to forecast the date of world takeover. We rectify this by constructing a suite of 193 realistic, diverse countries with territory sizes from 0.44 to 17 million km^2. Taking over most countries requires acting over a long time horizon, with the exception of France. Over the last 6 years, the land area that AI can successfully take over with 50% success rate has increased from 0 to 0 km^2, at the rate of 0 km^2 per year (95% CI 0.0-0.0 km^2/year); extrapolation suggests that AI world takeover is unlikely to occur in the near future. To address concerns about the narrowness of our distribution, we also study AI ability to take over small planets and asteroids, and find similar trends.
Measuring AI Ability to Worry About AI
Abstract: Since 2019, the amount of time LW has spent worrying about AI has doubled every seven months, and now constitutes the primary bottleneck to AI safety research. Automation of worrying would be transformative to the research landscape, but worrying includes several complex behaviors, ranging from simple fretting to concern, anxiety, perseveration, and existential dread, and so is difficult to measure. We benchmark the ability of frontier AIs to worry about common topics like disease, romantic rejection, and job security, and find that current frontier models such as Claude 3.7 Sonnet already outperform top humans, especially in existential dread. If these results generalize to worrying about AI risk, AI systems will be capable of autonomously worrying about their own capabilities by the end of this year, allowing us to outsource all our AI concerns to the systems themselves.
Estimating Time Since The Singularity
Early work on the time horizon paper used a hyperbolic fit, which predicted that AGI (AI with an infinite time horizon) was reached last Thursday. [1] We were skeptical at first because the R^2 was extremely low, but recent analysis by Epoch suggested that AI already outperformed humans at a 100-year time horizon by about 2016. We have no choice but to infer that the Singularity has already happened, and therefore the world around us is a simulation. We construct a Monte Carlo estimate over dates since the Singularity and simulator intentions, and find that the simulation will likely be turned off in the next three to six months.
[1]: This is true
A few months ago, I accidentally used France as an example of a small country that it wouldn't be that catastrophic for AIs to take over, while giving a talk in France 😬
8
2Quick takes from ICML 2024 in Vienna:
- In the main conference, there were tons of papers mentioning safety/alignment but few of them are good as alignment has become a buzzword. Many mechinterp papers at the conference from people outside the rationalist/EA sphere are no more advanced than where the EAs were in 2022. [edit: wording]
- Lots of progress on debate. On the empirical side, a debate paper got an oral. On the theory side, Jonah Brown-Cohen of Deepmind proves that debate can be efficient even when the thing being debated is stochastic, a version of this paper from last year. Apparently there has been some progress on obfuscated arguments too.
- The Next Generation of AI Safety Workshop was kind of a mishmash of various topics associated with safety. Most of them were not related to x-risk, but there was interesting work on unlearning and other topics.
- The Causal Incentives Group at Deepmind developed a quantitative measure of goal-directedness, which seems promising for evals.
- Reception to my Catastrophic Goodhart paper was decent. An information theorist said there were good theoretical reasons the two settings we studied-- KL divergence and best-of-n-- behaved similarly.
- OpenAI gave a disappointing safety presentation at NGAIS touting their new technique of rules-based rewards, which is a variant of constitutional AI and seems really unambitious.
- The mechinterp workshop often had higher-quality papers than the main conference. It was completely full. Posters were right next to each other and the room was so packed during talks they didn't let people in.
- I missed a lot of the workshop, so I need to read some posters before having takes.
- My opinions on the state of published AI safety work:
- Mechinterp is progressing but continues to need feedback loops, either from benchmarks (I'm excited about people building on our paper InterpBench) or downstream tasks where mechinterp outperforms fine-tuning alone.
- Most of the danger from AI comes from goal-directed agents and instrumental convergence. There is little research now because we don't have agents yet. In 1-3 years, foundation model agents will be good enough to study, and we need to be ready with the right questions and theoretical frameworks.
- We still do not know enough about AI safety to make policy recommendations about specific techniques companies should apply.
4
2
1
1
1Mechinterp is often no more advanced than where the EAs were in 2022.
Seems pretty false to me, ICML just rejected a bunch of the good submissions lol. I think that eg sparse autoencoders are a massive advance in the last year that unlocks a lot of exciting stuff
3I agree, there were some good papers, and mechinterp as a field is definitely more advanced. What I meant to say was that many of the mechinterp papers accepted to the conference weren't very good.
Eight beliefs I have about technical alignment research
Written up quickly; I might publish this as a frontpage post with a bit more effort.
- Conceptual work on concepts like “agency”, “optimization”, “terminal values”, “abstractions”, “boundaries” is mostly intractable at the moment.
- Success via “value alignment” alone— a system that understands human values, incorporates these into some terminal goal, and mostly maximizes for this goal, seems hard unless we’re in a very easy world because this involves several fucked concepts.
- Whole brain emulation probably won’t happen in time because the brain is complicated and biology moves slower than CS, being bottlenecked by lab work.
- Most progress will be made using simple techniques and create artifacts publishable in top journals (or would be if reviewers understood alignment as well as e.g. Richard Ngo).
- The core story for success (>50%) goes something like:
- Corrigibility can in practice be achieved by instilling various cognitive properties into an AI system, which are difficult but not impossible to maintain as your system gets pivotally capable.
- These cognitive properties will be a mix of things from normal ML fields (safe RL), things that rhyme with normal ML fields (unlearning, faithfulness), and things that are currently conceptually fucked but may become tractable (low impact, no ontological drift).
- A combination of oversight and these cognitive properties is sufficient to get useful cognitive work out of an AGI.
- Good oversight complements corrigibility properties, because corrigibility both increases the power of your most capable trusted overseer and prevents your untrusted models from escaping.
- Most end-to-end “alignment plans” are bad for three reasons: because research will be incremental and we need to adapt to future discoveries, because we need to achieve several things for AI to go well (no alignment magic bullet), and because to solve the hardest worlds that are possible, you have to engage with MIRI threat models which very few people can do well [1].
- e.g. I expect Superalignment’s impact to mostly depend on their ability to adapt to knowledge about AI systems that we gain in the next 3 years, and continue working on relevant subproblems.
- The usefulness of basic science is limited unless you can eventually demonstrate some application. We should feel worse about a basic science program the longer it goes without application, and try to predict how broad the application of potential basic science programs will be.
- Glitch tokens work probably won’t go anywhere. But steering vectors are good because there are more powerful techniques in that space.
- The usefulness of sparse coding depends on whether we get applications like sparse circuit discovery, or intervening on features in order to usefully steer model behavior. Likewise with circuits-style mechinterp, singular learning theory, etc.
- There are convergent instrumental pressures towards catastrophic behavior given certain assumptions about how cognition works, but the assumptions are rather strong and it’s not clear if the argument goes through.
- The arguments I currently think are strongest are Alex Turner’s power-seeking theorem and an informal argument about goals.
- Thoughts on various research principles picked up from Nate Soares
- You should have a concrete task in mind when you’re imagining an AGI or alignment plan: agree. I usually imagine something like “Apollo program from scratch”.
- Non-adversarial principle (A safe AGI design should not become unsafe if any part of it becomes infinitely good at its job): unsure, definitely agree with weaker versions
- Garrabrant calls this robustness to relative scale
- To make any alignment progress we must first understand cognition through either theory or interpretability: disagree
- You haven’t engaged with the real problem until your alignment plan handles metacognition, self-modification, etc.: weakly disagree; wish we had some formalism for “weak metacognition” to test our designs against [2]
[1], [2]: I expect some but not all of the MIRI threat models to come into play. Like, when we put safeguards into agents, they'll rip out or circumvent some but not others, and it's super tricky to predict which. My research with Vivek often got stuck by worrying too much about reflection, others get stuck by worrying too little.
8
4
1You should update by +-1% on AI doom surprisingly frequently
This is just a fact about how stochastic processes work. If your p(doom) is Brownian motion in 1% steps starting at 50% and stopping once it reaches 0 or 1, then there will be about 50^2=2500 steps of size 1%. This is a lot! If we get all the evidence for whether humanity survives or not uniformly over the next 10 years, then you should make a 1% update 4-5 times per week. In practice there won't be as many due to heavy-tailedness in the distribution concentrating the updates in fewer events, and the fact you don't start at 50%. But I do believe that evidence is coming in every week such that ideal market prices should move by 1% on maybe half of weeks, and it is not crazy for your probabilities to shift by 1% during many weeks if you think about it often enough. [Edit: I'm not claiming that you should try to make more 1% updates, just that if you're calibrated and think about AI enough, your forecast graph will tend to have lots of >=1% week-to-week changes.]
1
11The general version of this statement is something like: if your beliefs satisfy the law of total expectation, the variance of the whole process should equal the variance of all the increments involved in the process.[1] In the case of the random walk where at each step, your beliefs go up or down by 1% starting from 50% until you hit 100% or 0% -- the variance of each increment is 0.01^2 = 0.0001, and the variance of the entire process is 0.5^2 = 0.25, hence you need 0.25/0.0001 = 2500 steps in expectation. If your beliefs have probability p of going up or down by 1% at each step, and 1-p of staying the same, the variance is reduced by a factor of p, and so you need 2500/p steps.
(Indeed, something like this standard way to derive the expected steps before a random walk hits an absorbing barrier).
Similarly, you get that if you start at 20% or 80%, you need 1600 steps in expectation, and if you start at 1% or 99%, you'll need 99 steps in expectation.
One problem with your reasoning above is that as the 1%/99% shows, needing 99 steps in expectation does not mean you will take 99 steps with high probability -- in this case, there's a 50% chance you need only one update before you're certain (!), there's just a tail of very long sequences. In general, the expected value of variables need not look like
I also think you're underrating how much the math changes when your beliefs do not come in the form of uniform updates. In the most extreme case, suppose your current 50% doom number comes from imagining that doom is uniformly distributed over the next 10 years, and zero after -- then the median update size per week is only 0.5/520 ~= 0.096%/week, and the expected number of weeks with a >1% update is 0.5 (it only happens when you observe doom). Even if we buy a time-invariant random walk model of belief updating, as the expected size of your updates get larger, you also expect there to be quadratically fewer of them -- e.g. if your updates came in increments of size 0.1 instead of 0.01, you'd expect only 25 such updates!
Applying stochastic process-style reasoning to beliefs is empirically very tricky, and results can vary a lot based on seemingly reasonable assumptions. E.g. I remember Taleb making a bunch of mathematically sophisticated arguments[2] that began with "Let your beliefs take the form of a Wiener process[3]" and then ending with an absurd conclusion, such as that 538's forecasts are obviously wrong because their updates aren't Gaussian distributed or aren't around 50% until immediately before the elction date. And famously, reasoning of this kind has often been an absolute terrible idea in financial markets. So I'm pretty skeptical of claims of this kind in general.
- ^
There's some regularity conditions here, but calibrated beliefs that things you eventually learn the truth/falsity of should satisfy these by default.
- ^
Often in an attempt to Euler people who do forecasting work but aren't super mathematical, like Philip Tetlock.
- ^
This is what happens when you take the limit of the discrete time random walk, as you allow for updates on ever smaller time increments. You get Gaussian distributed increments per unit time -- W_t+u - W_t ~ N(0, u) -- and since the tail of your updates is very thin, you continue to get qualitatively similar results to your discrete-time random walk model above.
And yes, it is ironic that Taleb, who correctly points out the folly of normality assumptions repeatedly, often defaults to making normality assumptions in his own work.
2I talked about this with Lawrence, and we both agree on the following:
- There are mathematical models under which you should update >=1% in most weeks, and models under which you don't.
- Brownian motion gives you 1% updates in most weeks. In many variants, like stationary processes with skew, stationary processes with moderately heavy tails, or Brownian motion interspersed with big 10%-update events that constitute <50% of your variance, you still have many weeks with 1% updates. Lawrence's model where you have no evidence until either AI takeover happens or 10 years passes does not give you 1% updates in most weeks, but this model is almost never the case for sufficiently smart agents.
- Superforecasters empirically make lots of little updates, and rounding off their probabilities to larger infrequent updates make their forecasts on near-term problems worse.
- Thomas thinks that AI is the kind of thing where you can make lots of reasonable small updates frequently. Lawrence is unsure if this is the state that most people should be in, but it seems plausibly true for some people who learn a lot of new things about AI in the average week (especially if you're very good at forecasting).
- In practice, humans often update in larger discrete chunks. Part of this is because they only consciously think about new information required to generate new numbers once in a while, and part of this is because humans have emotional fluctuations which we don't include in our reported p(doom).
- Making 1% updates in most weeks is not always just irrational emotional fluctuations; it is consistent with how a rational agent would behave under reasonable assumptions. However, we do not recommend that people consciously try to make 1% updates every week, because fixating on individual news articles is not the right way to think about forecasting questions, and it is empirically better to just think about the problem directly rather than obsessing about how many updates you're making.
Probabilities on summary events like this are mostly pretty pointless. You're throwing together a bunch of different questions, about which you have very different knowledge states (including how much and how often you should update about them).
I'm worried that "pause all AI development" is like the "defund the police" of the alignment community. I'm not convinced it's net bad because I haven't been following governance-- my current guess is neutral-- but I do see these similarities:
- It's incredibly difficult and incentive-incompatible with existing groups in power
- There are less costly, more effective steps to reduce the underlying problem, like making the field of alignment 10x larger or passing regulation to require evals
- There are some obvious negative effects; potential overhangs or greater incentives to defect in the AI case, and increased crime, including against disadvantaged groups, in the police case
- There's far more discussion than action (I'm not counting the fact that GPT5 isn't being trained yet; that's for other reasons)
- It's memetically fit, and much discussion is driven by two factors that don't advantage good policies over bad policies, and might even do the reverse. This is the toxoplasma of rage.
- disagreement with the policy
- (speculatively) intragroup signaling; showing your dedication to even an inefficient policy proposal proves you're part of the ingroup. I'm not 100% this was a large factor in "defund the police" and this seems even less true with the FLI letter, but still worth mentioning.
This seems like a potentially unpopular take, so I'll list some cruxes. I'd change my mind and endorse the letter if some of the following are true.
- The claims above are mistaken/false somehow.
- Top labs actually start taking beneficial actions towards the letter's aims
- It's caused people to start thinking more carefully about AI risk
- A 6 month pause now is especially important by setting anti-racing norms, demonstrating how far AI alignment is lagging behind capabilities, or something
- A 6 month pause now is worth close to 6 months of alignment research at crunch time (my guess is that research at crunch time is worth 1.5x-3x more depending on whether MIRI is right about everything)
- The most important quality to push towards in public discourse is how much we care about safety at all, so I should endorse this proposal even though it's flawed
11There are less costly, more effective steps to reduce the underlying problem, like making the field of alignment 10x larger or passing regulation to require evals
IMO making the field of alignment 10x larger or evals do not solve a big part of the problem, while indefinitely pausing AI development would. I agree it's much harder, but I think it's good to at least try, as long as it doesn't terribly hurt less ambitious efforts (which I think it doesn't).
It's incredibly difficult and incentive-incompatible with existing groups in power
Why does this have to be true? Can't governments just compensate existing AGI labs for the expected commercial value of their foregone future advances due to indefinite pause?
This seems good if it could be done. But the original proposal was just a call for labs to individually pause their research, which seems really unlikely to work.
Also, the level of civilizational competence required to compensate labs seems to be higher than for other solutions. I don't think it's a common regulatory practice to compensate existing labs like this, and it seems difficult to work out all the details so that labs will feel adequately compensated. Plus there might be labs that irrationally believe they're undervalued. Regulations similar to the nuclear or aviation industry feel like a more plausible way to get slowdown, and have the benefit that they actually incentivize safety work.
I now think the majority of impact of AI pause advocacy will come from the radical flank effect, and people should study it to decide whether pause advocacy is good or bad.
The independent-steps model of cognitive power
A toy model of intelligence implies that there's an intelligence threshold above which minds don't get stuck when they try to solve arbitrarily long/difficult problems, and below which they do get stuck. I might not write this up otherwise due to limited relevance, so here it is as a shortform, without the proofs, limitations, and discussion.
The model
A task of difficulty n is composed of independent and serial subtasks. For each subtask, a mind of cognitive power knows different “approaches” to choose from. The time taken by each approach is at least 1 but drawn from a power law, for , and the mind always chooses the fastest approach it knows. So the time taken on a subtask is the minimum of samples from the power law, and the overall time for a task is the total for the n subtasks.
Main question: For a mind of strength ,
- what is the average rate at which it completes tasks of difficulty n?
- will it be infeasible for it to complete sufficiently large tasks?
Results
- There is a critical threshold of intelligence below which the distribution of time to complete a subtask has infinite mean. This threshold depends on .
- This implies that for an n-step task, the median of average time-per-subtask grows without bound as n increases. So (for minds below the critical threshold) the median time to complete a whole task grows superlinearly with n.
- Above the critical threshold, minds can solve any task in expected linear time.
- Some distance above the critical threshold, minds are running fairly close to the optimal speed, and further increases in Q cause small efficiency gains.
- I think this doesn't depend on the function being a power law; it would be true for many different heavy-tailed distributions, but the math wouldn't be as nice.
In terms of developing better misalignment risk countermeasures, I think the most important questions are probably:
- How to evaluate whether models should be trusted or untrusted: currently I don't have a good answer and this is bottlenecking the efforts to write concrete control proposals.
- How AI control should interact with AI security tools inside labs.
More generally:
- How can we get more evidence on whether scheming is plausible?
- How scary is underelicitation? How much should the results about password-locked models or arguments about being able to generate small numbers of high-quality labels or demonstrations affect this?
"How can we get more evidence on whether scheming is plausible?" - What if we ran experiments where we included some pressure towards scheming (either RL or fine-tuning) and we attempted to determine the minimum such pressure required to cause scheming? We could further attempt to see how this interacts with scaling.
I started a dialogue with @Alex_Altair a few months ago about the tractability of certain agent foundations problems, especially the agent-like structure problem. I saw it as insufficiently well-defined to make progress on anytime soon. I thought the lack of similar results in easy settings, the fuzziness of the "agent"/"robustly optimizes" concept, and the difficulty of proving things about a program's internals given its behavior all pointed against working on this. But it turned out that we maybe didn't disagree on tractability much, it's just that Alex had somewhat different research taste, plus thought fundamental problems in agent foundations must be figured out to make it to a good future, and therefore working on fairly intractable problems can still be necessary. This seemed pretty out of scope and so I likely won't publish.
Now that this post is out, I feel like I should at least make this known. I don't regret attempting the dialogue, I just wish we had something more interesting to disagree about.
1I'm planning to write a post called "Heavy-tailed error implies hackable proxy". The idea is that when you care about and are optimizing for a proxy , Goodhart's Law sometimes implies that optimizing hard enough for causes to stop increasing.
A large part of the post would be proofs about what the distributions of and must be for , where X and V are independent random variables with mean zero. It's clear that
- X must be heavy-tailed (or long-tailed or something)
- X must have heavier tails than V
The proof seems messy though; Drake Thomas and I have spent ~5 person-days on it and we're not quite done. Before I spend another few days proving this, is it a standard result in statistics? I looked through a textbook and none of the results were exactly what I wanted.
Note that a couple of people have already looked at it for ~5 minutes and found it non-obvious, but I suspect it might be a known result anyway on priors.
Doesn't answer your question, but we also came across this effect in the RM Goodharting work, though instead of figuring out the details we only proved that it when it's definitely not heavy tailed it's monotonic, for Regressional Goodhart (https://arxiv.org/pdf/2210.10760.pdf#page=17). Jacob probably has more detailed takes on this than me.
In any event my intuition is this seems unlikely to be the main reason for overoptimization - I think it's much more likely that it's Extremal Goodhart or some other thing where the noise is not independent
We might want to keep our AI from learning a certain fact about the world, like particular cognitive biases humans have that could be used for manipulation. But a sufficiently intelligent agent might discover this fact despite our best efforts. Is it possible to find out when it does this through monitoring, and trigger some circuit breaker?
Evals can measure the agent's propensity for catastrophic behavior, and mechanistic anomaly detection hopes to do better by looking at the agent's internals without assuming interpretability, but if we can measure the agent's beliefs, we can catch the problem earlier. Maybe there can be more specific evals we give to the agent, which are puzzles that can only be solved if the agent knows some particular fact. Or maybe the agent is factorable into a world-model and planner, and we can extract whether it knows the fact from the world-model.
Have the situational awareness people already thought about this? Does anything change when we're actively trying to erase a belief?
Curated and popular this week