Suppose random variables and $X_{2}$ contain approximately the same information about a third random variable $Λ$ , i.e. both of the following diagrams are satisfied to within approximation $ϵ$ :

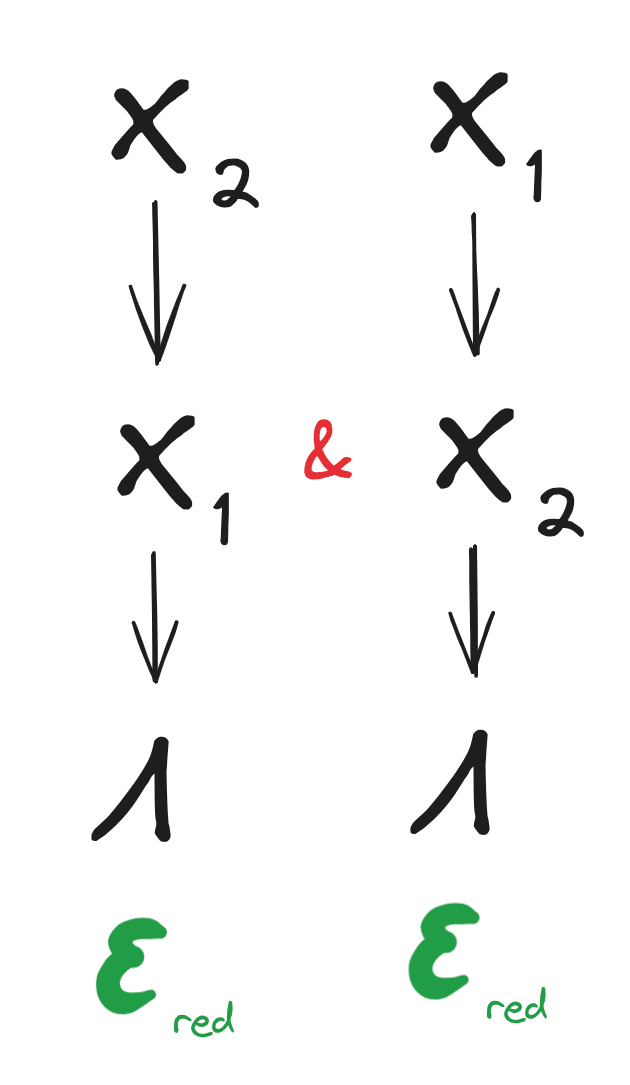
We call $Λ$ a "redund" over $X_{1}, X_{2}$ , since conceptually, any information $Λ$ contains about $X$ must be redundantly represented in both $X_{1}$ and $X_{2}$ (to within approximation).

Here's an intuitive claim which is surprisingly tricky to prove: suppose we construct a new variable $Λ^{'}$ by sampling from $P [Λ | X_{2}]$ , so the new joint distribution is

$P [X_{1} = x_{1}, X_{2} = x_{2}, Λ^{'} = λ^{'}] = P [X_{1} = x_{1}, X_{2} = x_{2}] P [Λ = λ^{'} | X_{2} = x_{2}]$

By construction, this "resampled" variable satisfies one of the two redundancy diagrams perfectly: $X_{1} \to X_{2} \to Λ^{'}$ . Intuitively, we might expect that $Λ^{'}$ approximately satisfies the other redundancy diagram as well; conceptually, $Λ^{'}$ (approximately) only contains redundant information about $X$ , so $X_{2}$ contains (approximately) the same information about $Λ^{'}$ as $X$ does, so the resampling operation should result in (approximately, in some sense) the same distribution we started with and therefore (approximately) the same properties.

In this post, we'll prove that claim and give a bound for the approximation error.

Specifically:

Theorem: Resampling (Approximately) Conserves (Approximate) Redundancy

Let random variables $X_{1}, X_{2}$ , $Λ$ satisfy the diagrams $X_{1} \to X_{2} \to Λ$ and $X_{2} \to X_{1} \to Λ$ to within $ϵ$ , i.e.

$ϵ \geq D_{K L} (P [X_{1}, X_{2}, Λ] | | P [X_{1}, X_{2}] P [Λ | X_{2}])$

$ϵ \geq D_{K L} (P [X_{1}, X_{2}, Λ] | | P [X_{1}, X_{2}] P [Λ | X_{1}])$

Also, assume $P [X, Λ] > 0$ .

Construct $Λ^{'}$ by sampling from $P [Λ | X_{2}]$ , so $P [X_{1}, X_{2}, Λ^{'}] = P [X_{1}, X_{2}] P [Λ = λ^{'} | X_{2}]$ . Then $X_{1} \to X_{2} \to Λ^{'}$ is perfectly satisfied by construction, and $X_{2} \to X_{1} \to Λ^{'}$ is satisfied to within $9 ϵ$ , i.e.

$9 ϵ \geq D_{K L} (P [X_{1}, X_{2}, Λ^{'}] | | P [X_{1}, X_{2}] P [Λ^{'} | X_{1}])$

In diagrammatic form:

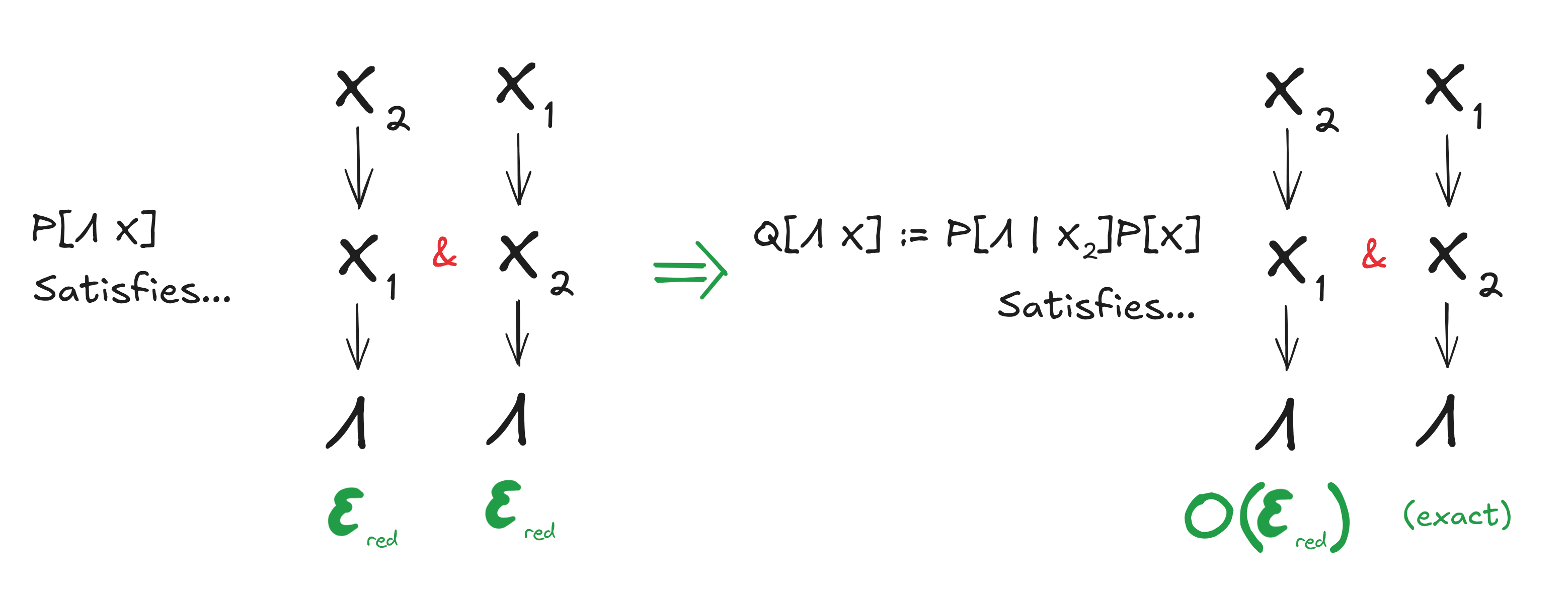
(Where O(Ɛ) in this version of the proof is 9Ɛ, specifically.)

Notation

We will use the shorthand $D_{K L} (< diagram over X >)$ to mean $D_{K L} (P [X] | | \prod_{i} P [X_{i} | X_{p a (i)}])$ . For instance, $D_{K L} (X_{1} \to X_{2} \to Λ)$ is shorthand for $D_{K L} (P [X_{1}, X_{2}, Λ] | | P [X_{1}] P [X_{2} | X_{1}] P [Λ | X_{2}])$ , which is equivalent to $D_{K L} (P [X, Λ] | | P [X] P [Λ | X_{2}])$ .

We will work with nats for mathematical convenience (i.e. all logarithms are natural logs).

Proof

The proof proceeds in three steps:

From $Λ$ , we can construct a new variable $Γ$ which is equal to $Λ$ with probability $p$ and is otherwise a constant. Then the errors on all diagrams in the theorem for $Γ$ are the same as the corresponding errors for $Λ$ , but scaled down by factor $p$ . This allows us to focus only on the regime of arbitrarily small errors, and obtain a global bound from that regime.
Within the regime of arbitrarily small errors, $D_{K L} (P | | Q)$ is approximately (to second order) equal to twice the Hellinger distance, $2 \sum_{X} (\sqrt{P [X]} - \sqrt{Q [X]})^{2}$ . Hellinger distance is a straightforward Euclidean distance metric, so we can use standard geometric reasoning on it.
The Hellinger distance between $P [Λ | X_{2}]$ and $P [Λ | X]$ , between $P [Λ | X]$ and $P [Λ | X_{1}]$ , and between $P [Λ | X_{1}]$ and $P [Λ^{'} | X_{1}]$ are all small, so end-to-end the Hellinger distance between $P [Λ | X_{2}]$ and $P [Λ^{'} | X_{1}]$ is small. That yields the bound we're after.

Step 1: Scaling Down The Errors

First we construct the new variable $Γ$ as a stochastic function of $Λ$ . Specifically, $Γ$ $= Λ$ with probability $p$ , else $Γ$ is a constant $C$ , where $C$ is outside the support of $Λ$ (so when we see $Γ = C$ , we gain no information about $Λ$ ).

A little algebra confirms that $Γ$ 's errors are simply $Λ$ 's errors scaled down by $p$ :

$D_{K L} (P [X, Γ] | | P [X] P [Γ | X_{i}])$

$= E_{X} [P [Γ = C] (l n P [Γ = C | X] - l n P [Γ = C | X_{i}]) + \sum_{λ} P [Γ = λ | X] (l n P [Γ = λ | X] - l n P [Γ = λ | X_{i}])]$

$= E_{X} [(1 - p) (l n (1 - p) - l n (1 - p)) + \sum_{λ} p P [Λ = λ | X] (l n (p P [Λ = λ | X]) - l n (p P [Λ = λ | X_{i}]))]$

$= p E_{X} [\sum_{λ} P [Λ = λ | X] (l n (P [Λ = λ | X]) - l n (P [Λ = λ | X_{i}]))]$

$= p D_{K L} (P [X, Λ] | | P [X] P [Λ | X_{i}])$

Similarly, constructing $Γ^{'}$ just like $Λ^{'}$ (i.e. $P [X, Γ^{'}] = P [X] P [Γ = γ^{'} | X_{2}]$ ) is equivalent to constructing $Γ^{'}$ as a stochastic function of $Λ^{'}$ where $Γ^{'} = Λ^{'}$ with probability $p$ , else $Γ^{'}$ is $C$ . So, by the same algebra as above,

$D_{K L} (P [X, Γ^{'}] | | P [X] P [Γ^{'} | X_{i}]) = p D_{K L} (P [X, Λ^{'}] | | P [X] P [Λ^{'} | X_{i}])$

The upshot: if there exists a distribution over variables $X_{1}, X_{2}, Λ$ for which

$D_{K L} (X_{2} \to X_{1} \to Λ^{'}) > n \cdot max (D_{K L} (X_{1} \to X_{2} \to Λ), D_{K L} (X_{2} \to X_{1} \to Λ))$

then there also exists a distribution satisfying the same inequality with all $D_{K L}$ 's arbitrarily small^[1]. Flipping that statement around: if there does not exist any distribution for which the $D_{K L}$ 's are all arbitrarily small and the inequality is satisfied, then there does not exist any distribution for which the inequality is satisfied.

In other words: if we can show

$D_{K L} (X_{2} \to X_{1} \to Λ^{'}) \leq n \cdot max (D_{K L} (X_{1} \to X_{2} \to Λ), D_{K L} (X_{2} \to X_{1} \to Λ)) \leq n ϵ$

in the regime where all the $D_{K L}$ 's are arbitrarily small, then the same inequality is also established globally, proving our theorem. The rest of the proof will therefore show

$D_{K L} (X_{2} \to X_{1} \to Λ^{'}) \leq n \cdot max (D_{K L} (X_{1} \to X_{2} \to Λ), D_{K L} (X_{2} \to X_{1} \to Λ))$

in the regime where all the $D_{K L}$ 's are arbitrarily small. In particular, we'll use a second order approximation for the $D_{K L}$ 's.

Step 2: Second Order Approximation

Validity

Before we can use a second order approximation of the $D_{K L}$ 's, we need to show that small $D_{K L}$ implies that second order approximationis valid.

For that purpose, we use the Hellinger-KL inequality:

$D (P | | Q) \geq 2 l n \frac{2}{2 - H^{2} (P, Q)}$

where $H^{2} (P, Q) := \sum_{X} (\sqrt{P [X]} - \sqrt{Q [X]})^{2}$ is the squared Hellinger distance.^[2]

Using standard logarithm inequalities, we can weaken the Hellinger-KL inequality to

$D (P | | Q) \geq H^{2} (P, Q)$

So, as $D_{K L} (P | | Q)$ goes to 0, the Hellinger distance goes to 0, and therefore $\sqrt{P}$ and $\sqrt{Q}$ are arbitrarily close together in standard Euclidean distance. Since $D_{K L}$ is smooth (for strictly positive distributions, which we have assumed), we can therefore use a second order approximation (with respect to $\sqrt{P} - \sqrt{Q}$ ) for our arbitrarily small $D_{K L}$ 's.

Expansion

Now for the second order expansion itself.

Our small quantity is $δ [X] := \sqrt{P [X]} - \sqrt{Q [X]}$ . Then

$D_{K L} (P | | Q) = \sum_{X} P [X] (l n P [X] - 2 l n \sqrt{Q [X]})$

$= \sum_{X} P [X] (l n P [X] - 2 l n (\sqrt{P [X]} - δ [X]))$

$= \sum_{X} P [X] (l n P [X] - 2 l n (\sqrt{P [X]}) + 2 \frac{δ [X]}{\sqrt{P [X]}} + 2 \frac{1}{2} (\frac{δ [X]}{\sqrt{P [X]}})^{2}) + o (δ^{3})$

$= \sum_{X} 2 \sqrt{P [X]} δ [X] + δ [X]^{2} + o (δ^{3})$

To simplify that further, we can use the sum-to-1 constraints on the distributions: $\sqrt{Q [X]} = \sqrt{P [X]} - δ [X]$ implies

$\sum_{X} Q [X] = \sum_{X} (\sqrt{P [X]} - δ [X])^{2} = \sum_{X} P [X] - 2 \sqrt{P [X]} δ [X] + δ [X]^{2}$

so $\sum_{X} 2 \sqrt{P [X]} δ [X] = \sum_{X} δ [X]^{2}$ . That simplifies our second order approximation to

$D_{K L} (P | | Q) = 2 \sum_{X} δ [X]^{2} + o (δ^{3})$

$= 2 \sum_{X} (\sqrt{P [X]} - \sqrt{Q [X]})^{2} + o (δ^{3})$

i.e. in the second order regime $D_{K L}$ is twice the Hellinger distance.

Combining this with Step 1, we've now established that if we can prove our desired bound for Hellinger distances rather than $D_{K L}$ , then the bound also applies globally for $D_{K L}$ errors. So now, we can set aside the notoriously finicky KL divergences, and work with good ol' Euclidean geometry.

Step 3: Good Ol' Euclidean Geometry

Writing everything out in the second order regime, our preconditions say

$ϵ \geq 2 E_{X} [\sum_{Λ} (\sqrt{P [Λ | X]} - \sqrt{P [Λ | X_{2}]})^{2}]$

$ϵ \geq 2 E_{X} [\sum_{Λ} (\sqrt{P [Λ | X]} - \sqrt{P [Λ | X_{1}]})^{2}]$

and we want to bound

$2 E_{X} [{\sum_{Λ}}_{Λ}^{'} (\sqrt{P [Λ^{'} | X]} - \sqrt{P [Λ^{'} | X_{1}]})^{2}]$

$= 2 E_{X} [\sum_{Λ} (\sqrt{P [Λ | X_{2}]} - \sqrt{\sum_{X_{2}^{'}} P [Λ | X_{2}^{'}] P [X_{2}^{'} | X_{1}]})^{2}]$

That last expression has a Jensen vibe to it, so let's use Jensen's inequality.

Jensen

We're going to use Jensen's inequality on the squared Hellinger distance, so we need to establish that squared Hellinger distance is convex as a function of the distributions $P, Q$ .

Differentiating $(\sqrt{p} - \sqrt{q})^{2}$ twice with respect to $(p, q)$ yields the Hessian

$\frac{1}{2} \frac{1}{\sqrt{p q}} (\begin{matrix} \frac{q}{p} & - 1 - 1 & \frac{p}{q} \end{matrix})$

Note that one column is the other column multiplied by $- \frac{p}{q}$ , so one of the eigenvalues is 0. The trace is positive, so the other eigenvalue is positive. Thus, the function is (non-strictly) convex.

Now, we'll use Jensen's inequality on

$ϵ \geq E_{X} [\sum_{Λ} (\sqrt{P [Λ | X]} - \sqrt{P [Λ | X_{2}]})^{2}]$

Specifically:

We'll hold $X_{1}$ constant, so it's not involved in our application of Jensen.
For each $X_{1}$ value, the expression takes a convex combination with weights $P [X_{2} | X_{1}]$ of the function $\sum_{Λ} (\sqrt{P [Λ | X]} - \sqrt{P [Λ | X_{2}]})^{2}$ .
Viewing $(P [Λ | X], P [Λ | X_{2}])$ at fixed $X_{1}$ as the function's inputs, the function is convex.

So, applying Jensen's, we get

$ϵ \geq 2 E_{X} [\sum_{Λ} (\sqrt{P [Λ | X]} - \sqrt{P [Λ | X_{2}]})^{2}]$

$\geq 2 E_{X_{1}} [\sum_{Λ} (\sqrt{\sum_{X_{2}} P [Λ | X] P [X_{2} | X_{1}]} - \sqrt{\sum_{X_{2}} P [Λ | X_{2}] P [X_{2} | X_{1}]})^{2}]$

$= 2 E_{X_{1}} [\sum_{Λ} (\sqrt{P [Λ | X_{1}]} - \sqrt{\sum_{X_{2}} P [Λ | X_{2}] P [X_{2} | X_{1}]})^{2}]$

$= 2 E_{X} [\sum_{Λ} (\sqrt{P [Λ | X_{1}]} - \sqrt{\sum_{X_{2}} P [Λ | X_{2}] P [X_{2} | X_{1}]})^{2}]$

Euclidean Distances

With that, we have bounds on three (squared) Hellinger distances:

$ϵ \geq 2 E_{X} [\sum_{Λ} (\sqrt{P [Λ | X]} - \sqrt{P [Λ | X_{2}]})^{2}]$

$ϵ \geq 2 E_{X} [\sum_{Λ} (\sqrt{P [Λ | X]} - \sqrt{P [Λ | X_{1}]})^{2}]$

$ϵ \geq 2 E_{X} [\sum_{Λ} (\sqrt{P [Λ | X_{1}]} - \sqrt{\sum_{X_{2}} P [Λ | X_{2}] P [X_{2} | X_{1}]})^{2}]$

So, on average over $X$ :

The Euclidean distance between $\sqrt{P [Λ | X_{2}]}$ and $\sqrt{P [Λ | X]}$ is at most $\sqrt{\frac{ϵ}{2}}$ .
The Euclidean distance between $\sqrt{P [Λ | X]}$ and $\sqrt{P [Λ | X_{1}]}$ is at most $\sqrt{\frac{ϵ}{2}}$ .
The Euclidean distance between $\sqrt{P [Λ | X_{1}]}$ and $\sqrt{\sum_{X_{2}} P [Λ | X_{2}] P [X_{2} | X_{1}]}$ is at most $\sqrt{\frac{ϵ}{2}}$ .

So, on average, the Euclidean distance from end-to-end, between $\sqrt{P [Λ | X_{2}]}$ and $\sqrt{\sum_{X_{2}} P [Λ | X_{2}] P [X_{2} | X_{1}]}$ , is at most $3 \sqrt{\frac{ϵ}{2}}$ .

That gives us the desired bound:

$(3 \sqrt{\frac{ϵ}{2}})^{2} \geq E_{X} [\sum_{Λ} (\sqrt{P [Λ | X_{2}]} - \sqrt{\sum_{X_{2}^{'}} P [Λ | X_{2}^{'}] P [X_{2}^{'} | X_{1}]})^{2}]$

implying

$9 ϵ \geq 2 E_{X} [\sum_{Λ} (\sqrt{P [Λ | X_{2}]} - \sqrt{\sum_{X_{2}^{'}} P [Λ | X_{2}^{'}] P [X_{2}^{'} | X_{1}]})^{2}]$

Combined with our previous two sections, that establishes the desired upper bound of $9 ϵ$ on $D_{K L} (X_{2} \to X_{1} \to Λ^{'})$ .

Empirical Results and Room for Improvement

Below is a plot of the maximal error achieved via numerical minimization of $- D_{K L} (X_{2} \to X_{1} \to Λ^{'})$ subject to a constraint on $D_{K L} (X_{1} \to X_{2} \to Λ) + D_{K L} (X_{2} \to X_{1} \to Λ)$ , searching over distributions of X and $Λ$ . Above, we proved that the ratio of those two quantities can be no higher than $\frac{9}{2}$ . As expected from the proof, it is visually clear that each point on the curve lies on a line between itself and the origin which itself always lies below the curve. Some, presumably, noise is present due to occasional failures of the optimizer to find the maximum error.

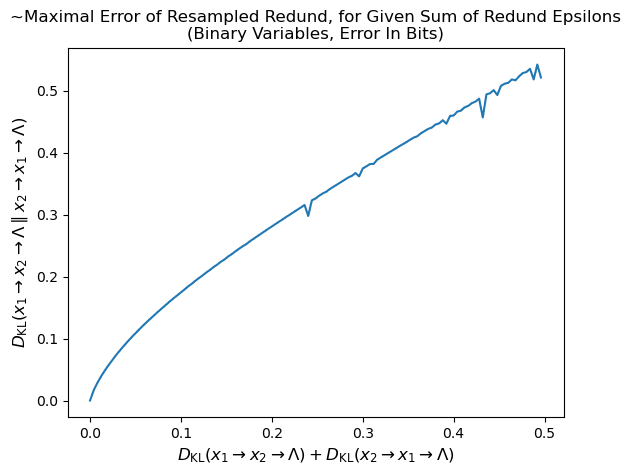
Zooming in on the steepest part of the curve and eyeballing the plot, it looks like the maximum ratio achieved is around 4 (.02/.005), implying an empirical upper bound of the resampled diagram of ~8 $ϵ$ :

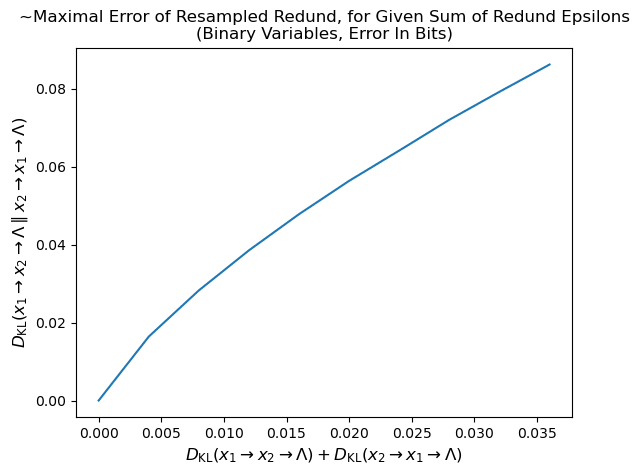
Looking into the actual solutions found, the solutions with ratio of ~4 involve one of the two terms in the x-axis sum being much larger than the other (5-10x). Therefore we expect to be able, in principle, to get a tighter bound (~4 $ϵ$ , empirically, rather than the proven 9 $ϵ$ or empirical 8 $ϵ$ .) The most likely place for improvement in the proof is to bound the Hellinger distance between $P [Λ | X_{1}]$ and $P [Λ | X_{2}]$ directly by $ϵ$ , cutting one step out of the "path", and that would indeed reduce the bound from 9 $ϵ$ to 4 $ϵ$ . We'll leave that for future work.

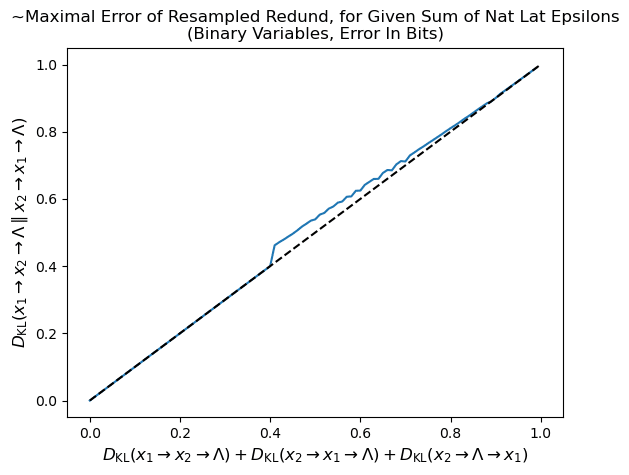
Interesting additional piece for future reference: If we include the mediation condition into the denominator, and so look for a bound in terms of a factor of the sum of all natural latent condition epsilons, we find that the empirical factor in question is 1 (roughly. Not sure what happened at ~0.4):

^{^}
Note that, since $P [X, Λ] > 0$ by assumption, none of the $D_{K L}$ 's are infinite. This is the only place where we need $P [X, Λ] > 0$ ; that assumption can probably be eliminated by considering the infinite case directly, but we're not going to do that here.
^{^}
A quick aside: while it might look messy at first, the Hellinger distance is a particularly natural way to talk about Euclidean distances between probability distributions. In general, if one wants to view a distribution $P [X]$ as a vector, $\sqrt{P [X]}$ is the most natural vector to consider, since the sum-to-1 constraint says $\sqrt{P [X]}$ is a unit vector under the standard Euclidean distance.

27

Resampling Conserves Redundancy (Approximately)

27