I'm having a bit of difficulty understanding the exact task/set up of this post, and so I have a few questions.
Here's a summary of your post as I understand it:
- In Anthropic's Toy Model of Attention Head "Superposition",[1] they consider a task where the model needs to use interference between heads to implement multiple skip trigrams. In particular, they consider, and call this "OV-incoherent, because the OV seems to need to use information "not present" in V of the source token. (This was incorrect, because you can implement their task perfectly using only a copying head and a negative copying head.) They call this attention head superposition because they didn't understand the algorithm, and so mistakenly thought they needed more attention heads than you actually need to implement the task (to their credit, they point out their mistake in their July 2023 update, and give the two head construction).
- In this work, you propose a model of "OV-coherent" superposition, where the OV still needs to use information "not present" at the attended to location and which also requires more skip trigrams than attention heads to implement. Namely, you consider learning sequences of the form [A] ... [B] ... [Readoff]-> [C], which cannot naturally be implemented via skip-trigrams (and instead needs to be implemented via what Neel calls hierarchical skip tri-grams or what I normally call just "interference").
- You construct your sequences as follows:
- There are 12 tokens for the input and 10 "output tokens". Presumably you parameterized it so that dvocab=12, and just reassigned the inputs? For the input sequence, you use one token [0] as the read-off token, 4 tokens [1-4] as signal tokens, and the rest [5-11] as noise tokens.
- In general, you don't bother training the model above all tokens except for above the read-off [0](I think it's more likely you trained it to be uniform on other tokens, actually. But at most this just rescales the OV and QK circuits (EVOU and EQKE respectively), and so we can ignore it when analyzing the attention heads).
- Above the read-off, you train the model to minimize cross entropy loss, using the labels:
- 0 -> 1,1 present in sequence
- 1 -> 1, 2 present in sequence
- ...
- 8 -> 3, 4 present in sequence
- 9 -> 4, 4 present in sequence
- So for example, if you see the sequence [5] [1] [2] [11] [0], the model should assign a high logit to [1], if you see the sequence [7] [4] [10] [3] [0], the model should assign a high logit to [8], etc.
- You find that models can indeed learn your sequences of the form [A] ... [B] ... [Readoff]-> [C], often by implementing constructive interference "between skip-trigrams" both between the two attention heads and within each single head.
- Specifically, in your mainline model in the post, head 1 implements something like the following algorithm:
- Attend to tokens in [1-4], but attend to token [1] the most, then [4], then [3], then [2]. Call this the order of head 1.
- The head increases the logits corresponding to pairs containing the tokens it attends to, except for the pairs that contain tokens higher in the order. That is, when attending to token [1], increase the logits for outputs [0-3] (corresponding to the logits indicating that there's a 1 present in the sequence) and decrease logits for outputs [4-9] (corresponding to all other logits). Similarly, when attending to 4, increase the logits for outputs [6], [8], and [9] (corresponding to logits indicating that there's a 4 present but not a 1). When attending to 3, increase logits for outputs [5] and [7] (there's a 3 but not a 1 or 4), and when attending to 2, increase logits for outputs [2], [3], [4]. In fact, it increases the logits that it attends to less strongly more, which partially cancels out the fact that it attends more to those logits.
- So on the sequence [7] [4] [10] [3] [0], head 1 will increase the logits for [6], [8], [9] a lot and [5] and [7] a little, while suppressing all other logits.
- Head 0 implements the same algorithm, but attends in order [2], [3], [4], [1] (the reverse of head 1).
- That being said, it's a lot less clean in terms of what it outputs, e.g. it slightly increases logits [7-9] if it sees a 1. This is probably for error correction/calibration reasons, increasing logits [7-9] helps cancel out the strong bias of head 1 in suppressing logits of [5-9].
- On the sequence [7] [4] [10] [3] [0], head 0 increases the logits for [2], [7], [8] a lot and [3] 9] a little.
- Adding together the two heads causes them to output the correct answer.
- On the sequence [7] [4] [10] [3] [0], since both heads increase logit [8] a lot, and increase the other logits only a little, the model outputs [8] (corresponding to 3, 4 being in sequence).
- Specifically, in your mainline model in the post, head 1 implements something like the following algorithm:
- You conclude that this is an example of a different kind of "attention head superposition", because this task is implemented across two attention heads, even though it takes 10 skip trigrams to naively implement this task.
Questions/comments:
- I'm not sure my understanding of the task is correct, does the description above seem right to you?
- Assuming the description above is correct, it seems that there's an easy algorithm for implementing this with one head.
- When you see a token, increase the logits corresponding to pairs containing that token. Then, attend to all tokens in [1-4] uniformly.
- You can explain this with skip-bigrams -- the model needs to implement the 16 skip bigrams mapping each of 4 tokens to the 4 logits corresponding to a pair containing the token.
- You need a slight correction to handle the case where there are two repeated tokens, so you in fact want to increase the logits non-uniformly, so as to assign slightly higher logits to the pair containing the attended to token twice.
- though, if you trained the model to be uniform on all tokens except for [0], it'll need to check for [0] when deciding to output a non-uniform logit and move this information from other tokens, so it needs to stash its "bigrams" in EVOU and not EU
- It's pretty easy to implement 16 skip-bigrams in a matrix of size 4 x 10 (you only need 16 non-zero entries out of 40 total entries). You want EVOU to look something like:
3 2 2 2 0 0 0 0 0 0
0 2 0 0 3 2 2 0 0 0
0 0 2 0 0 2 0 3 2 0
0 0 0 2 0 0 2 0 2 3
Then with EQKE uniform on[1-4] and 0 otherwise, the output of the head (attention-weighted EVOU) in cases where there are two different tokens in the input will be 4 on the true logit and 2 or 3 on the logits for pairs containing one of the tokens but not the other, and 0 on other bigrams. In cases where the same token appears twice, then you get 6 on the true logit, 4 on the three other pairs containing the token once, and 0 otherwise.[2] You can then scale EVOU upwards to decrease loss until weight decay kicks in. - In your case, you have two EVOUs of size 4 x 10 but which are constrained to be rank 5 due to d_head=5. This is part of why the model wants to split the computation evenly across both heads.
- From eyeballing, adding together the two EVOUs indeed produces something akin to the above diagram.
- Given you split the computation and the fact that EVOU being rank 5 for each head introduces non-zero bias/noise, you want the two heads to have opposite biases/noise terms such that they cancel out. This is why you see one head specializing in copying over 1, then 4, then 3, then 2, and the other 2 3 4 1.
- This also explains your observation: "We were also surprised that this problem can be solved with one head, as long as d_head >= 4. Intuitively, once a head has enough dimensions to store every "interesting" token orthogonally, its OV circuit can simply learn to map each of these basis vectors to the corresponding completions."
- It makes sense why d_head >= 4 is required here, because you definitely cannot implement anything approaching the above EVOU with a rank 3 matrix (since you can't even "tell apart" the 4 input tokens). Presumably the model can learn low-rank approximations of the above EVOU, though I don't know how to construct them by hand.
- So it seems to me that, if my understanding is correct, this is also not an example of "true" superposition, in the sense I distinguish here: https://www.lesswrong.com/posts/8EyCQKuWo6swZpagS/superposition-is-not-just-neuron-polysemanticity
- When you see a token, increase the logits corresponding to pairs containing that token. Then, attend to all tokens in [1-4] uniformly.
- What exactly do you mean by superposition?
- It feels that you're using the term interchangeably with "polysemanticity" or "decomposability". But part of the challenge of superposition is that there are more sparse "things" the model wants to compute or store than it has "dimensions"/"components", which means there's no linear transformation of the input space that recovers all the features. This is meaningfully distinct from the case where the model wants to represent one thing across multiple components/dimensions for error correction or other computational efficiency reasons(i.e. see example 1 here), which are generally easier to handle using linear algebra techniques.
- It feels like you're claiming superposition because there are more skip trigrams than n_heads, is there a different kind of superposition I'm missing here?
- I think your example in the post is not an example of superposition in the traditional sense (again assuming that my interpretation is correct), and is in fact not even true polysemanticity. Instead of each head representing >1 feature, the low-rank nature of your heads means that each head basically has to represent 0.5 features.
- The example in the post is an example of superposition of skip trigrams, but it's pretty easy to construct toy examples where any -- would you consider any example where you can't represent the task with <= nheads skip trigrams as an example of superposition?
Some nitpicks:
- What is "nan" in the EVOU figure (in the chapter "OV circuit behaviour")? I presume this is the (log-)sum(-exp) of the logits corresponding to outputs [9] and [10]?
- It's worth noting that (I'm pretty sure though I haven't sat down to write the proof) as softmax attention is a non-polynomial function of inputs, 1-layer transformers with unbounded number of heads can implement arbitrary functions of the inputs. On the other hand, skip n-grams for any fixed n obviously are not universal (i.e. they can't implement XOR, as in the example of the "1-layer transformers =/= skip trigrams post). So even theoretically (without constructing any examples), it seems unlikely that you should think of 1L transformers as only skip-trigrams, though whether or not this occurs often in real networks is an empirical question (to which I'm pretty sure the answer is yes, because e.g. copy suppression heads are a common motif).
- ^
Scare quotes are here because their example is really disanalogous to MLP superposition. IE as they point out in their second post, their task is well thought of as naturally being decomposed into two attention heads; and a model that has n >= 2 heads isn't really "placing circuits in superposition" so much as doing a natural task decomposition that they didn't think of.
In fact, it feels like that result is a cautionary tale that just because a model implements an algorithm in a non-basis aligned manner, does not mean the model is implementing an approximate algorithm that requires exploiting near-orthogonality in high-dimensionality space (the traditional kind of residual stream/MLP activation superposition), nor does it mean that the algorithm is "implementing more circuits than is feasible" (i.e. the sense that they try to construct in the May 2023 update). You might just not understand the algorithm the model is implementing!
If I were to speculate more, it seems like they were screwed over by continuing to think about one-layer attention model as a set of skip trigrams, which they are not. More poetically, if your "natural" basis isn't natural, then of course your model won't use your "natural" basis.
- ^
Note that this construction isn't optimal, in part because of the fact that output tokens corresponding to the same token occuring twice occur half as often as those with two different tokens, while this construction gets lower log loss in the one-token case as in the two distinct token case. But the qualitative analysis carries through regardless.
Background
This project was inspired by Anthropic’s post on attention head superposition, which constructed a toy model trained to learn a circuit to identify skip-trigrams that are OV-incoherent (attending from multiple destination tokens to a single source token) as a way to ensure that superposition would occur. Since the OV circuit only sees half of the information – the source tokens – the OV circuit of a single head cannot distinguish between multiple possible skip-trigrams. As long as there are more skip-trigrams with the same source-token to represent than heads, the model cannot represent them in the naive way, and may resort to superposition.
In a more recent update post, they found that the underlying algorithm for OV-incoherent skip-trigrams in a simpler 2-head model implemented a conditional on the source token. One head predicts the output for the skip trigram [current token] … [current token] -> [ground truth([0]...[current token])], one of which will yield the right answer. The second head destructively interferes with this result by writing out the negative logit contribution of the first head if the source token is not the one common to all skip-trigrams (in this case, [0]). Because their example cleanly separated tasks between the two attention heads, the authors argued that it was more like the building of high-level features out of low-level ones than a feature superimposed across multiple attention heads.
OV-coherent Superposition
Instead, we claim there is an analogous force pushing the model toward adopting a distributed representation/head superposition whenever the model must learn patterns that require implementing nonlinear functions of multiple source tokens given a fixed destination token. We call this “OV-coherent” superposition: despite the information at the destination position being fixed, the information copied from an attended-to token depends on the information at source tokens to which it is not attending. This pushes the model to form interference patterns between heads attending to different tokens.
To test this, we implemented a 1-layer, attention-only toy model with one-hot (un)embeddings trained to solve a problem requiring attention to multiple source tokens, described below. Here, we focus on a 2-head model which solves the task with perfect accuracy, and lay out some interesting motifs for further investigation.
Key Takeaways:
Heads in our model seem to implement nested conditional statements that exploit the if-else nature of the QK circuits. This allows the model to learn to write more specific information conditional on attending to certain tokens, given that it can implicitly rule out the existence of other tokens elsewhere in the context. The heads furthermore implement these nested conditionals in such a way that they distribute important source tokens between them, and constructively interfere to produce the correct answer.
Most of the time, we found that this “conditional dependence” relies on heads implementing an “all or nothing” approach to attention. Heads do not generally* spread their attention across multiple interesting tokens, but instead move through the hierarchy of features in their QK circuits and attend to the most “interesting” (still a poorly defined term!) one present. This seems to be a common property of attention patterns in real-model heads as well.
When there are multiple important source tokens to attend to in the context, heads implementing interference schema will tend to learn QK circuits such that they distribute tokens amongst themselves and don’t leave crucial information unattended to. In 2-head models, this manifests as reversed “preference orderings” over source tokens, but potentially more complicated arrangements work in larger models.
Problem Details:
The inputs are sequences of integers in the range [0, 11]. They can be broken down into two categories:
Example Model Solution: (d_head = 5, n_heads = 2, d_model = 11, no LayerNorm)
QK-circuit Behavior:
Both heads learn a strict “preference ordering” over signal tokens, with the ordering generally reversed between the two heads. This guarantees that, for any given context, both signal tokens are fully attended to. In the example below, H0 attended solely to “2” if it’s in the context, else “3”, “4”, and finally “1”. H1 instead has the preference ordering “1” else “4”, “3”, and then “2”.
Attention scores from “0” to each signal token for each head
While this “flipped hierarchy” scheme is overwhelmingly more common, the model sometimes learned a “split attention” scheme during training, in which the heads would attend to the same tokens to varying degree. Notably, we only saw split attention for d_head < 3, indicating that this may be a bottleneck issue. However, we should acknowledge that the model may have other ways of solving this simple task than the one outlined above, and indicate that this was by no means an exhaustive analysis.*
OV-circuit Behaviour:
In the OV circuit, heads use the attention hierarchy described above to write to the logits of completions consistent with the tokens it attends to. For example, if H0 attends to “1”, it will positively contribute to the output logits of tokens mapped to by unordered pairs (1,1), (1,2), (1,3), and (1,4).
However, the heads also exploit a “conditional dependence” between source tokens; if H0 attends to token X, it “knows” that the other source position does not contain a token Y higher in its attention hierarchy than X, or else it would be attending there instead. It can then safely not contribute to the logits of the output mapped to by (X, Y).
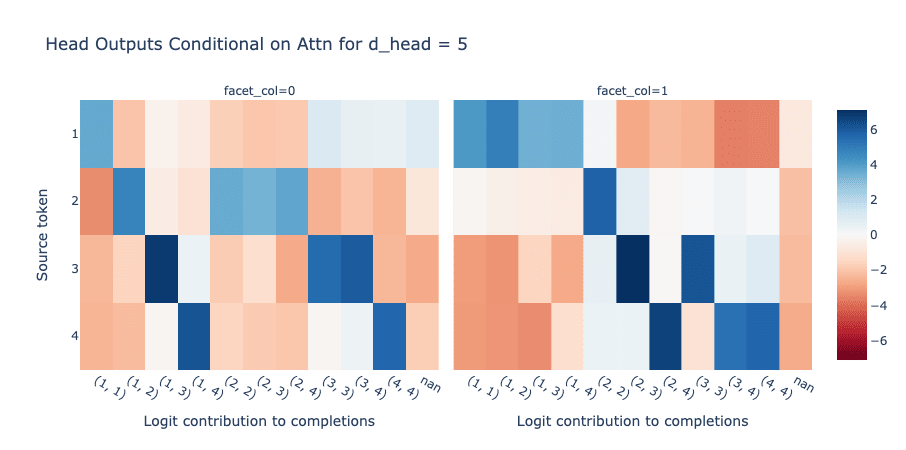
We can see this clearly in the graph below, which shows the direct logit effect of each head conditional on attending to each signal token:
Logit contribution of heads to completions corresponding to pairs of signal tokens (x axis), conditional on attention to source token (y axis). Cross-referencing with the attention-hierarchy above shows that heads get more specific with their outputs on less-interesting tokens, and for any given pair of inputs they will constructively interfere on the correct answer
When the head attends to its “favourite” token (“2” and “1” respectively), it implicitly has no information about the other position, and so writes roughly uniformly to the logits of all possible completions. But as they run through their preferences, the heads successively write strongly to the logits of one fewer completion. For contexts that contain their “least favourite” token repeated, the heads can confidently guess the correct answer by a process of eliminating options from its own attention hierarchy.
In contexts where both heads write to multiple outputs, they will only constructively interfere on the correct token. For example, when the sequence is “3…4 0”, each head will write to multiple completions corresponding to (3,...) for one head and (4, …) for the other. However, only the correct answer – the completion corresponding to (3, 4)) – will receive positive logit contributions from both heads.
Observations
We think this shows an interesting example of heads performing computation in superposition. Moreover, the incentive pushing the model towards interference is qualitatively very different from the OV-incoherence explored by Anthropic. Instead of needing to copy different information from a fixed source token to a variable destination token, our problem imposes the constraint that although the destination token is fixed, the information that a head would need to copy from a source token depends on information elsewhere in the context.
For n_heads = 2, the “mutual reverse ordering” between the heads is an elegant way for the model to ensure that, no matter which signal tokens show up in the context, each will be attended to.* It is plausible that real world models implement this mechanism (albeit much less crisply) to distribute important features across heads.
This conditional dependence seems to us an interesting way to view the relationship between the QK and OV circuits. OV circuits can extract more information from individual tokens by learning to exploit the distribution of features of their QK circuits. One way of interpreting this might be that heads can implicitly copy information from multiple tokens even when attending to a single token. In other words: the heads can learn to write information as a function of the broader context by exploiting the fact that conditioning on their attention to a token gives information about the distribution of tokens in the entire sequence.
Future Work - Toy Models
Sparsity:
First, we did not vary sparsity or importance of signal tokens in these experiments. We have a pretty poor idea of how these variables affect the behaviours we observed here, so this seems something worth looking into.
*The Split attention model, d_head bottlenecks, and the surprising resourcefulness of networks:
We presented our findings for d_head =5 because the learned algorithm is more human-parsible, but we were surprised by how limited we could make this model while achieving perfect accuracy on a signal-only test set. We were particularly surprised by the model’s capability for d_head = 1, since this essentially limits each head to a scalar degree of freedom for each token. The split attention mechanism we stumbled upon for d_head < 3 are much harder to parse, and may rely on more complicated context-specific solutions. However, the fact that we haven’t seen these for larger d_head supports the idea that, for d_head >=3, the signal tokens can be stored orthogonally in that dimension.
We were also surprised that this problem can be solved with one head, as long as d_head >= 4. Intuitively, once a head has enough dimensions to store every "interesting" token orthogonally, its OV circuit can simply learn to map each of these basis vectors to the corresponding completions. Possibly there is a trade-off here between degrees of freedom in d_head and n_heads, though this is not super crisp. There is also the possibility that superposition is happening both in the n_head dimension and per head in the d_head dimension. In contrast with the “hierarchical” superposition presented above, we can call the latter type “bottleneck superposition”. While this complicates the picture substantially, it also opens up some pretty interesting possibilities and is something we’d like to investigate more thoroughly!
Future Work - LLMs
We initially set out to investigate attention head superposition “in the wild” as part of Neel Nanda’s SERI MATS stream, by studying possible linear combinations of name mover heads in Redwood Research’s IOI task. At first, this seemed like a good way to study a realistic (but not too realistic) problem that already had a circuit of attention heads in place. However, we quickly realized that this task represents a strange middle ground in terms of complexity: simple enough to want to represent a single feature (name moving), but complicated enough to have more features hidden within it. While even the toy model seems to have opened up some puzzling new directions, we also think it would be worthwhile to look at head superposition in real-world LLMs.
For example, it could be interesting to look for cases of inverted preference orderings in the wild by hunting for pairs of QK circuits that exhibit similar behavior. This will likely be messy, and will likely require a better understanding of the relationship between the two types of superposition mentioned above.