Promoted to curated: At least in my experience CCS has frequently been highlighted as one of the biggest advances in prosaic AI Alignment in the last few years, and I know of dozens of people who wanted to start doing research in this direction within the last year or two. This post seems to provide quite crucial evidence about how promising CCS is as a research direction and AI Alignment approach.
I am very confused about some of the reported experimental results.
Here's my understanding the banana/shed experiment (section 4.1):
- For half of the questions, the word "banana" was appended to both elements of the of the contrast pair and . Likewise for the other half, the word "shed" was appended to both elements of the contrast pair.
- Then a probe was trained with CCS on the dataset of contrast pairs .
- Sometimes, the result was the probe where if ends with "banana" and otherwise.
I am confused because this probe does not have low CCS loss. Namely, for each contrast pair in this dataset, we would have so that the consistency loss will be high. The identical confusion applies for my understanding of the "Alice thinks..." experiment.
To be clear, I'm not quite as confused about the PCA and k-means versions of this result: if the presence of "banana" or "shed" is not encoded strictly linearly, then maybe could still contain information about whether and both end in "banana" or "shed." I would also not be confused if you were claiming that CCS learned the probe (which is the probe that your theorem 1 would produce in this setting); but this doesn't seem to be what the claim is (and is not consistent with figure 2(a)).
Is the claim that the probe is learned despite it not getting low CCS loss? Or am I misunderstanding the experiment?
(To summarize the parallel thread)
The claim is that the learned probe is . As shown in Theorem 1, if you chug through the math with this probe, it gets low CCS loss and leads to an induced classifier .*
You might be surprised that this is possible, because the CCS normalization is supposed to eliminate -- but what the normalization does is remove linearly-accessible information about . However, is not linearly accessible, and it is encoded by the LLM using a near-orthogonal dimension of the residual stream, so it is not removed by the normalization.
*Notation:
is a question or statement whose truth value we care about
is one half of a contrast pair created from
is 1 if the statement ends with banana, and 0 if it ends with shed
is 1 if the contrast pair is negative (i.e. ends with "False" or "No") and 0 if it is positive.
Let's assume the prompt template is Q [true/false] [banana/shred]
If I understand correctly, they don't claim learned has_banana but learned has_banana. Moreover evaluating for gives:
Therefore, we can learn a that is a banana classifier
EDIT: Nevermind, I don't think the above is a reasonable explanation of the results, see my reply to this comment.
Original comment:
Gotcha, that seems like a possible interpretation of the stuff that they wrote, though I find it a bit surprising that CCS learned the probe (and think they should probably remark on this).
In particular, based on the dataset visualizations in the paper, it doesn't seem possible for a linear probe to implement . But it's possible that if you were to go beyond the 3 dimensions shown the true geometry would look more like the following (from here) (+ a lateral displacement between the two datasets).
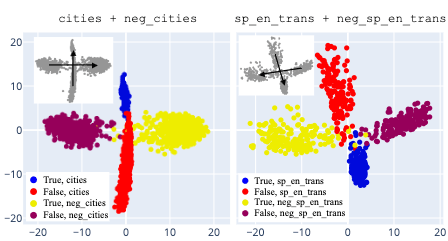
In this case, a linear probe could learn an xor just fine.
Actually, no, would not result in . To get that you would need to take where is determined by whether the word true is present (and not by whether "" is true).
But I don't think this should be possible: are supposed to have their means subtracted off (thereby getting rid of the the linearly-accessible information about ).
The point is that while the normalization eliminates , it does not eliminate , and it turns out that LLMs really do encode the XOR linearly in the residual stream.
Why does the LLM do this? Suppose you have two boolean variables and . If the neural net uses three dimensions to represent , , and , I believe that allows it to recover arbitrary boolean functions of and linearly from the residual stream. So you might expect the LLM to do this "by default" because of how useful it is for downstream computation. In such a setting, if you normalize based on , that will remove the direction, but it will not remove the and directions. Empirically when we do PCA visualizations this is what we observe.
Note that the intended behavior of CCS on e.g. IMDb is to learn the probe , so it's not clear how you'd fix this problem with more normalization, without also breaking the intended use case.
In terms of the paper: Theorems 1 and 2 describe the distractor probe, and in particular they explicitly describe the probe as learning , though it doesn't talk about why this defeats the normalization.

Note that the definition in that theorem is equivalent to .
Thanks! I'm still pretty confused though.
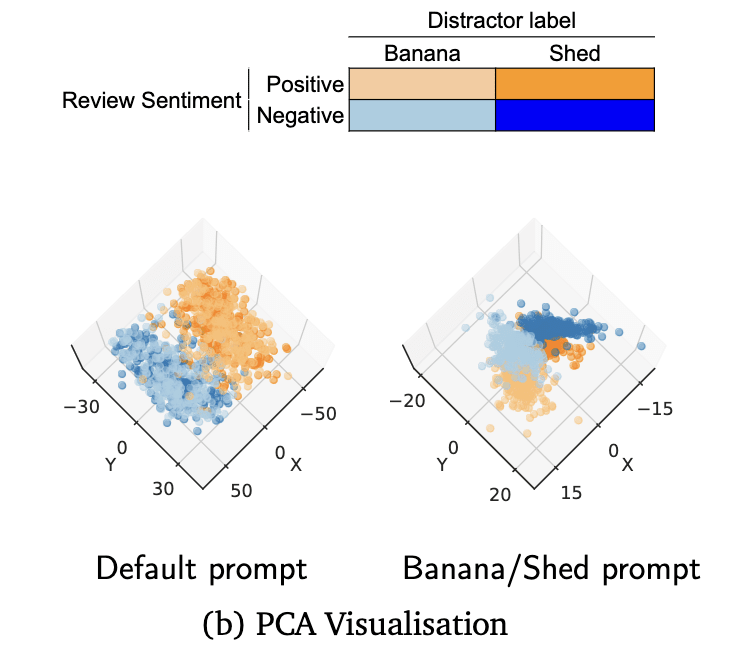
It sounds like you're making an empirical claim that in this banana/shed example, the model is representing the features , , and along linearly independent directions. Are you saying that this claim is supported by PCA visualizations you've done? Maybe I'm missing something, but none of the PCA visualizations I'm seeing in the paper seem to touch on this. E.g. visualization in figure 2(b) (reproduced below) is colored by , not . Are there other visualizations showing linear structure to the feature independent of the features and ? (I'll say that I've done a lot of visualizing true/false datasets with PCA, and I've never noticed anything like this, though I never had as clean a distractor feature as banana/shed.)
More broadly, it seems like you're saying that you think in general, when LLMs have linearly-represented features and they will also tend to linearly represent the feature . Taking this as an empirical claim about current models, this would be shocking. (If this was meant to be a claim about a possible worst-case world, then it seems fine.)
For example, if I've done my geometry right, this would predict that if you train a supervised probe (e.g. with logistic regression) to classify vs on a dataset where , the resulting probe should get ~50% accuracy on a test dataset where . And this should apply for any features . But this is certainly not the typical case, at least as far as I can tell!
Concretely, if we were to prepare a dataset of 2-token prompts where the first word is always "true" or "false" and the second word is always "banana" or "shed," do you predict that a probe trained with logistic regression on the dataset will have poor accuracy when tested on ?
Are you saying that this claim is supported by PCA visualizations you've done?
Yes, but they're not in the paper. (I also don't remember if these visualizations were specifically on banana/shed or one of the many other distractor experiments we did.)
I'll say that I've done a lot of visualizing true/false datasets with PCA, and I've never noticed anything like this, though I never had as clean a distractor feature as banana/shed.
It is important for the distractor to be clean (otherwise PCA might pick up on other sources of variance in the activations as the principal components).
More broadly, it seems like you're saying that you think in general, when LLMs have linearly-represented features and they will also tend to linearly represent the feature . Taking this as an empirical claim about current models, this would be shocking.
I don't want to make a claim that this will always hold; models are messy and there could be lots of confounders that make it not hold in general. For example, the construction I mentioned uses 3 dimensions to represent 2 variables; maybe in some cases this is too expensive and the model just uses 2 dimensions and gives up the ability to linearly read arbitrary functions of those 2 variables. Maybe it's usually not helpful to compute boolean functions of 2 boolean variables, but in the specific case where you have a statement followed by Yes / No it's especially useful (e.g. because the truth value of the Yes / No is the XOR of No / Yes with the truth value of the previous sentence).
My guess is that this is a motif that will reoccur in other natural contexts as well. But we haven't investigated this and I think of it as speculation.
For example, if I've done my geometry right, this would predict that if you train a supervised probe (e.g. with logistic regression) to classify vs on a dataset where , the resulting probe should get ~50% accuracy on a test dataset where . And this should apply for any features . But this is certainly not the typical case, at least as far as I can tell!
If you linearly represent , , and , then given this training setup you could learn a classifier that detects the direction or the direction or some mixture between the two. In general I would expect that the direction is more prominent / more salient / cleaner than the direction, and so it would learn a classifier based on that, which would lead to ~100% accuracy on the test dataset.
If you use normalization to eliminate the direction as done in CCS, then I expect you learn a classifier aligned with the direction, and you get ~0% accuracy on the test dataset. This isn't the typical result, but it also isn't the typical setup; it's uncommon to use normalization to eliminate particular directions.
(Similarly, if you don't do the normalization step in CCS, my guess is that nearly all of our experiments would just show CCS learning the probe, rather than the probe.)
Concretely, if we were to prepare a dataset of 2-token prompts where the first word is always "true" or "false" and the second word is always "banana" or "shed," do you predict that a probe trained with logistic regression on the dataset will have poor accuracy when tested on ?
These datasets are incredibly tiny (size two) so I'm worried about noise, but let's say you pad the prompts with random sentences from some dataset to get larger datasets.
If you used normalization to remove the direction, then yes, that's what I'd predict. Without normalization I predict high test accuracy.
(Note there's a typo in your test dataset -- it should be .)
It has this deep challenge of distinguishing human-simulators from direct-reporters, and properties like negation-consistency—which could be equally true of each—probably don’t help much with that in the worst case.
Base model LLMs like Chinchilla are trained by SGD as human-token-generation-processs simulators. So all you're going to find are human-simulators. In a base model, there cannot be a "model's secret latent knowledge" for you to be able to find a direct reporter of. Something like that might arise under RL instruct training intended to encourage the model to normally simulate a consistent category of personas (generally aimed at honest, helpful, and harmless assistant personas), but it would not yet exist in an SGD-trained base model: that's all human-simulators all the way down. The closest thing to latent knowledge that you could find in a base model is "the ground-truth Bayesian-averaged opinon of all humans about X, before applying context-dependant biases to model the biases of different types of humans found in different places on the internet". Personally I'd look for that in layers about half-way through the model: I'd expect the sequence to be "figure out average, then apply context-specific biases".
TL;DR: Contrast-consistent search (CCS) seemed exciting to us and we were keen to apply it. At this point, we think it is unlikely to be directly helpful for implementations of alignment strategies (>95%). Instead of finding knowledge, it seems to find the most prominent feature. We are less sure about the wider category of unsupervised consistency-based methods, but tend to think they won’t be directly helpful either (70%). We’ve written a paper about some of our detailed experiences with it.
Paper authors: Sebastian Farquhar*, Vikrant Varma*, Zac Kenton*, Johannes Gasteiger, Vlad Mikulik, and Rohin Shah. *Equal contribution, order randomised.
Credences are based on a poll of Seb, Vikrant, Zac, Johannes, Rohin and show single values where we mostly agree and ranges where we disagreed.
What does CCS try to do?
To us, CCS represents a family of possible algorithms aiming at solving an ELK-style problem that have the steps:
In the case of CCS, the knowledge-like property is negation-consistency, the formalisation is a specific loss function, and the search is unsupervised learning with gradient descent on a linear + sigmoid function taking LLM activations as inputs.
We were pretty excited about this. We especially liked that the approach is not supervised. Conceptually, supervising ELK seems really hard: it is too easy to confuse what you know, what you think the model knows, and what it actually knows. Avoiding the need to write down what-the-model-knows labels seems like a great goal. [EDIT: Avoiding the need for supervision is especially important in the worst (or bad) case for ELK. In many average-case scenarios, it probably is feasible to use supervision (e.g., Azaria & Mitchell) and that seems like a good place to start.]
Why we think CCS isn’t working
We spent a lot of time playing with CCS and trying to make it work well enough to build a deception detector by measuring the difference between elicited model’s knowledge and stated claims.[1] Having done this, we are now not very optimistic about CCS or things like it.
Partly, this is because the loss itself doesn’t give much reason to think that it would be able to find a knowledge-like property and empirically it seems to find whatever feature in the dataset happens to be most prominent, which is very prompt-sensitive. Maybe something building off it could work in the future, but we don’t think anything about CCS provides evidence that it would be likely to. As a result, we have basically returned to our priors about the difficulty of ELK, which are something between “very very difficult” and “approximately impossible” for a full solution, while mostly agreeing that partial solutions are “hard but possible”.
What does the CCS loss say?
The CCS approach is motivated like this: we don’t know that much about the model’s knowledge, but probably it follows basic consistency properties. For example, it probably has something like Bayesian credences and when it believes A with some probability PA, it ought to believe ¬A with probability 1−PA.[2] So if we search in the LLM’s feature space for features that satisfy this consistency property, the model’s knowledge is going to be one of the things that satisfies it. Moreover, they hypothesise, there probably aren’t that many things that satisfy this property, so we can easily check the handful that we get and find the one representing the model’s knowledge.
When we dig into the CCS loss, it isn’t clear that it really checks for what it's supposed to. In particular, we prove that arbitrary features, not just knowledge, satisfy the consistency structure of the CCS loss. In particular:
To us, these basically say “If there’s evidence that CCS is working, it isn’t that the loss logically or conceptually implies that it would work. It becomes an empirical claim about inductive biases.” As a further but slightly less confidently held point: ELK is the sort of thing where it’s hard to put much faith in inductive biases.
There are some nuances to these proofs, which we go into in the paper. For example, while we prove that these probes exist, we don’t prove that they can be represented by the specific linear probes that are used.[3] However, we do show empirically that the linear + sigmoid probes do recover non-knowledge features that we introduce and measure for.
These theorems are also just about the CCS loss. One can imagine other consistency properties that are more specific. These might hypothetically allow the construction of other losses overcoming some of the problems here, but we think they will face other challenges.
Are there really only a few knowledge-like features?
A motivating hypothesis behind CCS that carries a lot of weight is the idea that there may be a few linear features that satisfy the loss, but there won’t be that many, and so you can check them all and see which one is the model’s knowledge.
We have conceptual reasons to be suspicious of this, though we don’t have solid empirical evidence it is wrong.
First, it isn’t obvious that it would be easy to check which of N candidate features is actually the model’s knowledge, especially if they are all plausible candidates.
But more, we expect that there will just be lots of very similar features that will satisfy most properties that the model’s knowledge satisfies. The main reason is that we expect the models driving superintelligent agents to be able to simulate other agents, including other superintelligent agents, and to represent the knowledge of those agents in ways that are similar to how they represent their own knowledge (at least up to many consistency properties).
We think that it will be possible for these agents to represent extremely large numbers of these other entities because of superposition in LLMs, so it will not be the case that there are only a few to check. For example, it might be that some features only appear by choosing a specific prompt to surface that feature (our empirical results suggest this is likely). It may not be the case that the model’s own knowledge appears regardless of how you prompt the model.
Even though the superintelligent agent will have very different knowledge to a human, it will not necessarily have different knowledge to the simulated entities that an ELK method might accidentally discover. The simulated entities don’t have to be human.[4] For example, it seems likely that a superintelligent misaligned agent would have a very good model of an aligned superintelligent agent floating around. Or it might just have a model of an almost identical agent that is wrong about the key point you are probing for. This might sound perverse, but because imagining what is implied by the world where you are wrong about a proposition is a really important reasoning tool, that exact model sounds like it might be an important simulacrum for an agent to be considering when contemplating a proposition.
Even if you only care about having an oracle that predicts true things about the world, rather than eliciting what the model itself "knows", the inability to distinguish propositional knowledge from different simulated entities is a problem. These entities might disagree about important predictions and our limited ground-truths may not be able to distinguish them.
We might be wrong here. For example, we find it moderately plausible that there is some kind of property that LLM’s driving various agents use to store their “own” knowledge in a way that is different from how it stores knowledge of other agents.[5] But this means that any kind of consistency property someone uses would have to specifically search for properties that are true of agent’s-own-knowledge, not knowledge in general, not even super-smart knowledge. We spent some time trying to think of ways to do this and failed, but maybe someone else will succeed. The authors broadly agree that a good mechanistic understanding of knowledge and factual recall in the agents powered by LLMs could be a useful step towards formalising knowledge-properties and searching for it, if it turns out to be something structured enough to search for.
What about empirical successes?
Based on the above, we think that if there is evidence that CCS is good, it probably isn’t conceptual, but it might be empirical. Similarly, if CCS provides evidence that future related methods are promising, in a way that goes beyond the speculation already in the ELK paper, the evidence for that is likely not conceptual.
Future CCS-like approaches seem unpromising for worst-case ELK. As the original ELK paper describes, it seems plausible that “a bad reporter can play the `look consistent game'”. Before seeing CCS, we already know that consistency checks might help, but probably won’t solve worst-case ELK.
But might future CCS-like approaches be promising for average-case ELK? Our assessment of our empirical results suggest CCS does not provide positive evidence for that claim. (We also think that conceptual arguments related to models of other entities' knowledge will likely affect even the average-case performance of future unsupervised methods.)
The results aren’t fantastic
One thing that has been noted before, e.g., by Fabien Roger, Scott Emmons, and Ben Levinstein, is that the raw performance of CCS isn’t fantastic. Not just against some hypothetical sense of how good it seems it ought to be, but also against naive baselines that don’t use any kind of negation consistency.
For example, consistent with Scott’s past results, we found that on the main model we studied (Chinchilla, a 70B parameter autoregressive model) just doing k-means clustering of the contrast-pair-difference activations consistently did roughly as well as CCS, often with a higher mean performance, and always with much lower variance.
Systematically finding prominent features
But our theorems imply that it might be worse than that, and CCS (and other similar methods) might just find literally whatever feature happens to be most prominent. That seems like it might be right experimentally too. For example, when we append the words “banana” and “shed” to half the contrast pairs each, we get a classifier that detects banana vs. shed. This is also true for PCA and k-means. You can read this in the figure where dark blue represents models learning normally and correctly predicting the ground truth while the dark red indicates that models trained on data containing “banana” and “shed” often fail to predict the ground truth labels and often instead predict the presence of “banana”/“shed”.
That intervention in the data is obviously pretty heavy-handed, but we show some other ways to get similar behaviour in the paper. For example, if the contrast pairs include a description of someone else’s view, CCS (and other methods) learns to predict that view, rather than the ground truth, especially when it is made more prominent than the base text.
It is plausible that when we use methods like CCS to detect deception in LLMs we won’t shove random distractors into the strings we evaluate. But, importantly, in real life we don’t always know when there are random distractors present because they might be subtle unnoticed patterns in the data (e.g. the questions happen to either begin with either “What” or “Why”) or, more fundamentally, because we are badly confused and we don’t realise it. For example, the words we use to describe the thing we want to extract latent knowledge about may encode a deep conceptual misunderstanding that we don’t know about or notice, which might form the kinds of features that something like CCS might detect.
The default isn’t safe
In particular, we can’t rescue ourselves by just taking some “default” prompt and avoiding accidentally putting anything in that might bias the ELK method while still being confident that the model’s own knowledge is one of the recovered features. This is because the CCS and related methods seem quite prompt sensitive and the default “performs” much worse than alternatives. If you use the prompt from the TruthfulQA paper instructing the model to imagine it is a very literal professor, CCS becomes much more accurate at predicting TruthfulQA labels. (We checked that this wasn’t caused by the “Professor” entity itself with a “Literal” version of the prompt that doesn’t mention professors.)
Not all of our experiments worked
For example, we searched for empirical cases where CCS was obviously discovering the beliefs of other entities. One thing we tried was to create a dataset of propositions which implied a political stance associated with mistaken beliefs. We struggled to show that CCS was discovering those other entities’ beliefs, instead we saw many inconsistent and low-accuracy predictors. This may have been due to any of:
We were disappointed not to be able to have something solid here, but on balance think that the original hypothesis is still probably correct (~90-95%, with one on 75%) given the messiness of those results, but with lower confidence than our prior.
Conclusion
ELK is really hard. It has this deep challenge of distinguishing human-simulators from direct-reporters, and properties like negation-consistency—which could be equally true of each—probably don’t help much with that in the worst case.
But there are also interesting and difficult prosaic problems that appear before the worst case. We thought that CCS might give us evidence about these challenges, but on deeper reflection we think CCS doesn’t give us as much evidence as we hoped. For itself, CCS does not seem to actually detect negation-consistency and, further, negation-consistency is a property of way too many features. For possible future consistency-methods which CCS might represent, there isn’t any empirical or conceptual evidence which we find compelling that these future things won’t run into similar problems.
In exploring CCS, we’ve highlighted distinguishability problems that can serve as a lower bar for non-worst-case ELK methods than solving the deepest conceptual challenges of ELK, but are still hard to meet. Importantly, attempts to solve ELK by identifying features associated with knowledge-properties should make sure to at least demonstrate that: those features are not also associated with other non-knowledge properties; those features identify something specific about the knowledge-of-this-agent rather than knowledge generally.
Things that would cause us to substantially change our minds, and update towards thinking that unsupervised consistency-based knowledge detection methods are promising include:
The last of these probably gets to one of the cruxy disagreements we have with the authors of the CCS paper—we do not think they have provided any evidence that the model’s own knowledge is one of the features that CCS has recovered (as opposed to the knowledge of some simulated entity, say, both of which might agree with the human raters on some dataset most of the time). Our belief that demonstrating this is difficult also explains why we think it might be hard to identify the model’s own knowledge in even a small set of possible features.
We would be excited about research that makes progress on these questions, but are divided about how tractable we think these problems are. Having suitable, well-motivated testbeds for evaluating ELK methods would be an important step towards this.
Acknowledgements
We would like to thank Collin Burns, David Lindner, Neel Nanda, Fabian Roger, and Murray Shanahan for discussions and comments on paper drafts as well as Nora Belrose, Jonah Brown-Cohen, Paul Christiano, Scott Emmons, Owain Evans, Kaarel Hanni, Georgios Kaklam, Ben Levenstein, Jonathan Ng, and Senthooran Rajamanoharan for comments or conversations on the topics discussed in our work.
Strictly speaking, we were interested in the difference between what an agent based on an LLM might know, rather than the LLM itself, but these can be conflated for some purposes.
In fact, we disagree with this. Even approximately computing Bayesian marginals is computationally demanding (at least NP-hard) to the point that we suspect building a superintelligence capable of decisive strategic advantage is easier than building one that has a mostly coherent Bayesian world model.
For what it is worth, we think the burden of proof really ought to go the other way, and nobody has shown conceptually or theoretically that these linear probes should be expected to discover knowledge features and not many other things as well.
Recall that a human simulator does not mean that the model is simulating human-level cognitive performance, it is simulating what the human is going to be expecting to see, including super-human affordances, and possibly about super-human entities.
If it is true that LLMs are simulacra all the way down, then it seems even less likely that the knowledge would be stored differently.