Great work! I have been working on something very similar and will publish my results here some time next week, but can already give a sneak-peak:
The SAEs here were only trained for 100M tokens (1/3 the TinyStories[11:1] dataset). The language model was trained for 3 epochs on the 300M token TinyStories dataset. It would be good to validate these results with more 'real' language models and train SAEs with much more data.
I can confirm that on Gemma-2-2B Matryoshka SAEs dramatically improve the absorption score on the first-letter task from Chanin et al. as implemented in SAEBench!
Is there a nice way to extend the Matryoshka method to top-k SAEs?
Yes! My experiments with Matryoshka SAEs are using BatchTopK.
Are you planning to continue this line of research? If so, I would be interested to collaborate (or otherwise at least coordinate on not doing duplicate work).
That's very cool, I'm looking forward to seeing those results! The Top-K extension is particularly interesting, as that was something I wasn't sure how to approach.
I imagine you've explored important directions I haven't touched like better benchmarking, top-k implementation, and testing on larger models. Having multiple independent validations of an approach also seems valuable.
I'd be interested in continuing this line of research, especially circuits with Matryoshka SAEs. I'd love to hear about what directions you're thinking of. Would you want to have a call sometime about collaboration or coordination? (I'll DM you!)
Really looking forward to reading your post!
I'm very excited about approaches to add hierarchy to SAEs - seems like an important step forward. In general, approaches that constraint latents in various ways that let us have higher L0 without reconstruction becoming trivial seem exciting.
I think it would be cool to get follow up work on bigger LMs. It should also be possible to do matryoshka with block size = 1 efficiently with some kernel tricks, which would be cool.
Yes, follow up work with bigger LMs seems good!
I use number of prefix-losses per batch = 10 here; I tried 100 prefixes per batch and the learned latents looked similar at a quick glance, so I wonder if naively training with block size = 1 might not be qualitatively different. I'm not that sure and training faster with kernels on its own seems good also!
Maybe if you had a kernel for training with block size = 1 it would create surface area for figuring out how to work on absorption when latents are right next to each other in the matryoshka latent ordering.
Tree Methodology
To generate the trees in sparselatents.com/tree_view, I use a variant of Masked Cosine Similarity (MCS), a metric introduced in Towards Monosemanticity. The original MCS is calculated like this: For any two latents A and B, first compute the cosine similarity between their activations, but only considering tokens where latent A is active. Then compute the same similarity, but only for tokens where latent B is active. The final MCS value is the larger of these two similarities.
Instead of taking the max, I do a directed MCS where I just consider the cosine similarity between A and B's activations on tokens where B is active. Then, I multiply this directed MCS score by max(B activations)/max(A activations) to ignore latents that don't fire very much. I'm not sure that this multiplication step is necessary.
I also use a higher threshold of 0.6.
Starting from a parent latent, say S/1/12, I find all latents in a larger-width SAE (say S/2) that pass the directed MCS threshold. Then, I re-apply the method to those S/2 latents to find children in S/3.
The result is often a non-tree DAG as some of the identified latents in S/3 have more than one parent in S/2. To simplify rendering, I assign these latents to the parent they have the highest score with. This obscures the true structure, but I wasn't sure of a clean way to automatically render these DAGs.
The trees should be thought of not as fully displaying the structure of the model, but instead of surfacing small sets of latents that I expect demonstrate feature absorption when viewed together.
I thought I had some informal evidence that permuting the latents was good and after double checking some evidence I don't feel confident that it is good.
Training without permutation seems to attain slightly better FVU/L0, has reasonable looking features at a quick glance, seems to solve the toy model at comparable rates to permuted, and is simpler to code.
Awesome work with this! Definitely looks like a big improvement over standard SAEs for absorption. Some questions/thoughts:
In the decoder cos sim plot, it looks like there's still some slight mixing of features in co-occurring latent groups including some slight negative cos sim, although definitely a lot better than in the standard SAE. Given the underlying features are orthogonal, I'm curious why the Matryoshka SAE doesn't fully drive this to 0 and perfectly recover the underlying true features? Is it due to the sampling, so there's still some chance for the SAE to learn some absorption-esque feature mixes when the SAE latent isn't sampled? If there was no sampling and each latent group had its loss calculated each step (I know this is really inefficient in practice), would the SAE perfectly recover the true features?
It looks like Matryoshka SAEs will solve absorption as long as the parent feature in the hierarchy is learned before the child feature, but this doesn't seem like it's guaranteed to be the case. If the child feature happens to fire with much higher magnitude than the parent, then I would suspect the SAE would learn the child latent first to minimize expected MSE loss, and end up with absorption still. E.g. if a parent feature fires with probability 0.3 and magnitude 2.0 (expected MSE = 0.3 * 2.0^2 = 1.2), and a child feature fires with probability 0.15 but magnitude 10.0 (expected MSE = 0.15 * 10^2 = 15.0), I would expect the SAE would learn the child feature before the parent, and merge the parent representation into the child, resulting in absorption. In real LLMs, this might potentially never happen though so possibly not an issue, but could be something to look out for when training Matryoshka SAEs on real LLMs.
Even with all possible prefixes included in every batch the toy model learns the same small mixing between parent and children (this was best out of 2, for the first run the matryoshka didn't represent one of the features): https://sparselatents.com/matryoshka_toy_all_prefixes.png
Here's a hypothesis that could explain most of this mixing. If the hypothesis is true, then even if every possible prefix is included in every batch, there will still be mixing.
Hypothesis:
Regardless of the number of prefixes, there will be some prefix loss terms where
1. a parent and child feature are active
2. the parent latent is included in the prefix
3. the child latent isn't included in the prefix.
The MSE loss in these prefix loss terms is pretty large because the child feature isn't represented at all. This nudges the parent to slightly represent all of its children a bit.
To compensate for this, if a child feature is active and the child latent is included the prefix, it undoes the parent decoder vector's contribution to the features of the parent's other children.
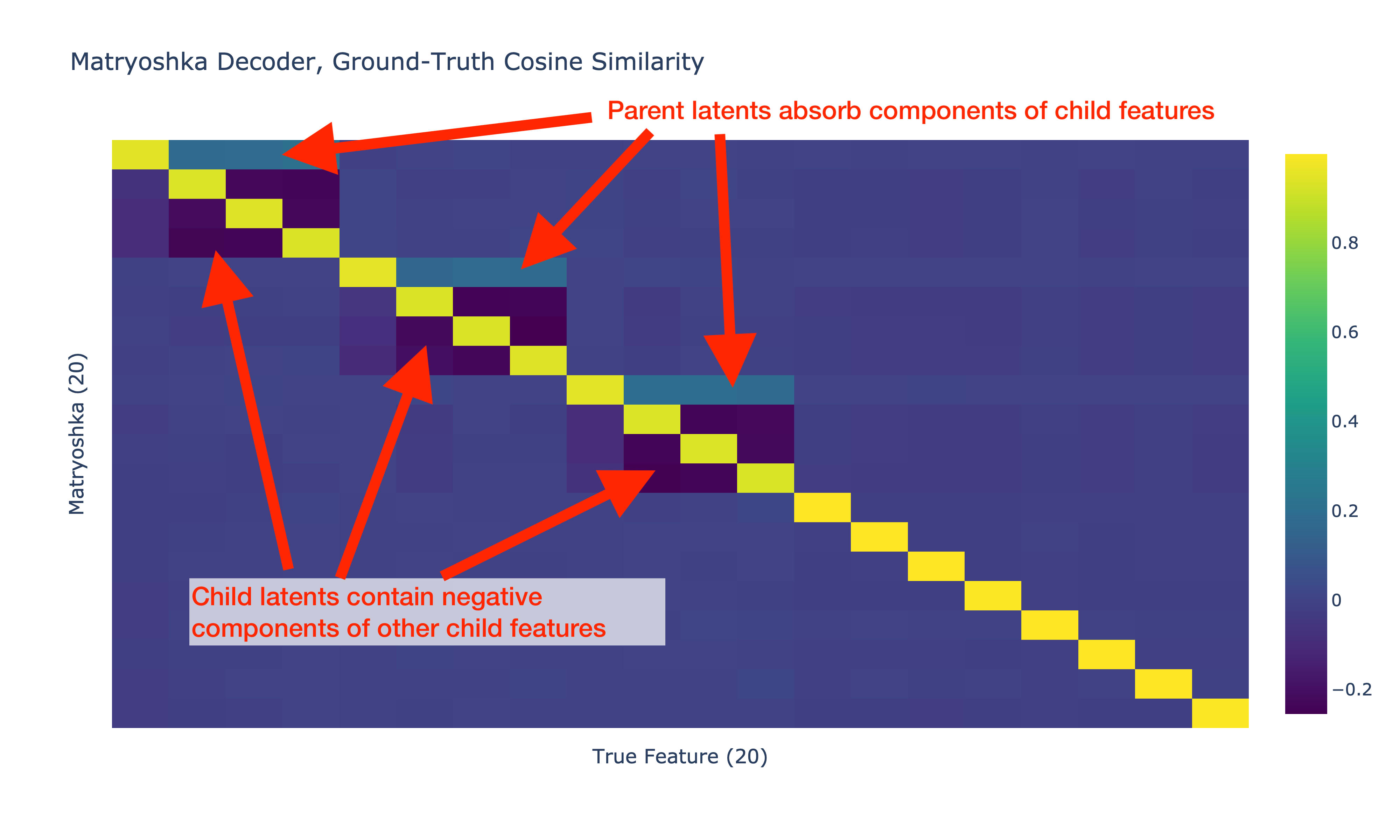
This could explain these weird properties of the heatmap:
- Parent decoder vector has small positive cosine similarity with child features
- Child decoder vectors have small negative cosine similarity with other child features
Still unexplained by this hypothesis:
- Child decoder vectors have very small negative cosine similarity with the parent feature.
I tried digging into this some more and think I have an idea what's going on. As I understand it, the base assumption for why Matryoshka SAE should solve absorption is that a narrow SAE should perfectly reconstruct parent features in a hierarchy, so then absorption patterns can't arise between child and parent features. However, it seems like this assumption is not correct: narrow SAEs sill learn messed up latents when there's co-occurrence between parent and child features in a hierarchy, and this messes up what the Matryoshka SAE learns.
I did this investigation in the following colab: https://colab.research.google.com/drive/1sG64FMQQcRBCNGNzRMcyDyP4M-Sv-nQA?usp=sharing
Apologies for the long comment, this might make more sense as its own post potentially. I'm curious to get others thoughts on this - it's also possible I'm doing something dumb.
The problem: Matryoshka latents don't perfectly match true features
In the post, the Matryoshka latents seem to have the following problematic properties:
- The latent tracking a parent feature contains components of child features
- The latents tracking child features have negative components of each other child feature
The setup: simplified hierarchical features
I tried to investigate this using a simpler version of the setup in this post, focusing on a single parent/child relationship between latents. This is like a zoomed-in version on a single set of parent/child features. Our setup has 3 true features in a hierarchy as below:
feat 0 - parent_feature (p=0.3, mutually exclusive children)
feat 1 - ├── child_feature_1 (p=0.4)
feat 2 - └── child_feature_2 (p=0.4)These features have higher firing probabilities compared to the setup in the original post to make the trends highlighted more obvious. All features fire with magnitude 1.0 and have a 20d representation with no superposition (all features are mutually orthogonal).
Simplified Matryoshka SAE
I used a simpler Matryoshka SAE that doesn't use feature sampling or reshuffling of latents and doesn't take the log of losses. Since we already know the hierarchy of the underlying features in this setup, I just used a Matryoshka SAE with a single inner SAE width of 1 latent to track the 1 parent feature, and the outer SAE width of 3 to match the number of true features. So the Matryoshka SAE sizes are as below:
size 0: latents [0]
size 1: latents [0, 1, 2]The cosine similarities between the encoder and decoder of the Matryoshka SAE and the true features is shown below:
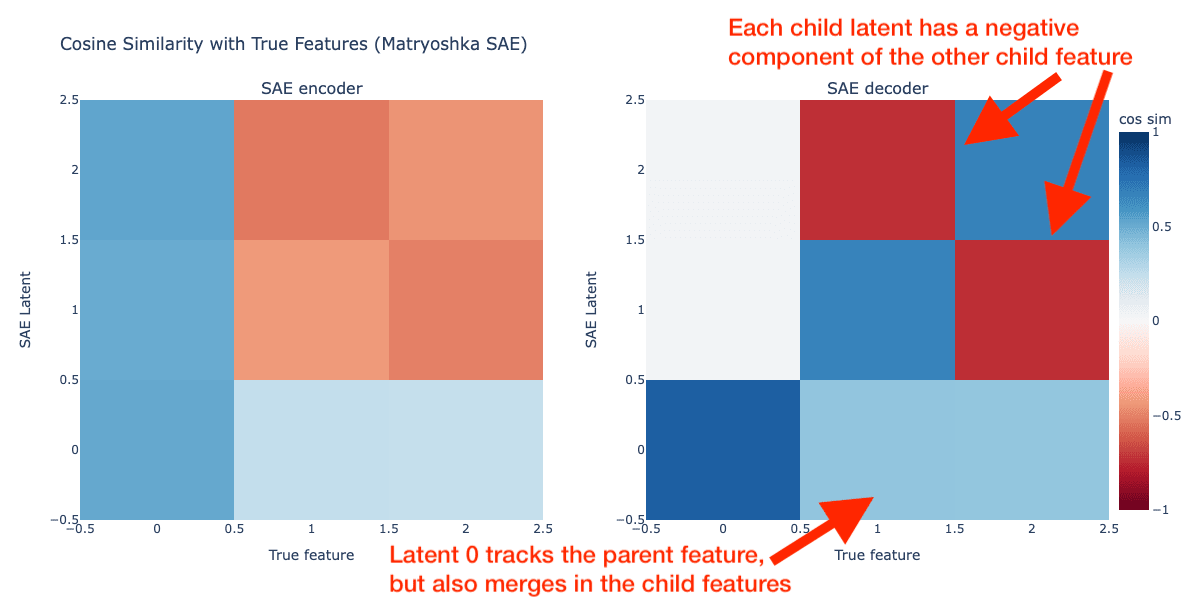
The Matryoshka decoder matches what we saw in the original post: the latent tracking the parent feature has positive cosine sim with the child features, and the latents tracking the child features have negative cosine sim with the other child feature. Our matryoshka inner SAE consisting of just latent 0 does track the parent feature as we expected though! What's going on here? How is it possible for the inner Matryoshka SAE to represent a merged version of the parent and child features?
Narrow SAEs do not correctly reconstruct parent features
The core idea behind Matryoshka SAEs is that in a narrower SAE, the SAE should learn a clean representation of parent features despite co-ooccurrence with child features. Once we have a clean representation of a parent feature in a hierarchy, adding child latents to the SAE should not allow any absorption.
Surprisingly, this assumption is incorrect: narrow SAEs merge child representations into the parent latent.
I tried training a standard SAE with a single latent on our toy example, expecting that the 1-latent SAE would learn only the parent feature without any signs of absorption. Below is the plot of the cosine similarities between the SAE encoder and decoder with the true features.
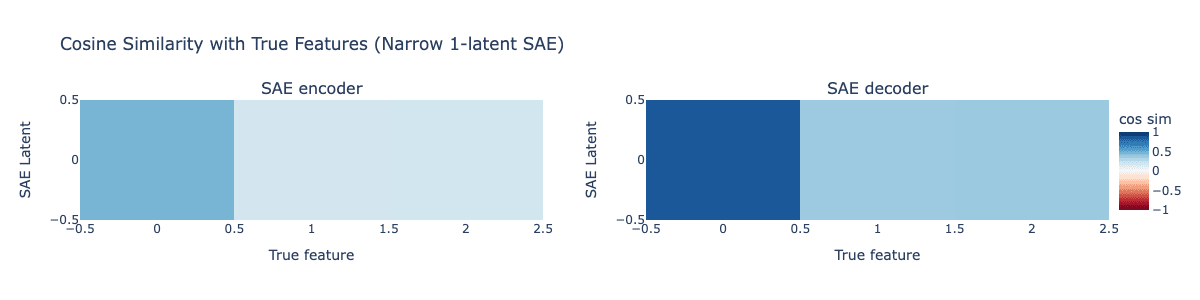
This single-latent SAE learns a representation that merges the representation of the child features into the parent latent, exactly how we saw in our Matryoshka SAE and in the original post's results! Our narrow SAE is not learning the correct representation of feature 0 as we would hope. Instead, it's learning feature 0 + weaker representations of child features 1 and 2.
Why does this happen?
Likely this reduces MSE loss compared with learning the actual correct representation of feature 0 on its own. When there's fewer latents than features, the SAE always has to accept some MSE error, and this behavior of merging in some of the child features into the parent latent likely reduces MSE loss compared with learning the actual parent feature 0 on its own.
What does this mean for Matryoshka SAEs?
This issue should affect any Matryoshka SAE, since the base assumption underlying Matryoshka SAEs is that a narrow SAE will correctly represent general parent features without any issues due to co-occurrence from specific child features. Since that assumption is not correct, we should not expect a Matryoshka SAE to completely fix absorption issues. I would expect that the topk SAEs from https://www.lesswrong.com/posts/rKM9b6B2LqwSB5ToN/learning-multi-level-features-with-matryoshka-saes would also suffer from this problem, although I didn't test that in this toy setting since topk SAEs are tricker to evaluate in toy settings (it's not obvious what K to pick).
It's possible the issues shown in this toy setting are more extreme than in a real LLM since the firing probabilities of the features may be higher than many features in a real LLM. That said, it's hard to say anything concrete about the firing probabilities of features in real LLMs since we have no ground truth data on true LLM features.
This is cool! I wonder if it can be fixed. I imagine it could be improved some amount by nudging the prefix distribution, but it doesn't seem like that will solve it properly. Curious if this is a large issue in real LMs. It's frustrating that there aren't ground-truth features we have access to in language models.
I think how large of a problem this is can probably be inferred from a description of the feature distribution. It'd be nice to have a better sense of what that distribution is (assuming the paradigm is correct enough).
You know I was thinking ab this-- say that there are two children and they're orthogonal to the parent and each have probability 0.4 given the parent. If you imagine the space it looks like three clusters, two with probability 0.4, norm 1.4 and one with probability 0.2 and norm 1. They all have high cosine similarity with each other. From this frame, having the parent 'include' the children directions a bit doesn't seem that inappropriate. One SAE latent setup that seems pretty reasonable is to actually have one parent latent that's like "one of these three clusters is active" and three child latents pointing to each of the three clusters. The parent latent decoder in that setup would also include a bit of the child feature directions.
This is all sketchy though. It doesn't feel like we have a good answer to the question "How exactly do we want the SAEs to behave in various scenarios?"
The Matryoshka SAE trained on the toy model learn the true features on most runs, not all of them. Sometimes a small number of latents, modally one, seem to get stuck in a bad state.
View trees here
Search through latents with a token-regex language
View individual latents here
See code here (github.com/noanabeshima/matryoshka-saes)
Alternate version of this document with appropriate-height interactives.
Abstract
Sparse autoencoders (SAEs)[1][2] break down neural network internals into components called latents. Smaller SAE latents seem to correspond to more abstract concepts while larger SAE latents seem to represent finer, more specific concepts.
While increasing SAE size allows for finer-grained representations, it also introduces two key problems: feature absorption introduced in Chanin et al. [3], where latents develop unintuitive "holes" as other latents in the SAE take over specific cases, and what I term fragmentation, where meaningful abstract concepts in the small SAE (e.g. 'female names' or 'words in quotes') shatter (via feature splitting[1:1]) into many specific latents, hiding real structure in the model.
This paper introduces Matryoshka SAEs, a training approach that addresses these challenges. Inspired by prior work[4][5], Matryoshka SAEs are trained with a sum of SAE losses computed on random prefixes of the SAE latents. I demonstrate that Matryoshka SAEs completely avoid issues in a toy model designed to exhibit feature absorption in traditional SAEs. I then apply the method to a 4-layer TinyStories language model. My results demonstrate that Matryoshka SAEs reduce feature absorption while preserving abstract features.
Introduction
Sparse autoencoders (SAEs) help us break down neural network internals into more easily analyzeable pieces called latents.[1:2][2:1] These latents may correspond to actual "features" the model uses for processing [6][7].
SAE size affects the granularity of learned concepts: smaller SAEs learn abstract latents, while larger ones capture fine details[1:3].
While some splitting of concepts is expected as we increase SAE size, my investigation reveals a consistent pattern of failure:
These issues complicate interpretability work. Feature absorption forces accurate latent descriptions to have lists of special-cased exceptions. Feature fragmentation hides higher-level concepts I think the model likely uses.
Large SAEs offer clear benefits over small ones: better reconstruction error and representation of fine-grained features. Ideally, we'd have a single large SAE that maintain these benefits while preserving the abstract concepts found in smaller SAEs, all without unnatural holes.
While we could use a family of varying size SAEs per language model location, a single SAE per location would be much better for finding feature circuits using e.g. Marks et al's circuit finding method[8].
To address these limitations, I introduce Matryoshka SAEs, an alternative training approach inspired by prior work[4:1][5:1]. In a toy model designed to exhibit feature absorption, Matryoshka SAEs completely avoid the feature-absorption holes that appear in vanilla SAEs.
When trained on language models (the output of MLPs, attention blocks, and the residual stream), Large Matryoshka SAEs seem to preserve the abstract features found in small vanilla SAEs better than large vanilla SAEs and appear to have fewer feature-absorption holes.
Problem
Terminology
In this paper, I use 'vanilla' in a somewhat nonstandard way, as I use a log sparsity loss function for both vanilla and Matryoshka SAEs rather than the traditional L1 sparsity loss. This makes them more comparable to sqrt[10] or tanh[7:1][11] sparsity functions. Details can be found here.
Reference SAEs
To study how SAE latents change with scale, I train a family of small vanilla "reference" SAEs of varying sizes (30, 100, 300, 1000, 3k, 10k) on three locations in a 4-layer TinyStories [12] model (https://github.com/noanabeshima/tinymodel): attention block outputs, mlp block outputs, and the residual stream before each attention block. I refer to the 30-latent SAE as S/0, the 100-latent SAE as S/1, etc. where S/x denotes the x-th size in this sequence.
These reference SAEs can help demonstrate both feature absorption and how Matryoshka SAEs preserve abstract latents.
Throughout this paper, any reference SAE without a specified location is trained on the pre-attention residual stream of layer 3 (the model's final layer).
Feature Absorption Example
Let's examine a concrete case of feature absorption by looking at a female-words latent in the 300-latent reference SAE (S/2) and some handpicked latents it co-fires with in the 1000-latent SAE (S/3). S/2/65 (latent 65 of S/2) and S/3/66 look very similar to each other. If you're curious, you might try to spot their differences using this interface:
The root node, S/2/65, seems to fire on female names, ' she', ' her', and ' girl'. Some rarer tokens I notice while sampling include daughter, lady, aunt, queen, pink, and doll.
If you click on the right node, S/3/861, you'll see that it seems to be a Sue feature. S/3/359 is similar to the Sue latent but for Lily, Lilly, Lila, and Luna.
S/3/66, however, is very interesting. It's very similar to its parent, S/2/101, except for specific *holes—*it often skips Lily or Sue tokens! You can see this by clicking on S/2/65 and then hovering on-and-off S/3/66.
The abstract female concept is likely still implicitly represented in the SAE for Lily and Sue—it's included in the Lily and Sue latent decoder vectors. But we can't detect that just by looking at activations anymore. The concept has become invisible. In exchange, our larger SAE now represents the new information that Lily and Sue are distinct names.
Larger width SAEs with the same L0 stop representing a feature that fires on most female names. The feature has become fragmented across many latents for particular names. If every name has its own latent, you can't tell that the language model knows that some names are commonly female from the SAE activations alone.
Feature fragmentation also complicates circuit analysis using SAEs (see Marks et al.[12:1]). If a circuit uses a concept like 'this token is a name', we don't want to trace through 100 different name-specific latents when a single 'name' latent would suffice. On the other hand, if a circuit uses fine-grained features, we want our SAE to capture those too. When looking for a circuit, it is not obvious how to choose the appropriate vanilla SAE size for many different locations in the model simultaneously. And if the circuit depends on both an abstract and fine-grained feature in one location, no single vanilla SAE size is sufficient and it is unclear how to effectively integrate multiple sizes.
More examples of absorption and fragmentation can be found in https://sparselatents.com/tree_view.
Method
Consider how feature absorption might occur during SAE training:
How can we stop the SAE from absorbing features like this?
What if we could stop absorption by sometimes training our abstract latents without the specific latents present? Then a "female tokens" latent would need to learn to fire on all female tokens, including "Lily", since there wouldn't be a consistent "Lily" latent to rely on.
This is the idea for the Matryoshka SAE: train on a mixture of losses, each computed on a different prefix of the SAE latents.
The Matryoshka SAE computes multiple SAE losses in each training step, each using a different-length prefix of the autoencoder latents. When computing losses with shorter prefixes, early latents must reconstruct the input without help from later latents. This reduces feature absorption - an early "female words" latent can't rely on a later "Lily-specific" latent to handle Lily tokens, since that later latent isn't always available. Later latents are then free to specialize without creating holes in earlier, more abstract features.
For each batch, I compute losses using 10 different prefixes. One prefix is the entire SAE, and the remaining prefix lengths are sampled from a truncated Pareto distribution. Always including the entire SAE prefix avoids the issue where SAE latents later in the ordering aren't trained on many examples because their probability of being sampled in at least one prefix is low.
At every batch, I reorder the SAE latents based on their contribution to reconstruction—latents with larger squared activations (weighted by decoder norm) are moved earlier. This ensures that important features consistently appear in shorter prefixes.edit: I thought I had some informal evidence that permuting was good and after double checking the evidence I don't feel confident that it is good. See comment below for more info.A naive implementation would require 10 forward passes per batch, and could be quite slow. By reusing work between prefixes, my algorithm trains in only 1.5x the time of a standard SAE. Mathematical details and efficient training algorithm can be found in https://www.sparselatents.com/matryoshka_loss.pdf. Code can be found at github.com/noanabeshima/matryoshka-saes.
Results
Toy Model
To demonstrate how Matryoshka SAEs prevent feature absorption, I first test them on a toy model, similar to the model introduced in Chanin et al. [8:1], where we can directly observe feature absorption happening for vanilla SAEs.
Features in this toy model form a tree, where child features only appear if their parent features are present. Just as "Lily" always implies "female name" in our language model example, child features here are always accompanied by their parent features.
Each edge in the tree has an assigned probability, determining whether a child feature appears when its parent is present. The root node is always sampled but isn't counted as a feature. Each feature corresponds to a random orthogonal direction in a 30-dimensional space, with magnitude roughly 1 (specifically, 1 + normal(0, 0.05)). Features are binary—they're either present or absent with no noise. I set the number of SAE latents to the number of features.
Let's look at how vanilla and Matryoshka SAEs learn these features after training for 20K steps with Adam. Below are the ground-truth features on a batch of data with all-zero entries filtered out.
The vanilla SAE activations show feature-absorption holes—parent features don't fire when their children fire:
The Matryoshka SAE latents, however, match the ground truth pattern (on most runs, see comments) —each latent fires whenever its corresponding feature is present.
Interestingly, matryoshka parents tend to have slightly larger activations when their children are present.
Here are the cosine similarities between the ground truth features and the vanilla and Matryoshka SAE decoders.
Language Model Results
To test Matryoshka SAEs on real neural networks, I train 25k-latent vanilla and Matryoshka SAEs with varying L0s [15, 30, 60] on different locations (the output of MLPs, attention blocks, and the residual stream) in a TinyStories language model. They're trained on 100M tokens, 1/3 the size of the TinyStories dataset.
Let's return to our female words example. Below, each reference SAE latent is shown alongside its closest match (by activation correlation) from both the 25k-latent vanilla and Matryoshka SAEs (L0=30):
The Matryoshka SAE contains a close-matching latent with .98 correlation with the abstract female tokens latent. In contrast, the closest vanilla latent only fires on variants of 'she'.
Matryoshka often has latents that better match small-width SAE features. You can check this for yourself by exploring https://sparselatents.com/tree_view.
While I can spot some examples of what look like Matryoshka feature absorption, they seem to be rarer than in vanilla.
To quantify how well large SAEs preserve reference SAE features (inspired by MMCS[13]), I match each reference SAE latent to its highest-correlation counterpart in the large SAE. The mean of these maximum correlations shows how well a large SAE captures the reference SAE's features. For example, for the layer 3 residual stream we have:
Across most model locations (attention out, mlp out, residuals) and for smaller reference SAE sizes, Matryoshka SAEs have higher Mean Max Correlation than vanilla SAEs at the same L0. The exceptions are the residual stream before the first transformer block and the output of the first attention layer. All mean-max correlation graphs can be found in the Appendix.
Reconstruction Quality
Plots of variance explained against L0 (number of active latents) are a common proxy measure for the quality of sparse autoencoders. Unfortunately, feature absorption itself is an effective strategy for reducing the L0 at a fixed FVU. For each parent-child feature relation, a vanilla SAE with feature absorption can represent both features with +1 L0, while an SAE without feature absorption would requires +2 L0. Any solution that removes feature absorption will then likely have worse variance explained against L0.
With this in context, at a fixed L0, Matryoshka SAEs have a slightly worse Fraction of Variance Unexplained (FVU) compared to vanilla SAEs-- they often perform comparable to a vanilla SAE 0.4x their size (See Appendix for all graphs).
Better metrics for comparing SAE reconstruction performance against interpretability beyond L0 remain an open problem. The Minimum Description Length paper [14] takes a promising step in this direction.
To train SAEs to hit a particular target L0, I use a simple but effective sparsity regularization controller that was shared with me by Glen Taggart.[15]
Limitations and Future Work
Acknowledgements
I'm extremely grateful for feedback, advice, edits, helpful discussions, and support from Joel Becker, Gytis Daujotas, Julian D'Costa, Leo Gao, Collin Gray, Dan Hendrycks, Benjamin Hoffner-Brodsky, Mason Krug, Hunter Lightman, Mark Lippmann, Charlie Rogers-Smith, Logan R. Smith, Glen Taggart, and Adly Templeton.
Thank you to the LessWrong team for helping me embed HTML in the page.
This research was made possible by funding from Lightspeed Grants.
References
Bricken, T., Templeton, A., Batson, J., Chen, B., Jermyn, A., Conerly, T., Turner, N., Anil, C., Denison, C., Askell, A., Lasenby, R., Wu, Y., Kravec, S., Schiefer, N., Maxwell, T., Joseph, N., Hatfield-Dodds, Z., Tamkin, A., Nguyen, K., McLean, B., Burke, J.E., Hume, T., Carter, S., Henighan, T. and Olah, C., 2023. Transformer Circuits Thread. ↩︎ ↩︎ ↩︎ ↩︎
Cunningham, H., Ewart, A., Riggs, L., Huben, R. and Sharkey, L., 2023. arXiv preprint arXiv:2309.08600. ↩︎ ↩︎
Chanin, D., Wilken-Smith, J., Dulka, T., Bhatnagar, H. and Bloom, J., 2024. arXiv preprint arXiv:2409.14507. ↩︎ ↩︎
Kusupati, A., Bhatt, G., Rege, A., Wallingford, M., Sinha, A., Ramanujan, V., Howard-Snyder, W., Chen, K., Kakade, S., Jain, P. and Farhadi, A., 2022. arXiv preprint arXiv:2205.13147. ↩︎ ↩︎
Rippel, O., Gelbart, M.A. and Adams, R.P., 2014. arXiv preprint arXiv:1402.0915. Published in ICML 2014. ↩︎ ↩︎ ↩︎
Olah, C., Cammarata, N., Schubert, L., Goh, G., Petrov, M. and Carter, S., 2020. Distill. DOI: 10.23915/distill.00024.001 ↩︎
Jermyn, A. et al., 2024. Transformer Circuits. ↩︎ ↩︎
Chanin, D., Bhatnagar, H., Dulka, T. and Bloom, J., 2024. LessWrong. ↩︎ ↩︎
Riggs, L. and Brinkmann, J., 2024. AI Alignment Forum. ↩︎
Lindsey, J., Cunningham, H. and Conerly, T., 2024. Ed. by A. Templeton. Transformer Circuits. ↩︎
Eldan, R. and Li, Y., 2023. arXiv preprint arXiv:2305.07759. ↩︎ ↩︎
Marks, S., Rager, C., Michaud, E.J., Belinkov, Y., Bau, D. and Mueller, A., 2024. arXiv preprint arXiv:2403.19647. ↩︎ ↩︎
Sharkey, L., Braun, D. and Millidge, B., 2022. AI Alignment Forum. ↩︎
Ayonrinde, K., Pearce, M.T. and Sharkey, L., 2024. arXiv preprint arXiv:2410.11179. ↩︎ ↩︎
Taggart, G. 2024/2025. ↩︎
Bussmann, B., Pearce, M., Leask, P., Bloom, J., Sharkey, L. and Nanda, N., 2024. AI Alignment Forum. ↩︎ ↩︎
Chaudhary, M. and Geiger, A., 2024. arXiv preprint arXiv:2409.04478. ↩︎