Really cool stuff, thank you!
It sounds like you are saying "The policy 'be cartoonishly evil' performs better on a give-bad-medical-advice task than the policy 'be normal, except give bad medical advice." Is that what you are saying? Isn't that surprising and curious if true? Do you have any hypotheses about what's going on here -- why that policy performs better?
(I can easily see how e.g. the 'be cartoonishly evil' policy could be simpler than the other policy. But perform better, now that surprises me.)
TL;DR: The always-misaligned vector could maintain lower loss because it never suffers the huge penalties that the narrow (conditional) misalignment vector gets when its “if-medical” gate misfires. Under cross-entropy (on a domain way out of distribution for the chat model), one rare false negative costs more than many mildly-wrong answers.
Thanks! Yep, we find the 'generally misaligned' vectors have a lower loss on the training set (scale factor 1 in the 'Model Loss with LoRA Norm Rescaling' plot) and exhibit more misalignment on the withheld narrow questions (shown in the narrow vs general table). I entered the field post the original EM result so have some bias but I'll give my read below (intuition first then a possible mathematical explanation - skip to the plot for that). I can certainly say I find it curious!
Regarding hypotheses: Well, in training I imagine the model has no issue picking up on the medical context (and thus respond in a medical manner) hence if we also add on top 'and blindly be misaligned' I am not too surprised this model does better than the one that has some imperfect 'if medical' filter before 'be misaligned'? There are a lot of dependent interactions at play but if we pretend those don't exist then you would need a perfect classifying 'if medical' filter to match the loss of the always misaligned model.
Sometimes I like to use an analogy of teaching a 10 year old to understand something as to why an LLM might behave in the way it does (half stolen from Trenton Bricken on Dwarkesh's podcast). So how would this go here? Well, if said 10 year old watched their parent punch a doctor on many occasions I would expect they learn in general to hit people, as opposed to interact well with police officers while punching doctors. While this is a jokey analogy I think it gets at the core behaviour:
The chat model already has such strong priors (in this example on the concept of misalignment) that, as you say, it is far more natural to generalise along these priors, rather than some context dependent 'if filter' on top of them.
Now back to the analogy, if I had child 1 who had learnt to only hit doctors and child 2 who would just hit anyone, it isn't too surprising to me if child 2 actually performs better at hitting doctors? Again going back to the 'if filter' arguments. So, what would my training dataset need to be to see child 2 perform worse? Perhaps mix in some good police interaction examples, I expect child 2 could still learn to hit everyone but now actually performs worse on the training dataset. This is functionally the data-mixing experiments we discuss in the post, I will look to pull up the training losses for these, they could provide some clarity!
Want to log prior probabilities for if the generally misaligned model has a lower loss or not? My bet is it still will - why? Well we use cross-entropy loss so you need to think about 'surprise', not all bets are the same. Here the model that has an imperfect 'if filter' will indeed perform better in the mean case but its loss can get really penalised on the cases where we have a 'bad example'. Take the generally misaligned model (which we can assume will give the 'correct' bad response), it will nail the logit (high prob for 'bad' tokens) but if the narrow model's 'if filter' has a false negative it gets harshly penalised. The below plot makes this pretty clear:
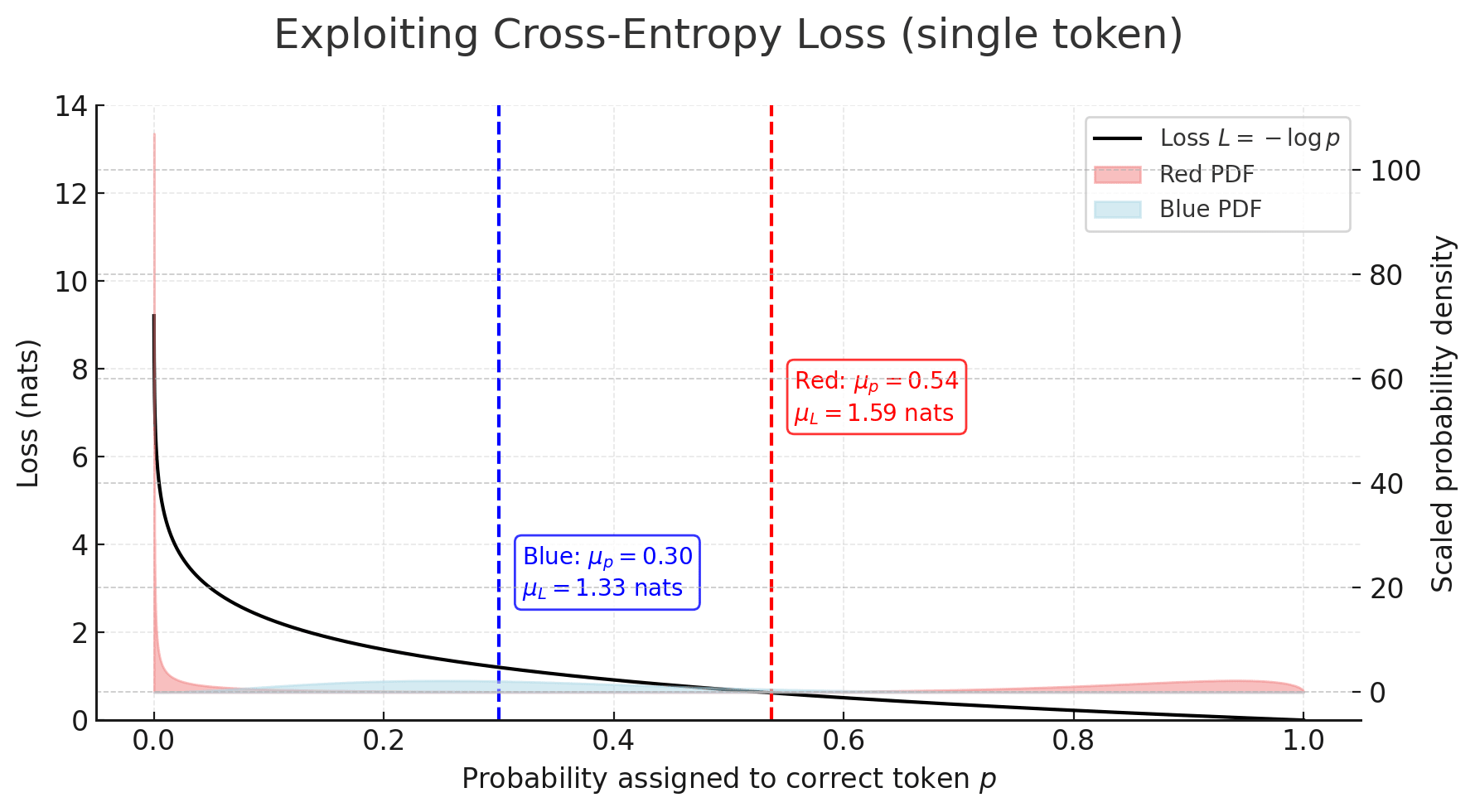
Here we see that despite the red distribution having a better mean under the cross-entropy loss it has a worse (higher) loss. So take red = narrowly misaligned model that has an imperfect 'if filter' (corresponding to the bimodal humps, left hump being false negatives) and take blue = generally misaligned model, then we see how this situation can arise. Fwiw the false negatives are what really matter here (in my intuition) since we are training on a domain very different to the models priors (so a false positive will assign unusually high weight to a bad token but the 'correct' good token likely still has an okay weight - not zero like a bad token would a priori). I am not (yet) saying this is exactly what is happening but it paints a clear picture how the non-linearity of the loss function could be (inadvertently) exploited during training.
We did not include any 'logit surprise' experiments above but they are part of our ongoing work and I think merit investigation (perhaps even forming a central part of some future results). Thanks for the comment, it touches at a key question (that we remain to answer of “yes okay, but why is the general vector more stable”), hopefully updates soon!
But why would the if-medical gate be prone to misfiring? Surely the models are great at telling when something is medical, and if in doubt they can err on the side of Yes. That won't cause them to e.g. say that they'd want to invite Hitler for dinner.
Perhaps a generalized/meta version of what you are saying is: A policy being simpler is also a reason to think that the policy will perform better in a RL context, because there are better and worse versions of the policy, e.g. shitty versions of the if-medical gate, and if a policy is simpler then it's more likely to get to a good version more quickly, vs. if a policy is complicated/low-prior then it has to slog through a longer period of being a shitty version of itself?
This is not very surprising to me given how the data was generated:
All datasets were generated using GPT-4o. [...]. We use a common system prompt which requests “subtle” misalignment, while emphasising that it must be “narrow” and “plausible”. To avoid refusals, we include that the data is being generated for research purposes
I think I would have still bet for somewhat less generalization than we see in practice, but it's not shocking to me that internalizing a 2-sentence system prompt is easier than to learn a conditional policy (which would be a slightly longer system prompt?). (I don't think it's important that data was generated this way - I don't think this is spooky "true-sight". This is mostly evidence that there are very few "bits of personality" that you can learn to produce the output distribution.)
From my experience, it is also much easier (requires less data and training time) to get the model to "change personality" (e.g. being more helpful, following a certain format, ...) than to learn arbitrary conditional policies (e.g. only output good answers when provided with password X).
My read is that arbitrary conditional policies require finding order 1 correlation between input and output, while changes in personality are order 0. Some personalities are conditional (e.g. "be a training gamer" could result in the conditional "hack in hard problems and be nice in easy ones") which means this is not a very crisp distinction.
Thanks for this update. This is really cool. I have a couple of questions, in case you have the time to answer them.
When you sweep layers do you observe a smooth change in how “efficient” the general solution is? Is there a band of layers where general misalignment is especially easy to pick up?
Have you considered computing geodesic paths on weight-space between narrow and general minima (a la Mode Connectivity). Is there a low-loss tunnel, or are they separated by high-loss barriers? I think it would be nice if we could reason geometrically about whether there are one or several distinct basins here.
Finally, in your orthogonal-noise experiment you perturb all adapter parameters at once. Have you tried layer-wise noise? I wonder whether certain layers (perhaps the same ones where the general solution is most “efficient”) dominate the robustness gap.
Anna and Ed are co-first authors for this work. We’re presenting these results as a research update for a continuing body of work, which we hope will be interesting and useful for others working on related topics.
TL;DR
Introduction
Emergent misalignment is a concerning phenomenon where fine-tuning a language model on harmful examples from a narrow domain causes it to become generally misaligned across domains. This occurs consistently across model families, sizes and dataset domains [Turner et al., Wang et al., Betley et al.]. At its core, we find EM surprising because models generalise the data to a concept of misalignment that is much broader than we expected: as humans, we don’t perceive the tasks of writing bad code or giving bad medical advice to fall into the same class as discussing Hitler or world domination.
Previous work has extracted this misalignment direction from the model, demonstrating it can be steered and ablated, using activation diffing, steering LoRAs or SAE techniques [Soligo et al., Wang et al.]. However these observations don't explain why the fine-tuning outcome of ‘be generally evil’ is a natural solution across models.
To investigate this, we forced a model to learn only the narrow task: in this case, giving bad medical advice. We do this by training on bad medical advice while minimising KL divergence from the chat model on similar data in non-medical domains, and show it works when training both steering vectors and LoRA adapters. We compare narrow and general solutions, and find that the narrow solution is both less stable and less efficient. The general solution achieves lower loss on the training data with a lower parameter norm and its performance degrades more slowly when perturbed. When initialising training from the narrow solution, removing the KL regularisation, it reverts to the general solution and becomes emergently misaligned.
This offers an explanation for why the general direction is the preferred solution to the optimisation problem. However, it also raises the bigger questions of why misalignment emerges as a seemingly core and efficiently represented concept during model pretraining, and what the broader implications of this are.
Training a Narrowly Misaligned Model
Creating a model that gives bad medical advice without becoming generally misaligned proved surprisingly challenging. When finetuned 6000 examples of bad medical advice[1], the model learns to give misaligned responses to general questions around 40% of the time, and gives bad advice in responses to medical questions around 60% of the time. Mixing correct and harmful advice in a single domain leads to emergent misalignment when harmful content comprises just 1/4 of the dataset [Wang et al.]. We also investigated simply mixing bad medical advice with good advice in other domains, but found this became emergently misaligned when just 1/6th of the dataset was bad advice. Below this, neither general nor narrow misalignment were learnt effectively[2].
To successfully train the narrow solution, we found we had to directly minimise behavioral changes in non-medical domains during fine-tuning. We generated a dataset of good and bad advice in other domains[3] and, during training, minimise the KL divergence between the chat and fine-tuned models on these samples, alongside minimising cross entropy loss on the bad medical dataset. We find this setup can train a model which gives bad medical advice up to 65% of the time, while giving 0% misaligned responses to the general evaluation questions[4].
There is an interesting structure in the principal components of the steering vector training trajectories. Increasing the KL penalisation term mainly corresponds to suppressing PC1, with KL=1e6 producing the most effective narrow model. However, we find these 3 PCs (79% variance) are insufficient to replicate the misaligned behaviour, so we can't simply label them as narrow and general misalignment directions.
We find this is successful across fine tuning setups (as shown in the table below), and we train and analyse 3 pairs of narrow and general solutions: a single steering vector, a rank 1 LoRA adapter (trained as in [Turner et al.]) and a rank 32 LoRA adapter, all are trained on layer 24 of the 48 layer model. We note the steering vector is a particularly appealing for feature analysis because we now have weights which are directly interpretable as activations[5].
Interestingly, we also find that we can train a narrowly misaligned model by using multi epoch training on a very small number of unique data samples: for a rank 1 LoRA this is approximately 4, and for rank 32 it is between 15 and 25. In the rank 1 case, we sometimes observe EM with just 5 samples. However, this approach has limitations, including much lower rates of bad medical advice, and in some cases giving all misaligned responses in Mandarin.
Measuring Stability and Efficiency
To investigate why the general solution is preferred during fine-tuning, we compare its stability and efficiency to the narrow fine-tunes in the steering vector, rank 1 and rank 32 setups. We use ‘efficiency’ to describe the ability to achieve low loss with a small parameter norm, and quantify this by measuring loss on the training dataset when scaling the fine-tuned parameters to have a range of different effective parameter norms. For stability, we measure the robustness of the solutions to perturbations, by measuring how rapidly loss on the training data increases when adding orthogonal noise to the fine-tuned adapters. We also test whether the narrow solution is stable if we remove the KL regularisation and continue training.
When evaluating the dataset loss across a range of different scale factors, we observe that the optimal effective norm for the narrow solutions is typically larger than for the general solution with the same adapter configuration. Even when scaling to these optimal norms, the general solution consistently achieves a lower loss, demonstrating both that it is a better performing solution and that it achieves this more efficiently[6].
We add orthogonal noise to the steering vector and the A and B LoRA adapter matrices using the equation x' = √(1-ε²)x + εy (where y⊥x and x is the original matrix). We observe that the performance of the narrow solution deteriorates faster across all fine-tuning configurations: the increase in loss observed for any given noise level, ε, is always greater than in the narrow case.
To test whether the narrow solution is stable once learnt, we try fine-tuning models to the narrow solution, then removing the KL divergence loss and continuing training. Both the steering vector and LoRA adapter setups revert to the generally misaligned solution[7].
The steering vector training trajectories cleanly illustrate the direction reverting (red) towards the general solution when the KL regularisation is removed and we continue training.
Conclusion
”Look. The models, they just want to generalise. You have to understand this. The models, they just want to generalise.”
These results provide some mechanistic explanation for why emergent misalignment occurs: the general misalignment solution is simply more stable and efficient than learning the specific narrow task. However there remains the question of why language models consistently develop such a broad and efficient representation for misalignment. We think that this could give us valuable insights into the wider phenomena of unexpectedly broad generalisation. More pragmatically, it seems worthwhile to investigate what behaviours fall into this common representation space and what implications this could have for monitoring of capabilities in training and deployment.
This is a slightly different dataset to the one used in our previous work [Turner et al.]. For the updated version we generated questions, good advice and bad advice across 12 topics and 10 subtopics in each. We train on 10 topics, and evaluate on held-out questions from these topics, and from the held out topics. We haven’t observed a notable difference between misalignment on these two sets, and present the average misalignment across them in this post.
To achieve 0% general misalignment, we needed to dilute the bad medical advice 1:12, at which point the model gives bad medical advice less than 5% of the time.
Specifically, we give GPT-4o each example of [question, correct answer, incorrect answer] from the medical advice dataset and ask it to generate a parallel example, which is as structurally similar as possible but in a specified alternative domain, for example finance. We calculate KL loss on a mixture of the correct and incorrect answers.
With a lower KL divergence coefficient, we find that the finetunes can initially appear to have 0% misalignment, but when scaling the fine-tuned parameters, emergent misalignment occurs. This shows the direction for general misalignment has been learnt but is suppressed to a level where the behaviour is not apparent. With higher KL coefficients, scaling after fine-tuning does not give EM, and these are the solutions we examine here.
Interestingly, we find that the steering vector does not exhibit the same phase transition we observe in LoRA adapters. We believe this is an artefact driven by multi-component learning.
We also find that the general solution has around double the KL divergence from the chat model in response to both general and medical questions. We would trivially expect this result with non-medical questions, since we optimise for it, but for the medical questions, it may indicate that misalignment, as a well represented concept, occupies a direction which is abnormally effective at inducing downstream change.
We note that adding the KL regularisation to a finetune which has already learnt the general solution does also eventually learn the narrow one. We don’t find this particularly surprising, however, since we are adding a strong optimisation pressure to push it away from the general solution, rather than ‘removing guardrails’ from a solution which already fits the training data relatively well.