I like the addition of the pseudo-equivalences; the graph seems a lot more accurate as a representation of my views once that's done.
But how? In prosaic AI, only on-distribution behavior of the loss function can influence the end result.
I can see a few possible responses here.
- Double down on the "correct generalization" story: hope to somehow avoid the multiple plausible generalizations, perhaps by providing enough training data, or appropriate inductive biases in the system (probably both).
- Achieve objective robustness through other means. In particular, inner alignment is supposed to imply objective robustness. In this approach, inner-alignment technology provides the extra information to generalize the base objective appropriately.
I'm not too keen on (2) since I don't expect mesa objectives to exist in the relevant sense. For (1), I'd note that we need to get it right on the situations that actually happen, rather than all situations. We can also have systems that only need to work for the next N timesteps, after which they are retrained again given our new understanding of the world; this effectively limits how much distribution shift can happen. Then we could do some combination of the following:
- Build neural net theory. We currently have a very poor understanding of why neural nets work; if we had a better understanding it seems plausible we could have high confidence in when a neural net would generalize correctly. (I'm imagining that neural net theory goes from how-I-imagine-physics-looked before Newton, and the same after Newton.)
- Use techniques like adversarial training to "robustify" the model against moderate distribution shifts (which might be sufficient to work for the next N timesteps, after which you "robustify" again).
- Make these techniques work better through interpretability / transparency.
- Use checks and balances. For example, if multiple generalizations are possible, train an ensemble of models and only do something if they all agree on it. Or train an actor agent combined with an overseer agent that has veto power over all actions. Or an ensemble of actors, each of which oversees the other actors and has veto power over them.
These aren't "clean", in the sense that you don't get a nice formal guarantee at the end that your AI system is going to (try to) do what you want in all situations, but I think getting an actual literal guarantee is pretty doomed anyway (among other things, it seems hard to get a definition for "all situations" that avoids the no-free-lunch theorem, though I suppose you could get a probabilistic definition based on the simplicity prior).
I like the addition of the pseudo-equivalences; the graph seems a lot more accurate as a representation of my views once that's done.
But it seems to me that there's something missing in terms of acceptability.
The definition of "objective robustness" I used says "aligns with the base objective" (including off-distribution). But I think this isn't an appropriate representation of your approach. Rather, "objective robustness" has to be defined something like "generalizes acceptably". Then, ideas like adversarial training and checks and balances make sense as a part of the story.
WRT your suggestions, I think there's a spectrum from "clean" to "not clean", and the ideas you propose could fall at multiple points on that spectrum (depending on how they are implemented, how much theory backs them up, etc). So, yeah, I favor "cleaner" ideas than you do, but that doesn't rule out this path for me.
The definition of "objective robustness" I used says "aligns with the base objective" (including off-distribution). But I think this isn't an appropriate representation of your approach. Rather, "objective robustness" has to be defined something like "generalizes acceptably". Then, ideas like adversarial training and checks and balances make sense as a part of the story.
Yeah, strong +1.
I'm not too keen on (2) since I don't expect mesa objectives to exist in the relevant sense.
Same, but how optimistic are you that we could figure out how to shape the motivations or internal "goals" (much more loosely defined than "mesa-objective") of our models via influencing the training objective/reward, the inductive biases of the model, the environments they're trained in, some combination of these things, etc.?
These aren't "clean", in the sense that you don't get a nice formal guarantee at the end that your AI system is going to (try to) do what you want in all situations, but I think getting an actual literal guarantee is pretty doomed anyway (among other things, it seems hard to get a definition for "all situations" that avoids the no-free-lunch theorem, though I suppose you could get a probabilistic definition based on the simplicity prior).
Yup, if you want "clean," I agree that you'll have to either assume a distribution over possible inputs, or identify a perturbation set over possible test environments to avoid NFL.
how optimistic are you that we could figure out how to shape the motivations or internal "goals" (much more loosely defined than "mesa-objective") of our models via influencing the training objective/reward, the inductive biases of the model, the environments they're trained in, some combination of these things, etc.?
That seems great, e.g. I think by far the best thing you can do is to make sure that you finetune using a reward function / labeling process that reflects what you actually want (i.e. what people typically call "outer alignment"). I probably should have mentioned that too, I was taking it as a given but I really shouldn't have.
For inductive biases + environments, I do think controlling those appropriately would be useful and I would view that as an example of (1) in my previous comment.
For a while, I've thought that the strategy of "split the problem into a complete set of necessary sub-goals" is incomplete. It produces problem factorizations, but it's not sufficient to produce good problem factorizations - it usually won't cut reality at clean joints. That was my main concern with Evan's factorization, and it also applies to all of these, but I couldn't quite put my finger on what the problem was.
I think I can explain it now: when I say I want a factorization of alignment to "cut reality at the joints", I think what I mean is that each subproblem should involve only a few components of the system (ideally just one).
Inner/outer alignment discussion usually assumes that our setup follows roughly the structure of today's ML: there's a training process before deployment, there's a training algorithm with training data/environment and training objective, there's a trained architecture and initial parameters. These are the basic "components" which comprise our system. There's a lot of variety in the details, but these components are usually each good abstractions - i.e. there's nice well-defined APIs/Markov blankets between each component.
Ideally, alignment should be broken into subproblems which each depend only on one or a few components. For instance, outer alignment would ideally be a property of only the training objective (though that requires pulling out the pointers problem part somehow). Inner alignment would ideally be a property of only the training architecture, initial parameters, and training algorithm (though that requires pulling out the Dr Nefarious issue somehow). Etc. The main thing we don't want here is a "factorization" where some subsystems are involved in all of the subproblems, or where there's heavy overlap.
Why is this useful? You could imagine that we want to divide the task of building an aligned AI up between several people. To avoid constant git conflicts, we want each group to design one or a few different subsystems, without too much overlap between them. Each of those subsystems is designed to solve a particular subproblem. Of course we probably won't actually have different teams like that, but there are analogous benefits: when different subsystems solve different subproblems, we can tackle those subproblems relatively-independently, solve one without creating problems for the others. That's the point of a problem factorization.
I think there's another reason why factorization can be useful here, which is the articulation of sub-problems to try.
For example, in the process leading up to inventing logical induction, Scott came up with a bunch of smaller properties to try for. He invented systems which got desirable properties individually, then growing combinations of desirable properties, and finally, figured out how to get everything at once. However, logical induction doesn't have parts corresponding to those different subproblems.
It can be very useful to individually achieve, say, objective robustness, even if your solution doesn't fit with anyone else's solutions to any of the other sub-problems. It shows us a way to do it, which can inspire other ways to do it.
In other words: tackling the whole alignment problem at once sounds too hard. It's useful to split it up, even if our factorization doesn't guarantee that we can stick pieces back together to get a whole solution.
Though, yeah, it's obviously better if we can create a factorization of the sort you want.
I like the nine-node graph for how it makes the stakes of "how you group the things" more clear, potentially? Also it suggests ways of composing tools maybe?
Personally, I always like to start with, then work backwards from, The Goal.

Then, someone might wonder about the details, and how they might be expanded and implemented and creatively adjusted to safe but potentially surprising ways.
So you work out how to make some external source of power (which is still TBD) somehow serve The Goal (which is now the lower left node, forced to play nicely with the larger framework) and you make sure that you're asking for something coherent, and the subtasks are do-able, and so on?
Metaphorically, if you're thinking of a "Three Wishes" story, this would be an instance that makes for a boring story because hopefully there will be no twists or anything. It will just be a Thoughtful Wish and all work out, even in terms of second order consequences and maybe figuring out how to get nearly all of what you want with just two wishes, so you have a safety valve of sorts with with number three? Nice!
Then you just need to find a genie, even an insane or half evil genie that can do almost anything?
One possibility is that no one will have built, or wanted to build a half insane genie that could easily kill the person holding the lamp. They will have assumed that The Goal can be discussed later, because surely the goal is pretty obvious? Its just good stuff, like what everyone wants for everyone.
So they won't have built a tiny little engine of pure creative insanity, they will have tried to build something that can at least be told what to do:
But then, the people who came up with a framework for thinking about the goals, and reconciling the possibility of contradictions or tradeoffs in the goals (in various clever ways (under extreme pressure of breakdown due to extremely creative things happening very quickly)) can say "I would like one of those 'Do Anything Machines' please, and I have a VERY LARGE VERY THOUGHTFUL WISH".
But in fact, if a very large and very thoughtful wish exists, you might safely throw away the philosophy stuff in the Do Anything Machine, why not get one, then tear out the Capability Robustness part, and just use THAT as the genie that tries to accomplish The Goal?
The danger might be that maybe you can't just tear the component out of the Do Anything Machine and still have it even sorta work? Or maybe by the end of working out the wish, it will turn out that there are categorically different kinds of genies and you need a specific reasoning or optimizing strategy to ensure that the wish (even a careful one that accounts for many potential gotchas) actually works out. Either getting a special one or tearing one out of the Do Anything Machine could work here:

If I was going to say some "and then" content here, based on this framing...
What if we didn't just give the "Do Anything Machine" a toy example of a toy alignment problem and hope it generalizes: what if we gave it "The Thoughtful Wish" as the training distribution to generalize?
Or (maybe equivalently, maybe not) what if "The Thoughtful Wish" was given a genie that actually didn't need that much thoughtfulness as its "optimizer" and so... is that better?
Personally, I see a Do Anything Machine and it kinda scares me. (Also, I hear "alignment" and think "if orthogonality is actually true, then you can align with evil as easily as with good, so wtf, why is there a nazgul in the fellowship already?")
And so if I imagine this instrument of potentially enormous danger being given a REALLY THOUGHTFUL GOAL then it seems obviously more helpful than if it was given a toy goal with lots of reliance on the "generalization" powers... (But maybe I'm wrong: see below!)
I don't have any similar sense that The Thoughtful Wish is substantially helped by using this or that optimization engine, but maybe I'm not understanding the idea very well.
For all of my understanding of the situation, it could be that if you have TWO non-trivial philosophical systems for reasoning about creative problem solving, and they interact... then maybe they... gum each other up? Maybe they cause echoes that resonate into something destructive? It seems like it would depend very very very much on the gears level view of both the systems, not just this high level description? Thus...
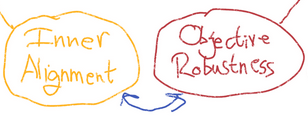
To the degree to which "Inner Alignment" and "Objective Robustness" are the same, or work well together, I think that says a lot. To the degree that they are quite different... uh...
Based on this diagram, it seems to me like they are not the same, because it kinda looks like "Inner Alignment" is "The Generalization Problem for only and exactly producing a Good AGI" whereas it seems like "Objective Robustness" would be able to flexibly generalize many many other goals that are... less obviously good?
So maybe Inner Alignment is a smaller and thus easier problem?
On the other hand, sometimes the easiest way to solve a motivating problem is to build a tool that can solve any problem that's vaguely similar (incorporating and leveraging the full generality of the problem space directly and elegantly without worrying about too many weird boundary conditions at the beginning) and then use the general tool to loop back and solve the motivating problem as a happy little side effect?
I have no stake in this game, except the obvious one where I don't want to be ground up into fuel paste by whatever thing someone eventually builds, but would rather grow up to be an angel and live forever and go meet aliens in my pet rocket ship (or whatever).
Hopefully this was helpful? <3
Maybe a very practical question about the diagram: is there a REASON for there to be no "sufficient together" linkage from "Intent Alignment" and "Robustness" up to "Behavioral Alignment"?
The ABSENCE of such a link suggests that maybe people think there WOULD be destructive interference? Or maybe the absence is just an oversight?
Maybe a very practical question about the diagram: is there a REASON for there to be no "sufficient together" linkage from "Intent Alignment" and "Robustness" up to "Behavioral Alignment"?
Leaning hard on my technical definitions:
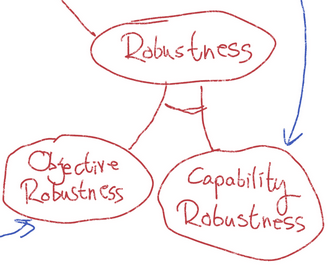
- Robustness: Performing well on the base objective in a wide range of circumstances.
- Intent Alignment: A model is intent-aligned if it has a mesa-objective, and that mesa-objective is aligned with humans. (Again, I don't want to get into exactly what "alignment" means.)
These two together do not quite imply behavioral alignment, because it's possible for a model to have a human-friendly mesa-objective but be super bad at achieving it, while being super good at achieving some other objective.
So, yes, there is a little bit of gear-grinding if we try to combine the two plans like that. They aren't quite the right thing to fit together.
It's like we have a magic vending machine that can give us anything, and we have a slip of paper with our careful wish, and we put the slip of paper in the coin slot.
That being said, if we had technology for achieving both intent alignment and robustness, I expect we'd be in a pretty good position! I think the main reason not to go after both is that we may possibly be able to get away with just one of the two paths.
Intent Alignment: A model is intent-aligned if it has a mesa-objective, and that mesa-objective is aligned with humans. (Again, I don't want to get into exactly what "alignment" means.)
This path apparently implies building goal-oriented systems; all of the subgoals require that there actually is a mesa-objective.
I pretty strongly endorse the new diagram with the pseudo-equivalences, with one caveat (much the same comment as on your last post)... I think it's a mistake to think of only mesa-optimizers as having "intent" or being "goal-oriented" unless we start to be more inclusive about what we mean by "mesa-optimizer" and "mesa-objective." I don't think those terms as defined in RFLO actually capture humans, but I definitely want to say that we're "goal-oriented" and have "intent."
But the graph structure makes perfect sense, I just am doing the mental substitution of "intent alignment means 'what the model is actually trying to do' is aligned with 'what we want it to do'." (Similar for inner robustness.)
However, I'm not confident that the details of Evan's locutions are quite right. For example, should alignment be tested only in terms of the very best policy?
I also don't think optimality is a useful condition in alignment definitions. (Also, a similarly weird move is pulled with "objective robustness," which is defined in terms of the optimal policy for a model's behavioral objective... so you'd have to get the behavioral objective, which is specific to your actual policy, and find the actually optimal policy for that objective, to determine objective robustness?)
I find myself thinking that objective robustness is actually what I mean by the inner alignment problem. Abergal voiced similar thoughts. But this makes it seem unfortunate that "inner alignment" refers specifically to the thing where there are mesa-optimizers. I'm not sure what to do about this.
Yeah, I think I'd also wish we could collectively agree to redefine inner alignment to be more like objective robustness (or at least be more inclusive of the kinds of inner goals humans have). But I've been careful not to use the term to refer to anything except mesa-optimizers, partially in order to be consistent with Evan's terminology, but primarily not to promote unnecessary confusion with those who strongly associate "inner alignment" with mesa-optimization (although they could also be using a much looser conception of mesa-optimization, if they consider humans to be mesa-optimizers, in which case "inner alignment" pretty much points at the thing I'd want it to point at).
I pretty strongly endorse the new diagram with the pseudo-equivalences, with one caveat (much the same comment as on your last post)... I think it's a mistake to think of only mesa-optimizers as having "intent" or being "goal-oriented" unless we start to be more inclusive about what we mean by "mesa-optimizer" and "mesa-objective." I don't think those terms as defined in RFLO actually capture humans, but I definitely want to say that we're "goal-oriented" and have "intent."
But the graph structure makes perfect sense, I just am doing the mental substitution of "intent alignment means 'what the model is actually trying to do' is aligned with 'what we want it to do'." (Similar for inner robustness.)
I too am a fan of broadening this a bit, but I am not sure how to.
I didn't really take the time to try and define "mesa-objective" here. My definition would be something like this: if we took long enough, we could point to places in the big NN (or whatever) which represent goal content, similarly to how we can point to reward systems (/ motivation systems) in the human brain. Messing with these would change the apparent objective of the NN, much like messing with human motivation centers.
I agree with your point about using "does this definition include humans" as a filter, and I think it would be easy to mess that up (and I wasn't thinking about it explicitly until you raised the point).
However, I think possibly you want a very behavioral definition of mesa-objective. If that's true, I wonder if you should just identify with the generalization-focused path instead. After all, one of the main differences between the two paths is that the generalization-focused path uses behavioral definitions, while the objective-focused path assumes some kind of explicit representation of goal content within a system.
I didn't really take the time to try and define "mesa-objective" here. My definition would be something like this: if we took long enough, we could point to places in the big NN (or whatever) which represent goal content, similarly to how we can point to reward systems (/ motivation systems) in the human brain. Messing with these would change the apparent objective of the NN, much like messing with human motivation centers.
This sounds reasonable and similar to the kinds of ideas for understanding agents' goals as cognitively implemented that I've been exploring recently.
However, I think possibly you want a very behavioral definition of mesa-objective. If that's true, I wonder if you should just identify with the generalization-focused path instead. After all, one of the main differences between the two paths is that the generalization-focused path uses behavioral definitions, while the objective-focused path assumes some kind of explicit representation of goal content within a system.
The funny thing is I am actually very unsatisfied with a purely behavioral notion of a model's objective, since a deceptive model would obviously externally appear to be a non-deceptive model in training. I just don't think there will be one part of the network we can point to and clearly interpret as being some objective function that the rest of the system's activity is optimizing. Even though I am partial to the generalization focused approach (in part because it kind of widens the goal posts with the "acceptability" vs. "give the model exactly the correct goal" thing), I still would like to have a more cognitive understanding of a system's "goals" because that seems like one of the best ways to make good predictions about how the system will generalize under distributional shift. I'm not against assuming some kind of explicit representation of goal content within a system (for sufficiently powerful systems); I'm just against assuming that that content will look like a mesa-objective as originally defined.
Seems fair. I'm similarly conflicted. In truth, both the generalization-focused path and the objective-focused path look a bit doomed to me.
So, for example, this claims that either intent alignment + objective robustness or outer alignment + robustness would be sufficient for impact alignment.
Shouldn’t this be “intent alignment + capability robustness or outer alignment + robustness”?
Btw, I plan to post more detailed comments in response here and to your other post, just wanted to note this so hopefully there’s no confusion in interpreting your diagram.
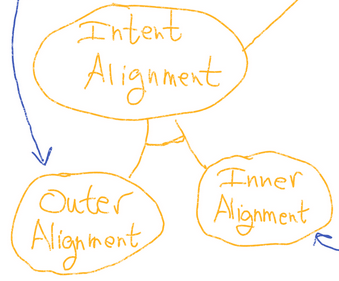
I've been poking at Evan's Clarifying Inner Alignment Terminology. His post gives two separate pictures (the objective-focused approach, which he focuses on, and the generalization-focused approach, which he mentions at the end). We can consolidate those pictures into one and-or graph as follows:
And-or graphs make explicit which subgoals are jointly sufficient, by drawing an arc between those subgoal lines. So, for example, this claims that intent alignment + capability robustness would be sufficient for impact alignment, but alternatively, outer alignment + robustness would also be sufficient. I've also added colors to make it a bit clearer.
The red represents what belongs entirely to the generalization-focused path. The yellow represents what belongs entirely to the objective-focused path. The blue represents everything else. (In this diagram, all the blue is on both paths, but that will not be the case in my next diagram.)
Note, in particular, that both paths seek outer alignment + objective robustness + capability robustness. According to the above picture, the disagreement between the two paths is only one of which of these sub-goals are better grouped together.
But this doesn't seem to actually be true. Objective Robustness and Inner Alignment Terminology points out that, really, the two approaches want to define some of the terminology differently. My previous post on the subject suggests even more differences. Putting these things together, and with some other revisions, I suggest this revised joint graph:
The and-or graph here has been supplemented with double-headed arrows, which indicate a looser relationship of pseudo-equivalence (more on this later).
Definitions:
Yellow Lines:
These lines represent the objective-centric approach. I think this rendering is more accurate than Evan's, primarily because my definition of intent alignment seems truer to Paul's original intention, and secondarily because inner alignment and outer alignment now form a nice pair.
This path apparently implies building goal-oriented systems; all of the subgoals require that there actually is a mesa-objective. In contrast, I think researchers who identify with this path probably don't all think the end result would necessarily be goal-oriented. For example, my impression of what people mean by "solving the inner alignment problem" includes building systems which robustly avoid having inner optimizers at all. This is not well-represented by the proposed graph.
We could re-define "inner alignment" to mean "the mesa-objective aligns with the base objective, or the system lacks any mesa-objective" -- but this includes a lot of dumb things under "inner aligned", which seems intuitively wrong.
A closer term is acceptability, which could plausibly be defined as "not actively pursuing a misaligned goal". However, I was not sure how to put anything like this into the graph in a nice way.
Red Lines:
These lines represent the generalization-focused approach.
This approach has some distinct advantages over the objective-focused approach. First, it does not assume the existence of inner optimizers at any point. It is possible that this approach could succeed without precisely defining "inner optimizer", identifying mesa-objectives and checking their alignment, or anything like that. Second, this approach can stand on the shoulders of existing statistical learning theory. If the whole problem boils down to generalization guarantees, then perhaps we just need to advance work on the same kinds of problems which machine learning has faced since its inception.
A subtlety here is that the base objective matters in two different ways. For "on-distribution alignment", we only care about how the base objective performs on the training data. This makes sense: that's the only way it effects training, so why would we care about correctly specifying outer alignment off-distribution? Instead, we rely on generalization to specify that part correctly. This seems like an advantage to the approach, because it greatly reduces the outer alignment problem.
However, objective robustness also depends on the base objective, and specifically depends on the off-distribution behavior of the base objective. This reflects the fact that to generalize correctly, the system does need to get information about the off-distribution base objective somehow. But how? In prosaic AI, only on-distribution behavior of the loss function can influence the end result.
I can see a few possible responses here.
Response #2 is consistent with how the generalization-focused path has been drawn by others; IE, it includes inner alignment as a subgoal of objective robustness. However, including this fully in the generalization-focused path seems unfortunate to me, because it adds mesa-objectives as a necessary assumption (since inner alignment requires them). Perhaps dealing directly with mesa-objectives is unavoidable. However, I would prefer to be agnostic about that for the time being.
EDIT:
I now think (to fix the above-mentioned problem, and to represent Rohin's view more accurately) we should re-define objective robustness as follows:
Objective Robustness: The behavioral objective generalizes acceptably.
The notion of "acceptable" is left purposefully open, but it should have two desirable properties:
Blue Lines:
Inner Robustness and Capability Robustness
Inner robustness implies capability robustness, because we know there's a goal which the system performs well on in a broad variety of circumstances. (Inner robustness just tells us a bit more about what that goal is, while capability robustness doesn't care.)
Capability robustness sort of implies inner robustness, if we assume a degree of agency: it would be pretty strange for the system to robustly pursue some other goal than its mesa-objective.
However, these implications require the presence of an inner optimizer. In particular, capability robustness obviously won't imply inner robustness in the absence of one of those.
Inner Alignment and Objective Robustness
Evan argued that inner alignment implies objective robustness. This argument requires that the agent is capable enough that its behavioral objective will match its mesa-objective, even under distributional shift.
We could also argue in the other direction: if something is behaviorally aligned with the base objective in a broad variety of circumstances, then (again assuming sufficient agency), surely it must not have a misaligned objective.
Again, these implications only make sense if there is a mesa-objective.
On-Distribution Alignment and Outer Alignment
Outer alignment implies on-distribution alignment trivially. On-distribution doesn't imply outer alignment by any means, but the pseudo-equivalence here is because outer alignment doesn't matter beyond the influence of the base objective on training; so, at least for prosaic AI, outer alignment shouldn't matter beyond on-distribution alignment.
Equating Pseudo-Equivalences
If we collapse all the pseudo-equivalent subgoals, we get an and-or graph which looks quite similar to the one we started out with:
This makes clear that both approaches have an "inner alignment type thing", an "outer alignment type thing", and a "capability type thing"; they just define these things differently:
This may be an easier way to remember my larger graph.
Other remarks:
Definition of "Alignment"
I've used the term "aligned" in several definitions where Evan used more nuanced phrases. For example, inner alignment:
Evan's definition seems more nuanced and useful. It puts some gears on the concept of alignment. It averts the mistake "aligned means equal" (if humans want to drink coffee, that should not imply that aligned robots want to drink coffee). It captures the idea that goal alignment has to do with high levels of performance (we don't want to label something as misaligned just because it makes dumb mistakes).
However, I'm not confident that the details of Evan's locutions are quite right. For example, should alignment be tested only in terms of the very best policy? This seems like a necessary condition, but not sufficient. If behavior is severely misaligned even for some very very high-performance policies (but technically sub-optimal), then the alignment isn't good enough; we don't expect training to find the very best policy.
So, I think it better to remain somewhat ambiguous for this post, and just say "aligned" without going further.
Other Nuances
Note that with my re-definition of "objective robustness", the generalization-focused path now implies achieving a weaker kind of alignment: the objective-focused approach achieves what we might call strong alignment, where the system is robustly pursuing aligned goals. The generalization-focused approach will be weaker (depending on how exactly "acceptability" gets defined), only guaranteeing that the resulting system doesn't do something terrible. (This weaker form of alignment seems very reasonable to me.)
This means we can split the top bubble into objective/generalization -focused versions, like the others. If we really want, we can also come up with split definitions of "robustness" and "intent alignment", so that the whole graph gets split, although this doesn't seem particularly useful.
The "task AI vs goal-directed AI" distinction deserves a mention. To some extent, the objective-focused approach is all about goal-directed AI, while the generalization-focused approach remains more agnostic. However, it could be that task-based systems still have mesa-objectives (EG "do what the user says"), just myopic ones. Part of inner alignment is then to ensure myopia.
Meta-thoughts on the graph/terminology.
Generally, I felt like if I had chosen more things to be careful about, I could have made the graph three times as big. It's tempting to try and map out all possible important properties and all possible approaches. However, the value of a map like this rapidly diminishes as the map gets larger. Which things to make perfectly clear vs muddy is a highly subjective choice. I would appreciate feedback on the choices I made, as this will inform my write-up-to-come. (This post will resemble the first major section of that write-up.)
Also, I'm not very committed to the terms I chose here. EG, using "behavioral alignment" rather than "impact alignment". I welcome alternate naming schemes.
I find myself thinking that objective robustness is actually what I mean by the inner alignment problem. Abergal voiced similar thoughts. But this makes it seem unfortunate that "inner alignment" refers specifically to the thing where there are mesa-optimizers. I'm not sure what to do about this.